Mathematisches Pendel als Taktmechanismus¶
Ein einführendes Beispiel
Aufgabe: Mit Hilfe eines Pendels soll ein Taktmechanismus zu einer vorgegebenen Taktzeit \(T^*>0\) realisiert werden. Zu bestimmen ist daher die erforderliche Anfangsauslenkung zu einer gegebenen Schwingungsdauer \(T^*\). Die Schwingungsdauer \(T\) bezeichnet die Zeit, welches das Pendel benötigt um wieder in die Ausgangslage zurück zu schwingen.
Mit Hilfe des Anfangswertproblems \begin{equation}\label{eq:modellbeispiel}\begin{split} \ddot{\phi}(t) & = - \frac{g}{l}\cdot \sin(\phi(t))\\ \phi(0) & = \phi_0\quad\text{und}\quad \dot{\phi}(0) = 0 \end{split}\end{equation} können wir die Bewegung des Pendels mathematisch modellieren und beschreiben.
Die Differentialgleichung kann nicht geschlossen gelöst werden. Daher werden numerische Methoden für die Berechnung von \(\phi(t)\) benötigt. Für kleine Auslenkungen kann die Näherung
benutzt werden. Das vereinfachte Modell lautet in dem Fall \begin{equation}\label{eq:einfachesModell}\begin{split} \ddot{\phi}(t) & = - \frac{g}{l}\cdot \phi(t)\\ \phi(0) & = \phi_0\quad\text{und}\quad \dot{\phi}(0) = 0. \end{split}\end{equation} Damit wird jedoch ein weiterer systematischer Fehler eingeführt, ein unter Umständen sehr wesentlicher Modellfehler: Die Lösung des vereinfachten Modells ist gegeben durch
Offensichtlich scheitert hier das Vorhaben die Taktzeit über die Anfangsauslenkung einzustellen. Die Taktzeit ist in dem Fall unabhängig von der Anfangsauslenkung!
1. Schritt¶
Numerische Lösung der nichtlinearen DGL 2. Ordnung
Um numerisch rechnen zu können, müssen sämtliche Parameter gegeben sein. Wir setzen daher
[1]:
g = 9.81
l = 0.6
[2]:
import sys
sys.path.append('../numerikODE/')
from odeSolvers import classicRungeKutta
import numpy as np
import matplotlib.pyplot as plt
import time
und definieren eine Funktion, welche für
einen gegebenen Startwert \(\varphi(0) = \varphi_0\)
und der Startgeschwindigkeit \(\dot{\varphi}(0) = 0\)
eine Lösung berechnet:
[3]:
def f(t,phi):
return np.array([phi[1], -g/l*np.sin(phi[0])])
def phipendel(phi0):
t,phi = classicRungeKutta(40,1e-2,np.array([phi0,0.]),f)
return lambda s: np.interp(s,t,phi[:,0])
Damit können wir Lösungen für gegegebene \(\varphi_0\) betrachten:
[4]:
tp = np.linspace(0,10,300)
[plt.plot(tp,phipendel(phii)(tp), label=r'$\varphi_0=$'+str(np.round(phii,3))) for phii in [0.1,1,np.pi-0.01]]
plt.legend()
plt.grid(); plt.xlabel(r'$t$'); plt.ylabel(r'$\varphi(t)$')
plt.show()
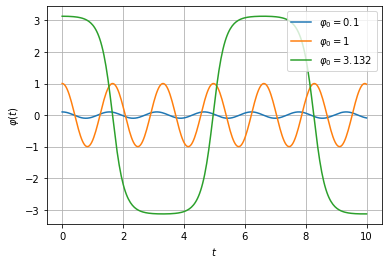
2. Schritt¶
Berechnen der Periodizität :math:`T`
Wir berechnen wiederum numerisch den Nulldurchgang von \(\varphi(t)\) um daraus die Periodizität zu berechnen.
[5]:
from scipy.optimize import root
[6]:
sol=root(phipendel(0.1),0.3)
sol
[6]:
fjac: array([[-1.]])
fun: array([-9.10729825e-18])
message: 'The solution converged.'
nfev: 8
qtf: array([9.10729825e-18])
r: array([0.])
status: 1
success: True
x: array([0.38871586])
[7]:
plt.plot(tp, phipendel(0.1)(tp))
plt.axvline(sol.x,c='orange')
plt.grid(); plt.xlabel(r'$t$'); plt.ylabel(r'$\varphi(t)$')
plt.show()
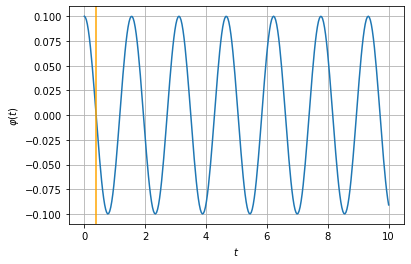
Wir erhalten daher für den Startwinkel \(\varphi_0 = 0.1\) eine Periodizität von
[8]:
4*sol.x[0]
[8]:
1.554863436589423
Nun interessiert uns diese Abhängigkeit, daher \(T(\varphi_0)\):
[9]:
cpustart = time.time()
phi0s = np.linspace(0.01,np.pi-0.01,300)
Ts = np.array([4*root(phipendel(phi0),0.5).x[0] for phi0 in phi0s])
cpuend = time.time()
print('cpu-time:', cpuend-cpustart)
cpu-time: 24.756715059280396
Die Rechenzeit ist schon ziemlich lange für diese einfache Parameterstudie.
[10]:
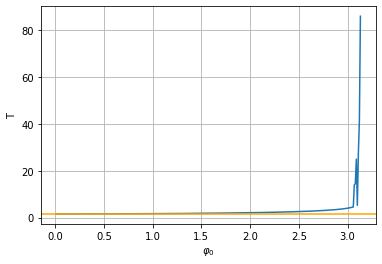
plt.plot(phi0s,Ts)
plt.xlabel(r'$\varphi_0$'); plt.ylabel('T'); plt.grid()
plt.axhline(2*np.pi/np.sqrt(g/l),c='orange');
plt.show()
[11]:
plt.plot(phi0s,Ts)
plt.xlabel(r'$\varphi_0$'); plt.ylabel('T'); plt.grid()
plt.ylim(0,10); plt.axhline(2*np.pi/np.sqrt(g/l),c='orange');
plt.show()
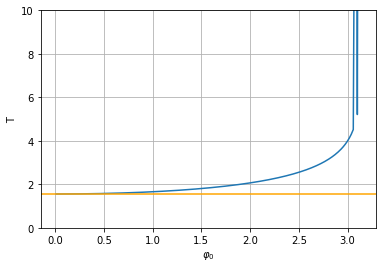
Das Verfahren scheint bis für \(\varphi_0=3\) zu funktionieren.
Für \(\varphi_0>3\) wird das Verfahren instabil.
Ganz offensichtlich ist die Periodizität vom Startwinkel abhängig.
Für einen Startwinkel \(\varphi_0 \to \pi\) muss die Periodizität \(T \to \infty\) streben.
3. Schritt¶
Effektiv gesuchte Abhängigkeit
Die Lösung im 2. Schritt ist soweit so gut. Uns interessiert aber die Umkehrfunktion:
Für eine gegebene Periodizität \(T\) soll der Startwinkel berechnet werden!
Man könnte nun wiederum einen nichtlinearen Solver belästigen. Aber eventuell reicht auch schon eine geeignetere graphische Darstellung der Lösung, durch Vertauschen der Achsen:
[12]:
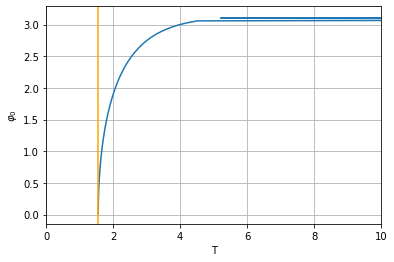
plt.plot(Ts, phi0s)
plt.ylabel(r'$\varphi_0$'); plt.xlabel('T'); plt.grid()
plt.xlim(0,10); plt.axvline(2*np.pi/np.sqrt(g/l),c='orange');
plt.show()
4. Schritt¶
Effizientes, stabiles Verfahren
Die vorgestellte Brutforce Methodik ist ganz offensichtlich nicht effizient:
es werden für kleine Startwinkel \(\varphi_0\) viel zu viele Zeitschritte berechnet,
es wird der falsche Nulldurchgang für die Berechnung Periodizität gefunden.
Lösung: Wir berechnen daher die Lösung der DGL nur noch bis zum Nulldurchgang und geben diese Zeit als Rückgabewert.
[13]:
cpustart = time.time()
Ts2 = np.array([4*classicRungeKutta(40,1e-2,np.array([phi0,0.]),f,trigger=0) for phi0 in phi0s])
cpuend = time.time()
print('cpu-time:', cpuend-cpustart)
cpu-time: 0.36338162422180176
[14]:
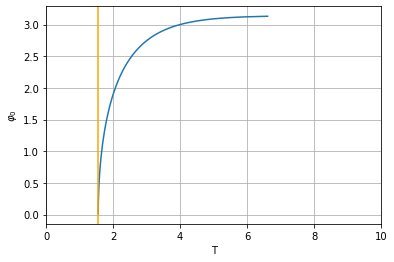
plt.plot(Ts2, phi0s)
plt.ylabel(r'$\varphi_0$'); plt.xlabel('T'); plt.grid()
plt.xlim(0,10); plt.axvline(2*np.pi/np.sqrt(g/l),c='orange');
plt.show()
Fazit:
Numerik ist mehr als einfach nur rechnen.
Mathematische Beschreibung basiert auf Modelle
Modellfehler müssen beachtet werden
ist das Modell zu trivial, ist evtl. keine Aussage möglich
Verfahren müssen stabil sein
Brutforce kann teuer (0.4s vs 24s) und instabil sein!
Ziel dieses Moduls:
Einen Einblick in das wissenschaftliche Rechnen (Scientific Computation) zu geben.
Für Problemstellungen sensibilisieren.
\(\Rightarrow\) Wissenschaftliches Rechnen ist integraler Bestandteil des Ingenieur Alltags.
[ ]: