Finite Differenzen Methode

Wir betrachten das Randwertproblem \begin{equation}\label{eq:exmprandwertproblem}\begin{split} -u''(x) & = f(x)\quad\text{für}\ x\in (0,1)\\ u(0) & = 0\\ u(1) & = 0. \end{split}\end{equation}

Mit \(f(x) = 1\)

Die analytische Lösung folgt leicht mittels zweimaliges Integrieren

\[u(x) = -\frac{1}{2} x (x-1).\]

import numpy as np
import matplotlib.pyplot as plt

Numerische Lösung des Randwertproblems

# Rechteseite
def f(x):
    return np.ones_like(x)

# Randbedingungen
uR = 0
uL = 0

def uanalytisch(x):
    return -0.5*x*(x-1)

Diskretisierung des Intervall \([0,1]\) mit äquidistanten Stützpunkte

n = 5
x = np.linspace(0,1,n+1)
h = 1/n

In Matrixschreibweise folgt für das diskrete System (vgl. Skript)

\[\begin{split}\underbrace{\begin{pmatrix} 2 & -1 & 0 & \ldots & 0 \\ -1 & 2 & \ddots & \ddots & \vdots\\ 0 & \ddots & \ddots & & 0\\ \vdots & \ddots & & 2 & -1 \\ 0 & \ldots & 0 & -1 & 2 \end{pmatrix}}_{\displaystyle = A}\cdot \underbrace{\begin{pmatrix} u_1\\ u_2\\\vdots\\u_{n-2} \\u_{n-1} \end{pmatrix}}_{\displaystyle = u} = \underbrace{\begin{pmatrix} \Delta x^2 + u_0\\ \Delta x^2\\ \vdots\\ \Delta x^2\\ \Delta x^2 + u_n\\ \end{pmatrix}}_{\displaystyle = b}\end{split}\]

Gesucht ist daher der Vektor \(u\) des linearen Gleichungssystems

\[A\cdot u = b\]

A = np.diag(2*np.ones(n-1)) - np.diag(np.ones(n-2),1) - np.diag(np.ones(n-2),-1)

b = h**2*f(x[1:-1]) # die Funktion wird bei den inneren Punkte ausgewertet
b[0] += uL           # rechter Randwert
b[-1] += uR          # linker Randwert

# import lu decomposition from scipy
from scipy.linalg import lu, solve_triangular

P,L,R = lu(A,)

Wir lösen das faktorisierte Gleichungssystem durch Vor- / Rückwärtseinsetzen:

\[L\cdot \underbrace{R\cdot u}_{z} = P^T\cdot b\]

Daher lösen wir mittels Vorwärtseinsetzen zuerst die Gleichung

\[L\cdot z = P^T\cdot b\]

und danach mit Rückwärtseinsetzen

\[R\cdot u = z.\]

Bemerkung: Vorsicht im Skript benutzen wir \(L\cdot R = P\cdot A\). Die Aussage ist, dass eine Permutationsmatrix \(P\) existiert so, dass \(P\cdot A = L\cdot R\) gilt. Numpy und Scipy liefern jedoch \(A = P\cdot L\cdot R\), wobei jeweilen \(P\) bis auf das transponierte identisch sind.

Die Matrixmultiplikation der Permutation kann vermieden werden:

ind = []
for i in range(n-1):
    j = 0
    while P[j,i] == 0:
        j += 1
    ind.append(j)
ind = np.array(ind)

Damit haben wir die Reihenfolge der Zeilen im Vektor ind gespeichert.

Vorwärtseinsetzen:

z = solve_triangular(L,b[ind],lower=True)

Rückwärtseinsetzen:

u = np.zeros_like(x)
u[0] = uL
u[-1] = uR
u[1:-1] = solve_triangular(R,z)

Visualisierung der Lösung

plt.plot(x,u,label='FDM Lösung')
xp = np.linspace(0,1,300)
plt.plot(xp, uanalytisch(xp), label='exakte Lösung')
plt.xlabel('$x$')
plt.ylabel('$u,u_h$')
plt.legend()
plt.grid()
plt.show()

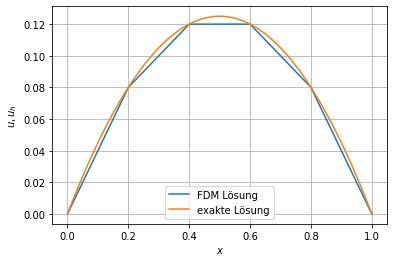
Das Ergebniss lässt sich selber bei nur fünf Intervalle sehen.

Konvergenz

Um die Konvergenz zu diskutieren packen wir alles in eine Funktion.

def fdmLoeser(n):
    x = np.linspace(0,1,n+1)
    h = 1/n
    A = np.diag(2*np.ones(n-1)) - np.diag(np.ones(n-2),1) - np.diag(np.ones(n-2),-1)
    b = h**2*f(x[1:-1]) # die Funktion wird bei den inneren Punkte ausgewertet
    b[0] += uL           # rechter Randwert
    b[-1] += uR          # linker Randwert
    P,L,R = lu(A,)
    ind = []
    for i in range(n-1):
        j = 0
        while P[j,i] == 0:
            j += 1
        ind.append(j)
    ind = np.array(ind)
    z = solve_triangular(L,b[ind],lower=True)
    u = np.zeros_like(x)
    u[0] = uL
    u[-1] = uR
    u[1:-1] = solve_triangular(R,z)
    return x,u

err = []
h = []
for n in 10**np.arange(1,5):
    x,u = fdmLoeser(n)
    h.append(1/n)
    err.append(np.linalg.norm(u-uanalytisch(x),ord=np.inf))
err = np.array(err)
h = np.array(h)

plt.loglog(h,err)
plt.grid()
plt.xlabel('$\Delta x$')
plt.ylabel('$\|e_h\|_{2,h}$')
plt.show()

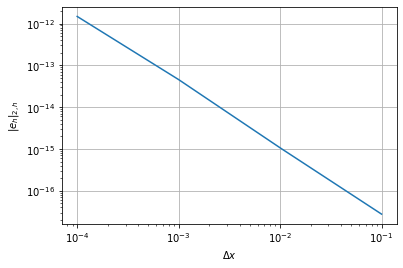
Für das Beispiel können wir eine interessante Eigenschaft der Gleichung beobachten, auf die wir später eingehen: In diesem Beispiel liefert die FDM unabhängig von der Schrittweite die exakte Lösung! Dass der Fehler zunimmt liegt am numerischen Rundungsfehler, welche in dem Fall für den Fehler verantwortlich sind.

Weiteres Beispiel

Um eine vernünftige Konvergenzordnung beobachten zu können, wählen wir eine andere rechte Seite \(f(x)\) der Differentialgleichung. Sei \(f(x)\) gegeben durch

\[f(x) = \sin(2\pi x)^2.\]

def f(x):
    return np.sin(2*np.pi*x)**2

Mittels Integration können wir wiederum die exakte Lösung analytisch berechnen.

def uanalytisch(x):
    return (1 + 8*np.pi**2*x - 8*np.pi**2*x**2 - np.cos(4*np.pi*x))/(32.*np.pi**2)

err = []
h = []
for n in 10**np.arange(1,4):
    x,u = fdmLoeser(n)
    h.append(1/n)
    err.append(np.linalg.norm(u-uanalytisch(x),ord=np.inf))
err = np.array(err)
h = np.array(h)

plt.loglog(h/h[0],err/err[0])
plt.grid()
plt.xlabel('$\Delta x$')
plt.ylabel('$\|e_h\|_{2,h}$')
plt.show()

Es kann gezeigt werden, dass unter der Voraussetzung \(u(x)\in C^4([0,1])\)

\[\|e_h\|_{2,h} \le \frac{1}{48} C h^2\]

gilt, wobei

\[C = \|u^{(4)}(x)\|_{\infty}.\]

Der Fehler geht daher quadratisch gegen 0 für \(\Delta x \to 0\), wie wir im Beispiel beobachten können.