Numerisches Beispiel zur Konvergenzordnung¶
[1]:
import numpy as np
import matplotlib.pyplot as plt
Eine konvergente Folge \(\{x_k\}_{k\in\mathbb{N}} \subset \mathbb{R}^n\) mit Grenzwert \(x^*\) hat die Konvergenzordnung \(p\), falls für ein \(k_0\in\mathbb{N}\)
\[\|x_{k+1}-x^*\| \le c \| x_k - x^*\|^p\]
für alle \(k\ge k_0\) gilt, wobei
\[0 < c < 1 \quad\text{falls}\quad p=1.\]
Wir betrachten das numerische Beispiel mit
[2]:
c = 0.1
und
\[\epsilon_k = \|x_k - x^*\|\]
mit
[3]:
epsilon0 = 1
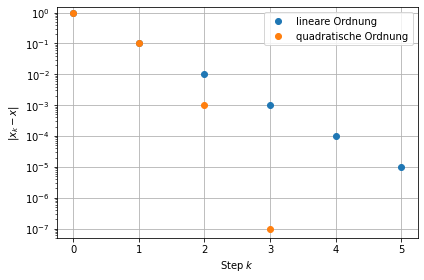
Ausgehend vom initialen Fehler \(\varepsilon_0\) berechnen wir die Konvergenz unter der Annahme, dass für die Ungleichung die Gleichheit gilt
\[\varepsilon_{k+1} = c\, \varepsilon_k.\]
[4]:
eps1 = [epsilon0]
eps2 = [epsilon0]
for k in range(5):
# lineare Ordnung
nextepsilon1 = c*eps1[-1]**1
eps1.append(nextepsilon1)
# quadratische Ordnung
nextepsilon2 = c*eps2[-1]**2
eps2.append(nextepsilon2)
[5]:
plt.semilogy(eps1,'o',label='lineare Ordnung')
plt.plot(eps2,'o',label='quadratische Ordnung')
plt.grid()
plt.ylim(5e-8,1.5)
plt.legend()
plt.xlabel('Step $k$')
plt.ylabel(r'$\|x_k-x\|$')
plt.tight_layout()
#plt.gca().set_aspect(.75)
plt.savefig('VergleichKonvergenzOrdnung.pdf')
plt.show()
[ ]: