Idee der Householdertransformation¶
[1]:
import matplotlib.pyplot as plt
import numpy as np
from ipywidgets import interactive
from numpy.linalg import norm
[2]:
np.set_printoptions(precision=2,suppress=True)
Wir betrachten die Idee der Householdertransformation am Beispiel einer 2x2 Matrix:
[3]:
A0 = np.array([[1,7],[3,3]])
print(A0)
[[1 7]
[3 3]]
In einem ersten Schritt Betrachten wir die erste Spalte.
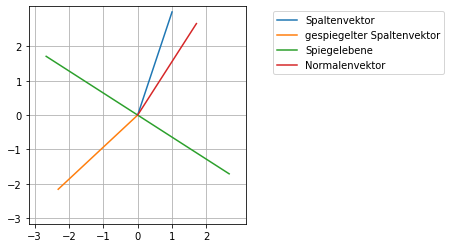
Gesucht ist daher eine geeignete Spiegelungsebene so, dass der erste Spaltenvektor zum \(\pm\) Einheitsvektor \(e_1\) gespiegelt wird.
[4]:
def HouseholderTransformation(w):
return np.eye(w.shape[0])-2*np.outer(w,w)/np.dot(w,w)
def normalVector(alpha):
return np.array([np.cos(alpha), np.sin(alpha)])
def tangentialVector(alpha):
return np.array([np.sin(alpha), -np.cos(alpha)])
[5]:
def f(alpha):
n = normalVector(alpha)
t = tangentialVector(alpha)
y = A0[:,0]
Hy = HouseholderTransformation(n).dot(y)
normy = np.sqrt(y.dot(y))
tpt = np.linspace(-normy,normy,2)
tpn = np.linspace(0,normy,2)
tpy = np.linspace(0,1,2)
plt.plot(tpy*y[0],tpy*y[1],label='Spaltenvektor')
plt.plot(tpy*Hy[0],tpy*Hy[1],label='gespiegelter Spaltenvektor')
plt.plot(tpt*t[0],tpt*t[1],label='Spiegelebene')
plt.plot(tpn*n[0],tpn*n[1],label='Normalenvektor')
plt.gca().set_aspect(1)
plt.legend(bbox_to_anchor=(1.1,1))
plt.grid()
plt.xticks(np.arange(-np.round(normy),np.round(normy)))
plt.yticks(np.arange(-np.round(normy),np.round(normy)))
plt.xlim(-normy,normy)
plt.ylim(-normy,normy)
plt.show()
f(1)
[6]:
interactive_plot = interactive(f, alpha=(-np.pi/2, np.pi/2,1e-3))
output = interactive_plot.children[-1]
output.layout.height = '350px'
interactive_plot
Gesucht ist daher der geeignete Normalenvektor so, dass der gespiegelte Spaltenvektor auf die \(e_1\) Achse zu liegen kommt.
Sei mit \(y\) der Spaltenvektor bezeichnet, so kann man zeigen (siehe Skript), dass der Vektor
die gewünschte Eigenschaft hat. Um Auslöschung in der Berechnung von \(w\) zu vermeiden, wählt man
mit
[7]:
def mysign(x): # numpy sign liefert 0 für 0
if x >= 0:
return 1
else:
return -1
Funktion für den n-dimensionalen Einheitsvektor
[8]:
def e(n):
return np.array([1]+[0 for k in range(n-1)])
Schrittweise QR-Zerlegung mit Hilfe der Householder-Transformation¶
Mit Hilfe der Householder-Transformation soll nun die Matrix \(A\) in eine orthogonale Matrix \(Q\) und reguläre obere Dreiecksmatrix \(R\) zerlegt werden.
Im Beispiel wählen wir eine beliebige Matrix \(A \in \mathbb{R}^{10\times5}\).
[9]:
A = np.array([[-1, 7, -8, -9, 6],
[-6, -8, 0, 3, 8],
[-4, -2, 8, 0, -2],
[-1, -9, 4, -8, 2],
[-3, -5, -5, 7, -4],
[-7, -4, 7, -1, 5],
[-9, -7, 6, -5, -8],
[-4, -3, -5, 3, -6],
[ 5, 7, 5, -4, -5],
[ 4, -6, -8, -2, -5]],dtype=float)
m,n = A.shape
print(m,n)
10 5
1. Spalte¶
[10]:
k = 0
Die Hyperebene ist definiert durch
[11]:
w = A[k:,k] + mysign(A[k,k])*norm(A[k:,k])*e(m-k)
Für die Householder-Transformationsmatrix angewand auf \(A\) erhalten wir
[12]:
Q1 = HouseholderTransformation(w)
A1 = Q1@A
In der ersten Spalte der Zwischenmatrix \(A_1\) stehen nun abgesehen vom ersten Eintrag Nullen:
[13]:
print(A1)
[[ 15.81 11.83 -6.51 -0.63 -1.26]
[ -0. -6.28 0.53 5.99 5.41]
[ -0. -0.85 8.35 1.99 -3.73]
[ -0. -8.71 4.09 -7.5 1.57]
[ -0. -4.14 -4.73 8.49 -5.3 ]
[ -0. -1.99 7.62 2.48 1.98]
[ -0. -4.42 6.8 -0.52 -11.89]
[ -0. -1.85 -4.65 4.99 -7.73]
[ 0. 5.56 4.56 -6.49 -2.84]
[ 0. -7.15 -8.35 -3.99 -3.27]]
2. Spalte¶
[14]:
k = 1
Die Hyperebene ist definiert durch
[15]:
w = A1[k:,k] + mysign(A1[k,k])*norm(A1[k:,k])*e(m-k)
wobei nun das letzte Resultat \(A_1\) benutzt wird. Die Householder-Transformationsmatrix wird nun nur auf die Submatrix von \(A_1\) angewand und in der Submatrix von \(A_1\) wiederum gespeichert:
[16]:
Q2 = HouseholderTransformation(w)
A1[k:,k:] = Q2@A1[k:,k:]
Die Dimension der zweiten Householder-Transformationsmatrix \(Q_2\) ist
[17]:
Q2.shape
[17]:
(9, 9)
In dem ersten beiden Spalte der Zwischenmatrix \(A_1\) steht:
[18]:
print(A1)
[[ 15.81 11.83 -6.51 -0.63 -1.26]
[ -0. 15.56 1.42 -1.83 3.08]
[ -0. 0. 8.39 1.69 -3.82]
[ -0. -0. 4.44 -10.62 0.64]
[ -0. 0. -4.57 7.01 -5.74]
[ -0. -0. 7.7 1.77 1.76]
[ -0. -0. 6.97 -2.1 -12.36]
[ -0. -0. -4.57 4.33 -7.93]
[ 0. -0. 4.33 -4.5 -2.25]
[ 0. 0. -8.06 -6.55 -4.03]]
3. - 5. Spalte¶
Wir automatisieren nun den Prozess und überschreiben die Submatrizen der Matrix \(A_1\) sukzessive:
[19]:
for k in range(2,n):
print('Spalte '+str(k+1))
w = A1[k:,k] + mysign(A1[k,k])*norm(A1[k:,k])*e(m-k)
Qk = HouseholderTransformation(w)
A1[k:,k:] = Qk@A1[k:,k:]
print(A1)
Spalte 3
[[ 15.81 11.83 -6.51 -0.63 -1.26]
[ -0. 15.56 1.42 -1.83 3.08]
[ -0. 0. -17.99 2.92 0.92]
[ -0. -0. 0. -10.41 1.44]
[ -0. 0. -0. 6.8 -6.56]
[ -0. -0. 0. 2.13 3.15]
[ -0. -0. 0. -1.78 -11.11]
[ -0. -0. -0. 4.11 -8.75]
[ 0. -0. 0. -4.29 -1.47]
[ 0. 0. -0. -6.93 -5.48]]
Spalte 4
[[ 15.81 11.83 -6.51 -0.63 -1.26]
[ -0. 15.56 1.42 -1.83 3.08]
[ -0. 0. -17.99 2.92 0.92]
[ -0. -0. 0. 15.68 -1.59]
[ -0. 0. -0. -0. -5.77]
[ -0. -0. 0. -0. 3.39]
[ -0. -0. 0. -0. -11.31]
[ -0. -0. -0. 0. -8.27]
[ 0. -0. 0. 0. -1.97]
[ 0. 0. -0. -0. -6.29]]
Spalte 5
[[ 15.81 11.83 -6.51 -0.63 -1.26]
[ -0. 15.56 1.42 -1.83 3.08]
[ -0. 0. -17.99 2.92 0.92]
[ -0. -0. 0. 15.68 -1.59]
[ -0. 0. -0. -0. 16.87]
[ -0. -0. 0. -0. -0. ]
[ -0. -0. 0. -0. 0. ]
[ -0. -0. -0. 0. -0. ]
[ 0. -0. 0. 0. 0. ]
[ 0. 0. -0. -0. 0. ]]
QR-Zerlegung¶
Wir berechnen nun alle Schritte in einer ‚for‘-Schlaufe und berechnen \(Q^T\) so, dass
gilt.
[20]:
A1 = A.copy()
QT = np.eye(m)
for k in range(0,n):
w = A1[k:,k] + mysign(A1[k,k])*norm(A1[k:,k])*e(m-k)
Qk = HouseholderTransformation(w)
A1[k:,k:] = Qk@A1[k:,k:]
Qkext = np.eye(m)
Qkext[k:,k:] = Qk
QT = Qkext@QT
Damit folgt
[21]:
Q = QT.T
R = A1
und
[22]:
A-Q@R
[22]:
array([[-0., 0., -0., 0., 0.],
[-0., -0., -0., 0., 0.],
[-0., 0., 0., -0., -0.],
[-0., -0., 0., 0., -0.],
[-0., 0., -0., 0., 0.],
[-0., 0., -0., -0., -0.],
[ 0., 0., -0., -0., 0.],
[-0., 0., -0., -0., -0.],
[ 0., 0., 0., 0., 0.],
[ 0., -0., -0., 0., -0.]])