Einstiegsbeispiel lineare Ausgleichsrechnung¶
[11]:
import numpy as np
import matplotlib.pyplot as plt
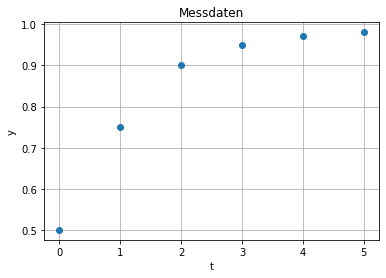
Gegeben seien die Messdaten
mit einer vermuteten Gesetzmässigkeit der Form
[12]:
t = np.arange(6)
y = np.array([1/2,3/4,9/10,19/20,33/34,51/52])
[13]:
plt.plot(t,y,'o')
plt.xlabel('t')
plt.ylabel('y')
plt.title('Messdaten')
plt.grid()
plt.show()
Systemmatrix¶
Die beiden Basisfunktionen sind gegeben durch
Sei
[14]:
def u1(t):
return 1/(1+t**2)
def u2(t):
return np.ones_like(t)
def u(t):
return np.array([u1(t), u2(t)]).T
Die Systemmatrix \(A\) ist somit gegeben durch
[15]:
A = u(t)
A
[15]:
array([[1. , 1. ],
[0.5 , 1. ],
[0.2 , 1. ],
[0.1 , 1. ],
[0.05882353, 1. ],
[0.03846154, 1. ]])
oder kompakt (np.broadcast_arrays gleicht beliebig viele Arrays gegeneinander ab):
[16]:
np.stack(np.broadcast_arrays(*[1/(1+t**2),1]),-1)
[16]:
array([[1. , 1. ],
[0.5 , 1. ],
[0.2 , 1. ],
[0.1 , 1. ],
[0.05882353, 1. ],
[0.03846154, 1. ]])
Im Skirpt wird als wichtiges Beispiel einer symmetrisch positiv definiten Matrix die Matrix
erwähnt, wobei die Spalten von \(A\) linear unabhängig sein müssen.
[17]:
A.T@A
[17]:
array([[1.3049395 , 1.89728507],
[1.89728507, 6. ]])
Der kleineste Eigenwert von \(A^T\cdot A\) ist gegeben durch
[18]:
from scipy.linalg import eigvals
# Berechnung der Eigenwerte
eig = eigvals(A.T@A)
np.real(eig)
[18]:
array([0.63409454, 6.67084496])
Im Beispiel ist wie zu erwarten, der kleinste Eigenwert strikt positiv:
[19]:
np.min(eig)
[19]:
np.complex128(0.6340945386372852+0j)
Bemerkung: Die Ansatz- oder Basisfunktionen müssen linearunabhängig sein. Ist dies nicht der Fall, bringen wir keine Mehrinformation ins System.
Es stellt sich die Frage: Wie macht sich das in der Numerik sichtbar?
Wir betrachten die Erweiterung unserer Ansatzfunktionen mit dem Vielfachen von \(u_1\):
[20]:
def v(t):
return np.array([u1(t), 2*u1(t), u2(t)]).T
Damit folgt die Systemmatrix
[21]:
A2 = v(t)
A2
[21]:
array([[1. , 2. , 1. ],
[0.5 , 1. , 1. ],
[0.2 , 0.4 , 1. ],
[0.1 , 0.2 , 1. ],
[0.05882353, 0.11764706, 1. ],
[0.03846154, 0.07692308, 1. ]])
Berechnet man wiederum die Matrix \(A_2^T\cdot A_2\):
[22]:
A2.T@A2
[22]:
array([[1.3049395 , 2.609879 , 1.89728507],
[2.609879 , 5.21975799, 3.79457014],
[1.89728507, 3.79457014, 6. ]])
und ihre Eigenwerte:
[23]:
np.real(eigvals(A2.T@A2))
[23]:
array([1.05129111e+01, 1.58767221e-16, 2.01178643e+00])
so ist der kleinste Eigenwert \(5\cdot 10^{-16}\), also numerisch Null! In den seltensten Fälle steht an dieser Stelle einfach 0. Wir als Anwender müssen daher immer das Resultat vorsichtig interpretieren.
Loesen der Normalgleichungen¶
Da die Matrix \(A^T A\) symmetrisch positiv definit ist, ergibt sich für die Lösung des linearen Ausgleichsproblems folgende Methode:
Berechne \(A^T A\), \(A^T b\).
[24]:
ATA = A.T@A
ATA
[24]:
array([[1.3049395 , 1.89728507],
[1.89728507, 6. ]])
[25]:
ATb = A.T@y
ATb
[25]:
array([1.24481532, 5.05135747])
Berechne die Cholesky-Zerlegung
\[L L^T = A^TA\]von \(A^T A\).
[26]:
from scipy.linalg import cholesky
[27]:
L = cholesky(ATA,lower = True)
L
[27]:
array([[1.14233948, 0. ],
[1.66087673, 1.80041342]])
Löse
\[L z = A^T b,\quad L^T x = z\]durch Vorwärts, bzw. Rückwärtseinsetzen.
[28]:
from scipy.linalg import solve_triangular
[29]:
z = solve_triangular(L,ATb,lower = True)
x = solve_triangular(L.T,z,lower = False)
x
[29]:
array([-0.5, 1. ])
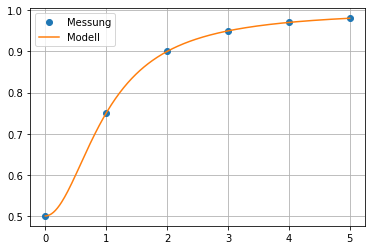
Die Reihenfolge der Koeffizienten korrespondiert mit der Reihenfolge der gewählten Ansatz- / Basisfunktion.
Es folgt
[30]:
tp = np.linspace(0,5,300)
Atp = u(tp)
plt.plot(t,y,'o',label='Messung')
plt.plot(tp, Atp@x,label='Modell')
plt.legend()
plt.grid()
plt.savefig('ExmpLinRegression3.pdf')
plt.show()
