Schrittweitensteuerung bei Einschrittverfahren

Lernziele

Sie implementieren ein explizites Runge-Kutta-Verfahren mit eingebettetem Fehlerschätzer zuerst mit konstanter Schrittweite und dann mit Schrittweitensteuerung. Sie testen Ihre Implementierung an einem Modellproblem.

Theorie

Ein eingebettetes Runge-Kutta-Verfahren (Steigungsform) der Ordnung \(p(\hat{p})\) (\(p \neq \hat{p}\)) ist von der Form

(1)\[\begin{split}\begin{array}{c|cccc} c_1 & a_{11} & a_{12} & \cdots & a_{1s}\\ c_2 & a_{21} & a_{22} & \cdots & a_{2s}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ c_s & a_{s1} & a_{s2} & \cdots & a_{ss}\\ \hline y_{k+1} & b_1 & b_2 & \cdots & b_s\\ \hat{y}_{k+1} & \hat{b}_1 & \hat{b}_2 & \dots & \hat{b}_s \end{array} \quad \begin{array}{rcl} r_1 &=& f(x_{k}+c_1h,y_{k}+h\,(a_{11}r_1+a_{12}r_2+\cdots+a_{1s}r_s))\\ r_2 &=& f(x_{k}+c_2h,y_{k}+h\,(a_{21}r_1+a_{22}r_2+\cdots+a_{2s}r_s))\\ &\vdots&\\ r_s &=& f(x_{k}+c_sh,y_{k}+h\,(a_{s1}r_1+a_{s2}r_2+\cdots+a_{ss}r_s))\\ y_{k+1} &=& y_{k} + h\,(b_1 r_1 + b_2 r_2 + \cdots + b_s r_s)\\ \hat{y}_{k+1} &=& y_{k} + h\,(\hat{b}_1 r_1 + \hat{b}_2 r_2 + \cdots + \hat{b}_s r_s) \end{array}\end{split}\]

wobei in jedem RK-Schritt aus denselben Steigungen \(r_1,r_2,\dots,r_s\) zwei Näherungen \(y_{k+1}\) bzw. \(\hat{y}_{k+1}\) mit Verfahren der Konsistenzordnung \(p\) bzw. \(\hat{p}\) berechnet werden (üblicherweise gilt \(|p-\hat{p}| = 1\)). Anhand des Fehlerschätzers \(T := |y_{k+1}-\hat{y}_{k+1}| \approx \eta\) wird entschieden, ob der Wert \(y_{k+1}\) akzeptiert wird und ob die Schrittweite verändert werden soll. Eine mögliche Strategie dafür ist (mit einer Fehlerschranke \(\mathrm{tol} > 0\)):

(2)\[\begin{split}\begin{array}{rl} T < \frac{\mathrm{tol}}{20}: & y_{k+1} \textrm{ akzeptieren, Schrittweite verdoppeln: } h \leftarrow 2h\\ \frac{\mathrm{tol}}{20} \leq T \leq \mathrm{tol}: & y_{k+1} \textrm{ akzeptieren, Schrittweite unverändert lassen}\\ T > \mathrm{tol}: & y_{k+1} \textrm{ ablehnen, Schrittweite halbieren: } h \leftarrow \frac{h}{2} \end{array}\end{split}\]

Dies tun wir so lange, bis wir bei der Endstelle angekommen sind. Das Ziel der Schrittweitensteuerung ist, die Endstelle mit einer minimalen Anzahl Schritte zu erreichen, wobei die vorgegebene Genauigkeit in jedem Schritt eingehalten wird.

Bemerkungen:

  • Für einen fairen Vergleich mit anderen RK-Verfahren ist zu beachten, dass auch abgelehnte Schritte Rechenzeit kosten! Einige häufig verwendete eingebettete Runge-Kutta-Verfahren sind

    Autor(en)

    Jahr

    Ordnung

    Stufen

    Bemerkung

    Fehlberg

    1969

    4(5)

    6

    zwei unterschiedliche Verfahren,

    die beide mit RKF45 bezeichnet werden

    Dormand,

    Prince

    1980

    5(4)

    7

    DOPRI5, verwendet in MATLABs ode45

    und in scipy.integrate.ode

    Bogacki,

    Shampine

    1989

    3(2)

    4

    verwendet in MATLABs ode43

    Cash-Karp

    1990

    5(4)

    6

    verwendet in LabVIEW

  • Falls die Schrittweite \(h\) akzeptiert wird, dann wird immer die Näherung \(y_{k+1}\) (mit Ordnung \(p\)) übernommen, um die Steigungen im nächsten RK-Schritt zu berechnen. Die Näherung \(\hat{y}_{k+1}\) (mit Ordnung \(\hat{p}\)) wird nur zur Berechnung des Fehlerschätzers verwendet. Daher funktioniert z. B. ein eingebettetes Runge-Kutta-Verfahren der Ordnung \(5(4)\) anders als eines der Ordnung \(4(5)\)!

Aufträge

  1. (Test-Programme mit konstanter Schrittweite) Mit diesem Test wird sichergestellt, dass Sie alle Koeffizienten des Butcher-Tableaus richtig eingeben.

    Schreiben Sie zwei Programme zur Lösung eines AWPs mit den in RKF45 verwendeten Verfahren gemäss den Butcher-Tableaus

    \[\begin{split}\renewcommand{\arraystretch}{1.2} \begin{array}{ll} \textrm{Ordnung 4:} & \textrm{Ordnung 5:}\\ \begin{array}{c|cccccc} 0 & \\ \frac{2}{9} & \frac{2}{9}\\ \frac{1}{3} & \frac{1}{12} & \frac{1}{4}\\ \frac{3}{4} & \frac{69}{128} & -\frac{243}{128} & \frac{135}{64}\\ 1 & -\frac{17}{12} & \frac{27}{4} & -\frac{27}{5} & \frac{16}{15}\\ \frac{5}{6} & \frac{65}{432} & -\frac{5}{16} & \frac{13}{16} & \frac{4}{27} & \frac{5}{144}\\ \hline & \frac{1}{9} & 0 & \frac{9}{20} & \frac{16}{45} & \frac{1}{12} & 0 \end{array} & \begin{array}{c|cccccc} 0 & \\ \frac{2}{9} & \frac{2}{9}\\ \frac{1}{3} & \frac{1}{12} & \frac{1}{4}\\ \frac{3}{4} & \frac{69}{128} & -\frac{243}{128} & \frac{135}{64}\\ 1 & -\frac{17}{12} & \frac{27}{4} & -\frac{27}{5} & \frac{16}{15}\\ \frac{5}{6} & \frac{65}{432} & -\frac{5}{16} & \frac{13}{16} & \frac{4}{27} & \frac{5}{144}\\ \hline & \frac{47}{450} & 0 & \frac{12}{25} & \frac{32}{225} & \frac{1}{30} & \frac{6}{25} \end{array} \end{array}\end{split}\]

    (die sechs Stufen sind bei beiden Verfahren identisch!). Verwenden Sie die Programmstruktur für explizite Runge-Kutta-Verfahren aus dem Praktikum 9, wobei Sie jetzt in jedem RK-Schritt sechs Steigungen berechnen müssen.

  2. Lösen Sie mit Ihren Programmen aus 1. das Anfangswertproblem

    \[y' + \frac{x^2}{y} = 0, \quad y(0) = -4.\]

    Berechnen Sie für \(X=2\) und \(N=2^{j-1}\), \(j \in \{1,2,\dots,12\}\), jeweils die absoluten Fehler an der Endstelle (\(y(2) = -4\sqrt{\frac{2}{3}}\)). Zeichnen Sie die Fehler gegen die Schrittweiten \(h=\frac{2}{N}\) in einer doppelt logarithmischen Darstellung, und überzeugen Sie sich grafisch von den Konvergenzordnungen \(p=4\) bzw. \(p=5\) der beiden Verfahren.

  3. Schreiben Sie ein Programm zur Lösung eines AWPs mit RKF45 mit Schrittweitensteuerung:

    (3)\[\begin{split}\renewcommand{\arraystretch}{1.2} \begin{array}{c|cccccc} 0 & \\ \frac{2}{9} & \frac{2}{9}\\ \frac{1}{3} & \frac{1}{12} & \frac{1}{4}\\ \frac{3}{4} & \frac{69}{128} & -\frac{243}{128} & \frac{135}{64}\\ 1 & -\frac{17}{12} & \frac{27}{4} & -\frac{27}{5} & \frac{16}{15}\\ \frac{5}{6} & \frac{65}{432} & -\frac{5}{16} & \frac{13}{16} & \frac{4}{27} & \frac{5}{144}\\ \hline y_{k+1} & \frac{1}{9} & 0 & \frac{9}{20} & \frac{16}{45} & \frac{1}{12} & 0\\ \hat{y}_{k+1} & \frac{47}{450} & 0 & \frac{12}{25} & \frac{32}{225} & \frac{1}{30} & \frac{6}{25} \end{array}\end{split}\]

    (gleiche Koeffizienten wie in 1.!). Verwenden Sie die Programmstruktur (vgl. Abbildung 3.8 im Skript):

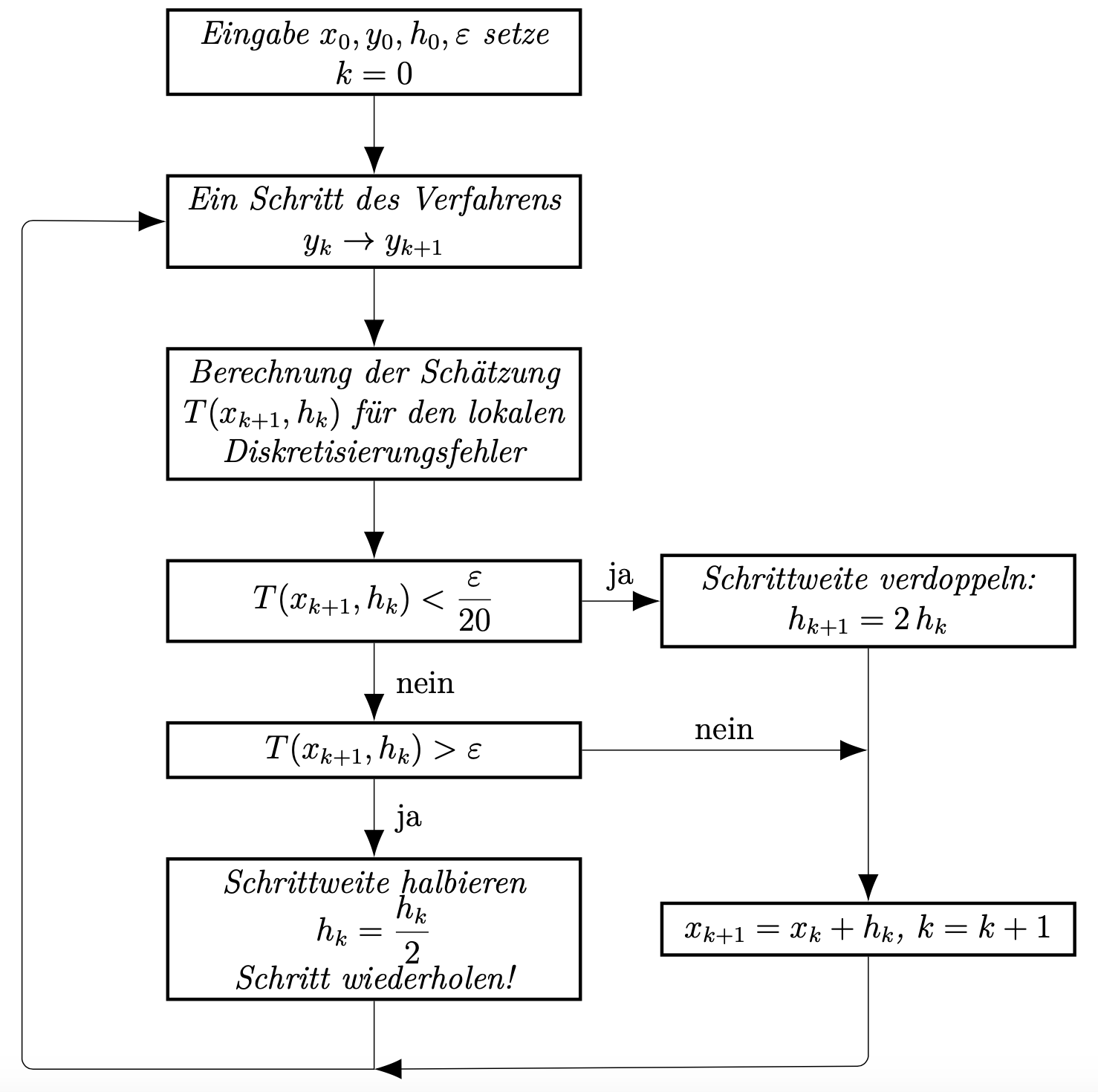
    ../../_images/SchrittweitenSteuerung.png

  4. Testen Sie Ihr Programm aus 3. indem Sie das AWP aus 2. mit RKF45 für \(\mathrm{tol} = 10^{-j}\), \(j \in \{1,2,\dots,12\}\), lösen. Berechnen Sie jeweils den maximalen absoluten Fehler \(\displaystyle \max_k|y_k - y(x_k)|\).

    Hinweis: exakte Lösung \(\displaystyle y(x) = -\sqrt{16-\frac{2}{3}x^3}\), \(x \leq 2 \cdot 3^{1/3}\).

Abgabe

Bitte geben Sie Ihre Lösungen bis spätestens vor dem nächsten Praktikum ab.