Numerische Methoden für Systeme¶
Lernziele¶
Im vorliegenden Praktikum sollen folgende Lernziele erreicht werden:
Sie verstehen die wesentlichen Unterschiede zwischen impliziten und expliziten Verfahren.
Sie können verschiedene explizite und implizite Diskretisierungsverfahren für Anfangswertprobleme implementieren.
Sie können das Netwon-Verfahren zur Lösung eines Systems im Rahmen der Zeitschrittintegration implementieren.
Sie können den Unterschied zwischen konservativen Diskretisierungsverfahren und nicht konservativen Verfahren erklären, sowie das Verhalten dieser Verfahren insbesondere für physikalische Stabilitätsprobleme verstehen.
Theorie¶
Der Numeriktheorieteil ist in der Vorlesung im Kapitel 3.4 (vgl. Skript) dargestellt. In Natur und Technik treten bei viele Vorgänge Stabilitätsprobleme auf. So wird z.B. die Strömung über einen Tragflügel bei Verkehrsflugzeugen ab einem bestimmten Punkt instabil und geht vom laminaren zum turbulenten Zustand über. Dieser Umschlagpunkt kann mit Hilfe von numerischen Simulationen gefunden werden. Oder die Ausbreitung von Viren in der Bevölkerung (z.B. Corona-Viren) folgt einem Exponentialgesetz als Lösung von Differentialgleichungen. Wenn der Exponent grösser als 1 ist, steigt die Anzahl der infizierten Personen exponentiell an, wenn er kleiner als 1 ist nimmt die Zahl exponentiell ab.
Andere Stabilitätsprobleme treten zum Beispiel beim harmonischen Oszillator auf, der sich sehr gut für die prinzipielle Untersuchung von Stabilitätsproblemen eignet. Im vorliegenden Projekt sollen die Bewegungsgleichungen eines harmonischen Oszillators numerisch gelöst werden. Wobei der Reibungsterm gegeben durch den Windwiderstand nichtlinear ist.
Wichtig bei der Modellierung ist, dass das Stabilitätsverhalten vom numerischen Verfahren richtig beschrieben wird.
Verständnisfragen¶
Was verstehen Sie unter einem konservativen numerischen Verfahren?
Das klassische Runge-Kutta-Verfahren ist ”nahezu” konservativ. Was bedeutet das? Worauf müssen Sie achten, wenn Sie das Runge-Kutta-Verfahren für die Lösung von Stabilitätsproblemen einsetzen wollen.
Aufgaben¶
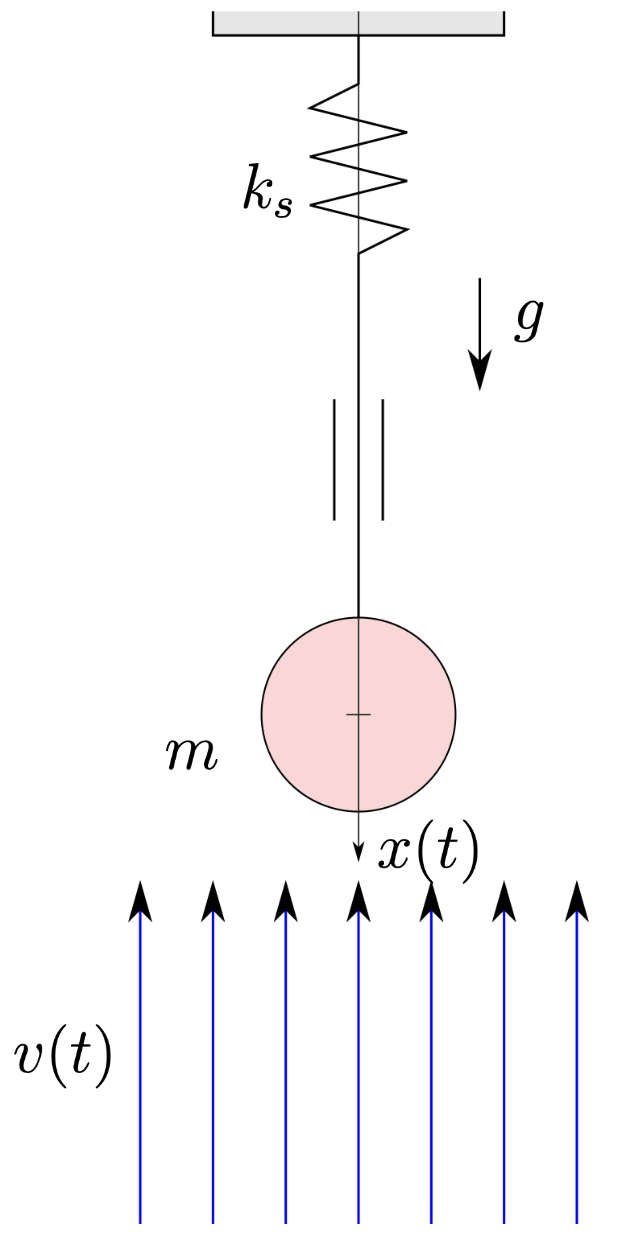
Wir betrachten eine Kugel mit der Masse \(m\), welche an einer Feder aufgehängt und von unten mit Luft angeströmt wird. Die Position der Kugel sei \(x(t)\) und seitlich reibungsfrei geführt. Die Luft hat die Geschwindigkeit \(v(t)\). Diese kann eingestellt werden. Die Auftriebskraft von umströmten Objekten kann wie folgt modelliert werden:
Diese Kraft ist abhängig von der Luftdichte \(\rho\), von dem Auftriebsbeiwert \(C_a\), von der Querschnittsfläche des Objekts \(A\), und von der relativen Anströmgeschwindigkeit \(v_{\text{rel}}\).
Für die Feder wird angenommen, dass sie eine lineare Charakteristik mit der Federsteifigkeit \(k_s`\) hat und masselos ist. Die Ruhelage der Feder ist bei \(x=0\). Die Gleichgewichtsposition der Kugel wird mit \(w_e\) bezeichnet.
Im Weiteren setzen wir voraus, dass die Luftgeschwindigkeit \(v(t) \equiv v_0\) konstant ist und die Parameter wie folgt gegeben sind:
wobei die Federkonstante bewusst sehr klein gewählt ist, um verschiedene Effekte gut zu sehen.
Modellieren Sie mit Hilfe einer Differentialgleichung zweiter Ordnung die Bewegung der Kugel. Berücksichtigen Sie dabei, dass \(F_a\) der Bewegung immer entgegen wirkt. In der Kräftebilanz muss daher \(F_a\) unter Berücksichtigung von \(\text{sign}(v_{\text{rel}})\) einfliessen. Bilden Sie die Kräftebilanz mit
Massenkraft \(F_m = m\,\ddot{x}(t)\)
Nichtlineare Reibungskraft \(F_a = k\, v_{\text{rel}}^2,\ \text{mit}\ v_{\text{rel}}=\dot{x}(t)+v_0\)
Federkraft \(F_k = k_s\, x(t)\)
Gravitationskraft \(F_g = m\, g\).
Die Kugel befindet sich zum Zeitpunkt \(t=0\) ruhend in der neutralen Position der Feder.
Wie lautet das Anfangswertproblem mit Hilfe einer Differentialgleichung 2. Ordnung?
Wie lautet das Anfangswertproblem als System 1. Ordnung?
Implementieren Sie das klassische Runge-Kutta-Verfahren 4. Ordnung für Differentialgleichungssysteme zur Lösung des Anfangswertproblems.
Validieren Sie Ihre Lösung mit Hilfe der folgenden Überlegungen:
Bestimmen Sie sich analytisch, gegen welche Auslenkung \(x(t)\) für \(t\to\infty\) konvergiert? (Gleichgewichtsposition \(w_e\).) Diesen Wert können Sie später für die Validierung Ihrer numerischen Simulation zu hilfe nehmen.
Hinweis: Wenn wir davon aus gehen, dass für \(t\to\infty\) eine stationäre Lösung folgt, so muss in dem Fall \(\lim_{t\to\infty}\dot{x}(t) = 0\) erfüllt sein.
Bemerkung: Im Fall \(v(t)\equiv v_0\) konstant, nennt man die Differentialgleichung auch autonom. Es gilt \(f(t,x) = f(x)\). In der Theorie ebener autonomer Systeme nennt man den Punkt \(w_0 = (x_0,x_1)^T\) so, dass \(f(w_0) = 0\) gilt, einen Gleichgewichtspunkt.
Wie gross muss die konstante Luftgeschwindigkeit sein, damit sich die Kugel nicht bewegt. Testen Sie den Fall.
Berechnen Sie numerisch mit Hilfe des Verfahrens für folgende Geschwindigkeiten
\[v_0 \in \left\{0, 4, \frac{\sqrt{k_s\,m}}{k}, 7, \sqrt{\frac{m\,g}{k}}\right\} \text{[m/s]}\]die Lösungen und stellen Sie diese zusätzlich im Phasendiagramm \((x(t), \dot{x}(t))\) dar. Wählen Sie für die Schrittweite \(h=0.25\). Sie sehen, dass wir unterschiedliche Lösungen von der Charakteristik erhalten.
Mit Hilfe der Eigenwerte \(\lambda_j\) der Jacobimatrix \(\partial_x f(t,x)\), ausgewertet im Gleichgewichtspunkt \(w_0\) können wir diese charakterisieren und eine Aussage bezüglich der Stabilität der Lösung machen:
\[\begin{split}\text{Re}(\lambda_j) \begin{cases} < 0 & \quad\text{für alle $j=1,2$, so nennt man den Gleichgewichtspunkt stabil}\\ = 0 & \quad\text{gilt zu dem geometrische Vielfachheit ist gleich der algebraischen,}\\ & \quad\text{so nennt man den Gleichgewichtspunkt grenz stabil}\\ > 0 & \quad\text{andern falls instabil.}\end{cases}\end{split}\]Die Charakteristik ist gegeben durch
\[\begin{split}\begin{split} \lambda_{1,2} \in \mathbb{C} & \quad\text{stabiler ($\text{Re}(\lambda_{1,2})<0$) / instabiler Strudel}\\ \lambda_1 < 0 < \lambda_2 & \quad\text{Sattelpunkt}\\ \lambda_1 = \lambda_2 \in\mathbb{R} & \quad\text{entarteter Knoten (stabil / instabil)}\\ \lambda_{1,2} \in \mathbb{R} & \quad\text{Knoten (stabil / instabil)}\\ \end{split}\end{split}\]Charakerisieren Sie die verschiedenen Lösungen, in dem Sie die Eigenwerte der Jacobimatrix in den Gleichgewichtspunkte analysieren.
Berechnen Sie die Lösungen aus 3. nun mit der impliziten Mittelpunktregel:
\[\begin{split}\begin{aligned} r_1 &= f(t_k+h/2, x_k + h/2\cdot r_1)\\ x_{k+1} &= x_k + h\,r_1~.\end{aligned}\end{split}\]Hierbei sind \(x_k, x_{k+1}\) Vektoren mit \(x_k=(x(t_k),\dot{x}(t_k))^T\), und \(f\) ist eine vektorwertige Funktion. Da die erste Gleichung nur implizit gegeben ist, muss in jedem Zeitschritt ein Gleichungssystem gelöst werden. Stellen Sie wieder die Lösung zeitabhängig und im Phasendiagramm dar.
Vergleich der beiden Verfahren: Berechnen Sie für \(v_0=0\), \(k=0\) und \(k_s=0.05\) N/m jeweilen mit dem klassische Runge-Kutta-Verfahren 4. Ordnung und der impliziten Mittelpunktregel eine Lösung. Um den Effekt zu verstärken können Sie \(h=0.8\) oder noch etwas grösser benutzen. Vergleichen Sie die beiden Lösungen, in dem Sie die „Energie“
\[E(t) = \frac{1}{2}\, k_s\, \left(x(t)- \frac{m\,g}{k_s}\right)^2 + \frac{1}{2}\, m\, \dot{x}(t)^2\]graphisch darstellen. Betrachten Sie ebenfalls die Lösungen in der Phasenebene, in dem Sie Punkte für die Darstellung benutzen. Welche Lösung ist physikalisch korrekt?
Abgabe¶
Bitte geben Sie Ihre Lösungen bis spätestens vor dem nächsten Praktikum ab.