Einführung partielle Differentialgleichungen¶

Lernziele¶

Im vorliegenden Praktikum sollen folgende Lernziele erreicht werden:

Den Zusammenhang von räumlicher und zeitlicher Diskretisierung verstehen und entsprechende Zeitschritt-Restiktionen bestimmen können.
Das Forward Time Centred Space Schema (FTCS-Schema) für Dirichlet- und Neumann-Randbedingungen implementieren können.
Das implizite Crank-Nicolson-Verfahren zuammen mit dem zentrale Differenzen-Verfahren implementieren können.

Theorie¶

Der Theorieteil ist in der Vorlesung im Kapitel 4.2 (vgl. Skript) dargestellt. Die praktische Implementation von Randbedingungen wird in der Literatur nur selten ausführlich gezeigt. Dies soll im vorliegenden Projekt geübt werden.

Verständnisfragen¶

Was sind die Vor- und Nachteile von expliziten Zeitschrittverfahren gegenüber impliziten Zeitschrittverfahren? Für welche Fälle würden Sie implizite Verfahren vorziehen?
Erklären Sie die Unterschiede zwischen Dirichlet- und Neumann-Randbedingungen und deren Implementierung in einem zentrale Differenzen Schema für die DGL:

\[u''(x)=f(x).\]

Aufgaben¶

Aufgabe 1¶

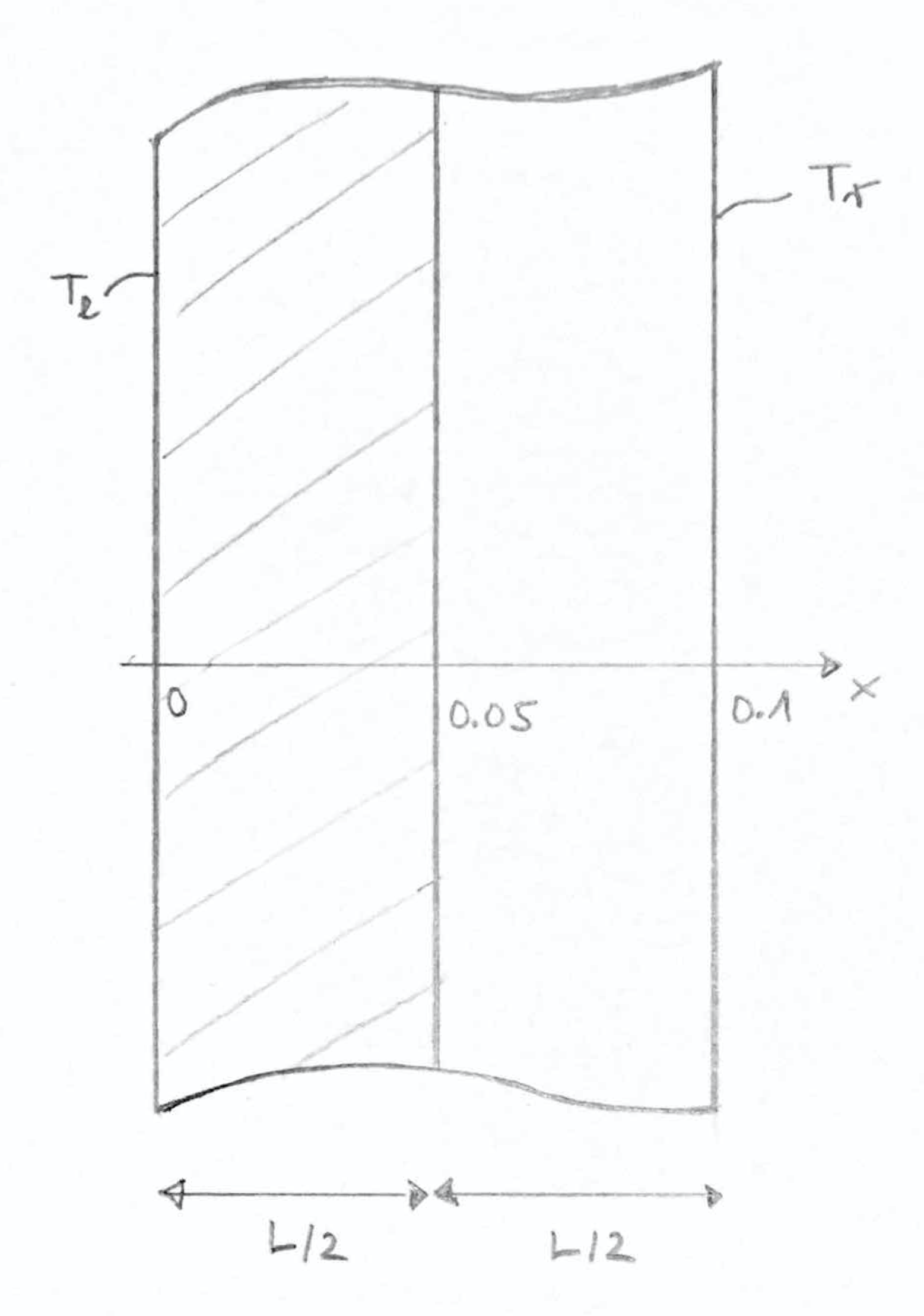
Zwei grosse Platten der Dicke \(L/2\) werden zum Zeitpunkt \(t=0\) in Kontakt gebracht (optimaler Wärmekontakt), Skizze s. u. Die linke Platte hat die Temperatur \(T_l=100^\circ C\) und die rechte Platte die Temperatur \(T_r=0^\circ C\). Die Wärmeleitung wird durch die Wärmeleitungsgleichung beschrieben:

\[\frac{\partial T}{\partial t}-\,\frac{\lambda}{\rho\,c}\,\frac{\partial^2T}{\partial x^2}=0\,,\]

wobei \(\rho\) die Dichte, \(c\) die spezifische Wärmekapazität und \(\lambda\) die Wärmeleitfähigkeit bezeichnen.

Dieses Problem soll für zwei Stahlplatten der Dicke \(L/2=5cm\) mit Matlab numerisch gelöst werden. Wobei hier Cr-Ni-Stahl mit einer Temperaturleitfähigkeit von

\[a = \frac{\lambda}{\rho\,c} = 3.8\cdot 10^{-6} m^2/s\]

angenommen werden soll.

Betrachten Sie den Fall isothermer Randbedingungen, d.h. die Temperaturen \(T_l=100^\circ C\) und \(T_r=0^\circ C\) werden konstant vorgegeben (der linke Rand der Platten wird geheizt und der rechte gekühlt). Diskretisieren Sie die Wärmeleitungsgleichung mit dem Forward Time Centred Space Schema (FTCS-Schema). Beachten Sie, dass für das FTCS-Schema die Zeitschritt-Restriktion

\[s=a \frac{\tau}{h^2} \le \frac{1}{2}\]

gilt. Verwenden Sie in x-Richtung \(J=31\) Stützstellen und wählen Sie \(\tau\) gemäss der obigen Bedingung. Wie lange dauert es, bis sich die Temperatur zwischen zwei Zeitschritten \(T_{n+1}, T_n\) punktweise weniger als \(0.1^\circ C\) ändert? Plotten Sie die erhaltenen Temperaturverläufe.
Betrachten Sie nun den adiabatischen Fall, d.h. für die Ränder gilt:

\[\begin{split}0=\left. \frac{\partial T}{\partial x}\right|_{x=0m} \,, \\ 0=\left. \frac{\partial T}{\partial x}\right|_{x=0.1m} ~.\end{split}\]

Verwenden Sie wiederum das FTCS-Schema und zeigen Sie, dass für die Implementierung der Neumann-Randbedingungen mit zentralen Differenzen an den Randpunkten \(x_1\) und \(x_{J}\) gilt:

\[\begin{split}\begin{aligned} T_{n+1,0} &=2\,a\,\frac{\tau}{h^2}\,(T_{n,1}-T_{n,0})+T_{n,0}\\ T_{n+1,J} &=2\,a\,\frac{\tau}{h^2}\,(T_{n,J-1}-T_{n,J} )+T_{n,J}~. \end{aligned}\end{split}\]

Verwenden Sie in x-Richtung \(J=11\) Stützstellen und wählen Sie \(\tau\) gemäss der obigen Zeitschritt-Restriktion. Nach welcher Zeit ändert sich das Temperaturfeld für diesen Fall punktweise um weniger als \(0.1^\circ C\)? Plotten Sie die erhaltenen Temperaturverläufe.

Aufgabe 2¶

Um die Zeitschritt-Restriktion zu umgehen, bietet sich die Verwendung eines impliziten Verfahrens an. Benutzen Sie das Crank-Nicolson-Verfahren für die Zeitintergration und das zentrale Differenzenverfahren für die räumliche Integration. Da das Crank-Nicolson-Verfahren implizit ist, muss in jedem Zeitschritt ein lineares Gleichungssystem gelöst werden. Die Diskretisierung führt auf ein System der Form

\[A\,u_{n+1}=b_{n+1},\]

mit einer konstanten Tridiagonal-Matrix \(A\) und dem zeitabhängigen Vektor \(b_{n+1}\). Leiten Sie die Matrix und den Vektor her.

Wir betrachten nun den Fall aus 1.1 mit denselben Koeffzienten \(a\) und Dirichlet-Randbedingungen \((T_l=100^\circ C,~T_r=0^\circ C)\). Berücksichtigen Sie die Dirichlet-Randbedingungen indem Sie die Matrix \(A\) geeignet modifizieren. Die Matrix \(A\) ist dann invertierbar. Berechnen Sie die LR-Zerlegung von \(A\) und lösen Sie das System nur noch durch Vorwärts- und Rückwärtseinsetzen in jedem Zeitschritt oder verwenden Sie alternativ den Thomas-Algorithmus (Algorithmus 2.6 im Skript).

Bestimmen Sie den Zeitpunkt, ab dem sich die Lösung \(T_{n+1}\) (punktweise) weniger als \({10^{-5}}^\circ C\) ändert (also wir fordern hier ein deutlich höhere Genauigkeit als mit dem FTCS-Verfahren). Plotten Sie die erhaltenen Temperaturverläufe.
(optional) Schätzen Sie die Anzahl der Zeitschritte ab, die Sie mit dem FTCS-Schema benötigen würden, um dieselbe Genauigkeit zu erreichen (Vergleich der Anzahl Zeitschritte angeben). Vergleichen Sie auch den Rechenaufwand pro Zeitschritt der beiden Verfahren (FTCS, Crank-Nicolson).

Hinweis: Sie können einen deutlich grösseren Zeitschritt als in 1.1 verwenden.

Abgabe¶

Bitte geben Sie Ihre Lösungen bis spätestens vor dem nächsten Praktikum ab.