Kapazität des Plattenkondensators

import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import solve_triangular

Lernziele

Im vorliegenden Praktikum sollen folgende Lernziele erreicht werden:

• Sie verstehen den Unterschied einer gewöhnlichen und partiellen Differentialgleichung.

• Sie kennen die Laplace-Gleichung und verstehen ihre Anwendung in der Elektrostatik.

• Sie verstehen die Methode der finiten Differenzen und können sie im zweidimensionalen Raum anwenden.

• Sie kennen die Dirichlet-Randbedingung.

Aufgaben

Die Umsetzung der Aufgaben ist nicht ganz einfach und kann sehr zeitaufwändig werden. Daher wird das Praktikum stark geführt. Es gibt viele Punkte die selbständig umgesetzt werden sollen. Diese sind mit

<snipp selber machen>

gekennezeichnet.

1. Lesen Sie sich in die physikalischen Grundlagen ein. Die Elektrostatik führt uns zur „einfachsten“ partiellen Differentialgleichung.

2. Verstehen Sie die Idee der Finiten Differenzen für den Laplace Operator in der Ebene.

3. Verstehen Sie das Randwertproblem

4. Lösen Sie das Gleichungssystem mit Hilfe der implementierten Cholesky-Zerlegung und Vorwärts- / Rückwärtseinsetzen.

5. Berechnen und vergleichen Sie die Kapazität

6. Erweitern Sie den Code für das Problem mit einem Dielektrikum mit \(\varepsilon = 21\).

Physikalische Grundlagen

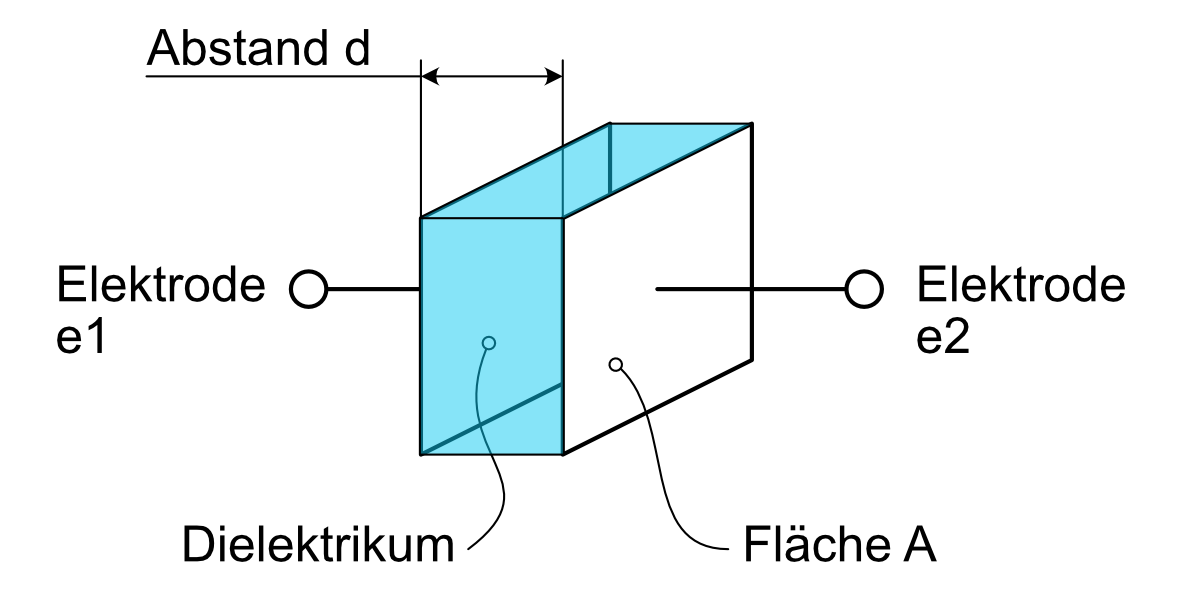
Im Praktikum berechnen wir das elektrische Feld \(\vec{E}\) eines Plattenkondensators und die dazu gehörige Kapazität \(C\). Die berechnete Kapazität können wir mit der bekannten Näherungsformel für den Plattenkondensator vergleichen. Es gilt

\[C \approx \varepsilon_0\,\varepsilon_r \frac{A}{d},\]

wobei \(A\) die Fläche und \(d\) die Distanz zwischen den Platten bzw. Elektroden bezeichnet. Die relative elektrische Permittivität \(\varepsilon_r\) ist eine Materialkonstante, welche die Polarisationsfähigkeit relativ zum Vakum quantifiziert.

eps0 = 8.8541878188e-12
def CPlatte(epsr, A, d):
    return eps0*epsr*A/d

Die Maxwell Gleichung (Faraday’s Gesetz)

\[\nabla\times \vec{E}(t,\vec{x}) = \partial_t \vec{B}(t,\vec{x})\]

beschreibt die Wechselwirkung zwischen dem elektrischen und magnetischen Feld. Für statische Felder (dh. zeitunabhängige) gilt \(\partial_t \vec{B}(t,\vec{x})=0\). Aus dem Gesetz von Faraday folgt somit

\[\nabla\times \vec{E}(t,\vec{x})=0,\]

dass das elektrische Feld wirbelfrei ist. In dem Fall kann \(\vec{E}(\vec{x})\) durch ein Gradienten-Feld beschrieben werden (vgl. AN3). Daher führen wir das elektrische Potential \(\varphi: \Omega \to \mathbb{R}\) ein und definieren

\[\vec{E}(\vec{x}) = -\nabla \varphi(\vec{x}).\]

Mit Hilfe der Ladungserhaltung, dem Gauss’schen Gesetz folgt

\[\operatorname{div}(\epsilon \vec{E}(\vec{x})) = q(\vec{x}).\]

Für die Annahme, dass keine Ladungsverteilung gegeben ist, daher \(q(\vec{x}) \equiv 0\) für alle \(\vec{x}\in\Omega\) gilt, folgt für das elektrische Potential die Laplace-Gleichung

\[-\operatorname{div}(\epsilon \nabla\varphi(\vec{x})) = 0\quad \text{für}\ \vec{x}\in\Omega.\]

Mathematisches Problem

Die Laplace Gleichung ist eine partielle Differential Gleichung anwendungsbedingt im \(\mathbb{R}^3\). Im Praktikum betrachten wir das Problem jedoch im \(\Omega \subset \mathbb{R}^3\). Die Abbildung unten zeigt das Gebiet \(\Omega \subset \mathbb{R}^2\) in der Ebene. Wir nehmen daher als Vereinfachung ins zweidimensionale an, dass die Linie für den Kondensator in die Tiefe gezogen werden kann und vernachlässigen die Randeffekte in diese Richtung.

Da wir mit einer überschaubaren Anzahl Freiheitsgrade, bzw. Unbekannte rechnen wollen, müssen wir das Gebiet beschränken und Annahmen bezüglich Randwerte treffen:

• Auf dem äusseren Rand gehen wir von Dirichlet-Randwerte aus, das bedeutet \(\varphi(\vec{x}) = 0\) [V] für alle \(\vec{x} \in \partial\Omega\).

• Auf der Elektrode e1 sei \(\varphi(\vec{x}) = 1\) [V]

• und auf der Elektrode e2 sei \(\varphi(\vec{x}) = -1\) [V]

• Die Kabel zu den Elektroden werden vernachlässigt (spannen keine Fläche auf).

Damit folgt das zu lösende Randwertproblem

\[\begin{split}\begin{split} -\operatorname{div}(\epsilon \nabla\varphi(\vec{x})) &= 0\quad \text{für}\ \vec{x}\in\Omega.\\ \varphi(\vec{x}) & = 1\quad \text{für}\ \vec{x}\in\Gamma_\text{e1}\\ \varphi(\vec{x}) & = -1\quad \text{für}\ \vec{x}\in\Gamma_\text{e2}\\ \varphi(\vec{x}) & = 0\quad \text{für}\ \vec{x}\in\partial\Omega \end{split}\end{split}\]

h=0.01

n_el = 10# Anzahl Intervalle (Punkte - 1) auf Elektrode
n_d = 5# Anzahl Intervalle zwischen Elektrode

b_el = n_el*h # Breite Elektrode
d_di = n_d*h # Abstand Elektroden

nx_air = 10# Anzahl Intervalle zum Rand horizontal
ny_air = 10# Anzahl Intervalle zum Rand vertikal

b_air = nx_air*h # Abstand Elektrode zum Rand horizontal
h_air = ny_air*h # Abstand Elektrode zum Rand vertikal

(Breite Elektrode, Höhe Dielektrikum, Breite Gebiet)

print('b_el=',b_el, 'd_di=',d_di, 'b_Gebiet=',2*(b_air+b_el/2))

Finite Differenzen Lösung

Um die Lösung numerisch berechnen zu können, müssen wir die Differentialgleichung diskretisieren. Dazu wenden wir den Differenzen-Quotienten in \(x\) und \(y\) Richtung für den Laplace Operator an:

\[\begin{split}\begin{split}\Delta \varphi(x,y) & = \varphi_{xx}(x,y) + \varphi_{yy}(x,y) \\ & \approx \frac{\varphi(x-h,y)-2 \varphi(x,y) + \varphi(x+h,y)}{h^2} + \frac{\varphi(x,y-h)-2 \varphi(x,y) + \varphi(x,y+h)}{h^2}.\end{split}\end{split}\]

Damit folgt für die inneren Punkte eines Gebietes

\[\Delta \varphi(x,y) \approx \Delta_h \varphi(x,y) = \frac{\varphi(x-h,y)+\varphi(x,y-h)-4 \varphi(x,y) + \varphi(x+h,y)+\varphi(x,y+h)}{h^2}.\]

Für Randpunkte kann (und muss auch nicht) die Differenz nicht berechnet werden: so ist zum Beispiel am linken Rand eines Rechteck Gebiets \((x-h,y)\not\in D\). An den Randpunkte und auf den Elektroden ist der Funktionswert des elektrischen Potentials \(\varphi\) gegeben.

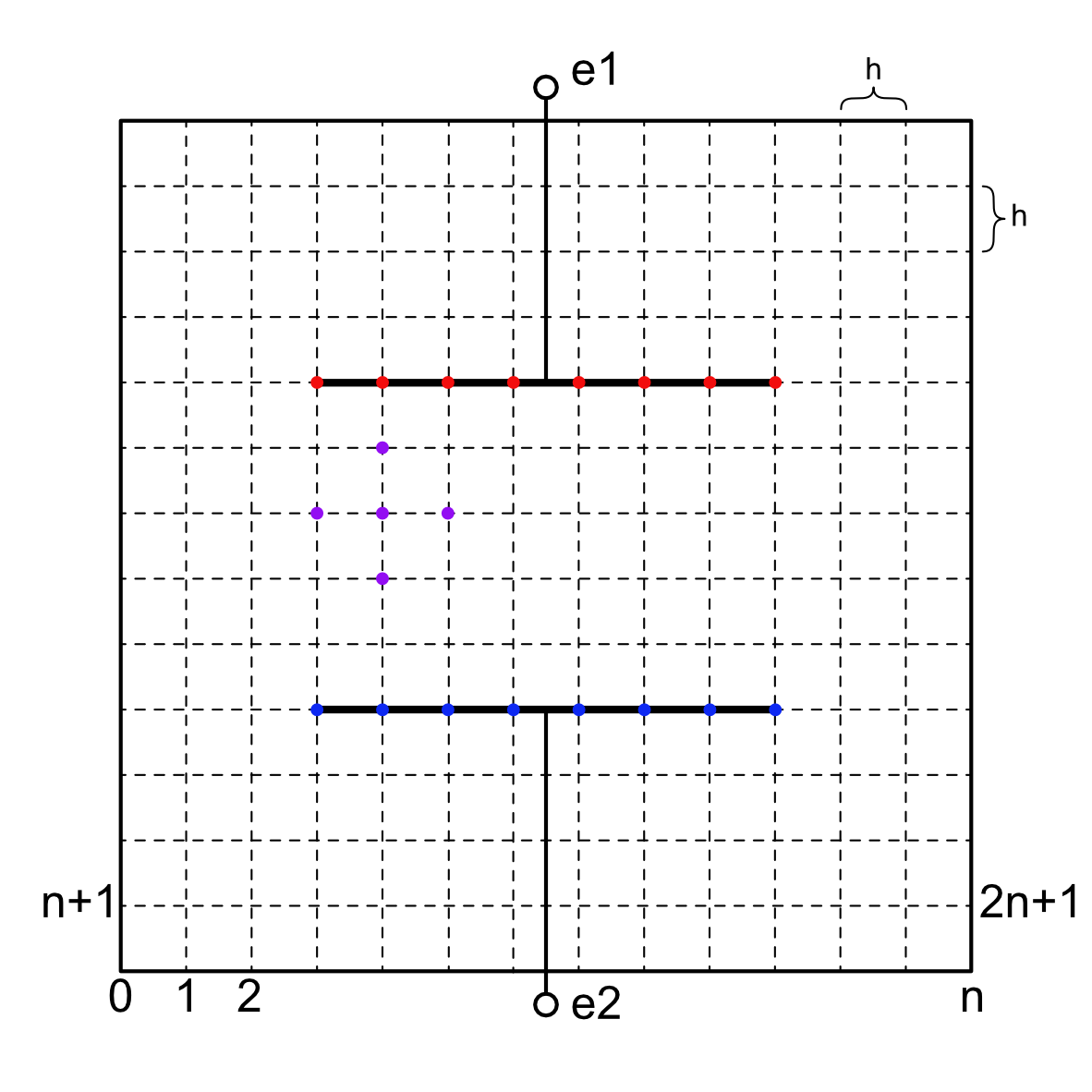
Um die Diskretisierung einfach zu halten, betrachten wir ein quadratisches Gebiet \(\Omega = [-b_{Gebiet}/2,b_{Gebiet}/2]\times[-h_{Gebiet}/2,h_{Gebiet}/2]\subset\mathbb{R}^2\). Sei

\[\varphi_{i,j} = \varphi(x_i, y_j),\]

wobei mit

\[x_i = \frac{i}{n_x},\quad y_j = \frac{j}{n_y}\quad \text{für}\ i = 0,\ldots, n_{x},\ j = 0,\ldots, n_{y}.\]

nx = 2*nx_air+n_el+1
ny = 2*ny_air+n_d+1
xi = np.linspace(-b_air-b_el/2,b_air+b_el/2,nx) # Zerlegung in x-Richtung
yi = np.linspace(-h_air-d_di/2,h_air+d_di/2,ny) # Zerlegung in y-Richtung
Xi,Yi = np.meshgrid(xi,yi) # Berechnet alle Kombinationen in x/y-Richtung
domshape = Xi.shape

Kontrolle, dass die Zerlegung die gewünschte Schrittweite identisch in beide Richtungen \(x,y\) hat:

xi[1]-xi[0], yi[1]-yi[0]

Sämtliche diskrete Punkte im Gebiet sind gegeben durch:

pnts = np.array([Xi.flatten(),Yi.flatten()]).T

Wir müssen nun die freien Freiheitsgrade, daher Punkte für die wir die Lösung des Potentials berechnen müssen und die Punkte mit gegebenen Werten (Dirichlet Freiheitsgrade) bestimmen.

ndofs = pnts.shape[0]
dofs = np.arange(0,ndofs)
inde1 = (-b_el/2-h/2<=pnts[:,0])*(pnts[:,0]<=b_el/2+h/2)*(-d_di/2-h/2<pnts[:,1])*(pnts[:,1]<=-d_di/2+h/2)
inde2 = (-b_el/2-h/2<=pnts[:,0])*(pnts[:,0]<=b_el/2+h/2)*(d_di/2-h/2<pnts[:,1])*(pnts[:,1]<=d_di/2+h/2)
indBND = (pnts[:,0]<xi[0]+h/2)+(xi[-1]-h/2<pnts[:,0])+(pnts[:,1]<yi[0]+h/2)+(yi[-1]-h/2<pnts[:,1])
freedofs = dofs[(~indBND)*(~inde1)*(~inde2)]

plt.plot(pnts[:,0],pnts[:,1],'.')
plt.plot(pnts[freedofs,0],pnts[freedofs,1],'x',alpha=0.75)
plt.plot(pnts[inde1,0],pnts[inde1,1],'o')
plt.plot(pnts[inde2,0],pnts[inde2,1],'o')
plt.plot(pnts[indBND,0],pnts[indBND,1],'o',alpha=0.75)
plt.gca().set_aspect(1)
plt.title('Diskretisiertes Rechengebiet')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

Für das elektrische Potential setzen wir aufgrund der Dirichlet Randwerte

\[\varphi(\vec{x}) = \varphi_i(\vec{x}) + \varphi_0(\vec{x}),\]

wobei mit \(\varphi_0(\vec{x})\) die Dirichlet Randwerte bezeichnen. Da wir \(\varphi_i(\vec{x})\) berechnen, kann \(\varphi_0(\vec{x})\) im Innern beliebige Werte annehmen, wir sezten diese einfach auf Null. Es gilt daher

phi0 = np.zeros_like(dofs,dtype=float)
phi0[inde1]=-1
phi0[inde2]=+1

Für alle inneren Punkte,bzw. freien Freiheitsgrade haben wir das Gleichungssystem

\[\frac{-\varphi_{i-n}-\varphi_{i-1}+4\, \varphi_{i}-\varphi_{i+1}-\varphi_{i+n}}{h^2} =0 \quad i \in \text{freedofs},\]

wobei \(\varepsilon\not=0\) in dem Fall gekürzt wurde. Das können wir im zweiten Teil nicht machen. Da das Gleichungssystem linear ist, können wir dieses in der Form

\[A\cdot\vec{\varphi} = 0\]

als ein grosses System schreiben. Die Berechnung der Matrix \(A\) erfolgt mit Hilfe des „Stencils“, dem relativen Index und dem Gewicht für diese.

stencil = np.array([4,-1,-1,-1,-1])    #
indstencil = np.array([0,-1,1,-nx,nx]) # relativer Index fuer den Differenzen-Quotient

plt.figure(figsize=(10,10))
plt.plot(pnts[:,0],pnts[:,1],'.')
plt.plot(pnts[inde1,0],pnts[inde1,1],'o')
plt.plot(pnts[inde2,0],pnts[inde2,1],'o')
plt.plot(pnts[freedofs,0],pnts[freedofs,1],'x',alpha=0.75)

# Visualisierung des Stencils
plt.plot(pnts[511+indstencil,0],pnts[511+indstencil,1],'o',color='red',alpha=0.75)
plt.gca().set_aspect(1)
plt.show()

Der Lösungsvektor \(\vec{\varphi}\) beinhaltet alle Freiheitsgrade, daher gilt \(\vec{\varphi}\in\mathbb{R}^{\text{ndofs}}\). Mit \(A\in\mathbb{R}^{\text{ndofs}\times\text{ndofs}}\ \) können wir für alle freien Freiheitsgrade die Matrix Einträge berechnen. Dabei werden auch Dirichlet Freiheitsgrade benutzt: im Plot oben sieht man, dass für den Index 511 (daher Zeile 511) ein Wert der Elektrode e1 ins Gleichungssystem eingeht (Spalte). Für Zeilen mit Dirichlet Randwerte gibt es in der Matrix \(A\) keine Einträge. Wir könnten daher die Anzahl Zeilen der Matrix \(A\) auf die Anzahl freien Freiheitsgrade beschränken, lassen das aber der Einfachheit halber sein.

A=np.zeros((ndofs,ndofs))
for i in range(len(freedofs)): # Daher über alle Zeilen
    A[freedofs[i],freedofs[i]+indstencil] = <snipp selber machen> # Stencil wird nur bei den inneren Freiheitsgrade dazu addiert.

Die Matrix für die freien Freiheitsgrade können wir aus \(A\) nehmen:

plt.spy(A[np.ix_(freedofs,freedofs)])

Mit dem Ansatz \(\varphi(\vec{x}) = \varphi_i(\vec{x}) + \varphi_0(\vec{x}),\) folgt

\[A \cdot \vec{\varphi} = A \cdot (\vec{\varphi}_i + \vec{\varphi}_0) = 0\]

Für die inneren, unbekannten Freiheitsgrade \(\vec{\varphi}_i\) folgt somit die Gleichung

\[A \cdot \vec{\varphi}_i = - A \cdot \vec{\varphi}_0.\]

Das Gleichungssystem müssen wir nur für die freien Freiheitsgrade lösen. Daher mit der Matrix

\[A_{\text{red}} = (A_{i,j},\quad i,j \in \text{freedofs})\]

und der rechten Seite

\[\vec{b}_{\text{red}} = ((- A \cdot \vec{\varphi}_0)_i,\quad i \in \text{freedofs})\]

redA = <snipp selber machen>
redb = <snipp selber machen>

Das System ist symmetrisch:

np.sum(np.abs(redA.T-redA))

Wir lösen das (symmetrisch positiv definite) System mit Hilfe der Cholesky-Zerlegung. mychol berechnet \(A = L\cdot D\cdot L^T\) im Gegensatz zu np.linalg.cholesky. Vergleiche dazu den Input Bemerkungen zur Cholesky Zerlegung.

d,L = mychol(redA)
v = <snipp selber machen> # Vorwärtseinsetzen
phired = <snipp selber machen> # Rückwärtseinsetzen

Die Lösung ist somit gegeben durch

• \(\vec{\varphi} = \vec{\varphi}_0\)

• \(\vec{\varphi}_{[\text{freedofs}]} += \vec{\varphi}_{\text{red}}\)

phi = np.array(phi0) # initialisieren mit phi0
phi[freedofs] += <snipp selber machen>
Phi = np.reshape(phi,domshape) # Lösung in Matrix Form für die Visualisierung

Das elektrische Feld berechnen wir mit Hilfe des zentralen Differenzen-Quotienten

\[\begin{split}\begin{split} E_x(x_i,y_j) & = (E_{x})_{i,j} \approx \frac{\varphi(x_i+h,y_j)-\varphi(x_i-h,y_j)}{2h}\\ E_y(x_i,y_j) & = (E_{y})_{i,j} \approx \frac{\varphi(x_i,y_j+h)-\varphi(x_i,y_j-h)}{2h} \end{split}\end{split}\]

Ex = np.zeros_like(Phi)
Ey = np.zeros_like(Phi)
Ex[:,1:-1] = <snipp selber machen>
Ey[1:-1,:] = <snipp selber machen>

Damit folgt die Lösung visualisiert

plt.figure(figsize=(8,8))
plt.contourf(Xi,Yi,Phi,np.linspace(-1,1,18),cmap='jet')
plt.plot(pnts[inde1,0],pnts[inde1,1],lw=3)#,color='black')
plt.plot(pnts[inde2,0],pnts[inde2,1],lw=3)#,color='black')
plt.quiver(Xi,Yi,Ex,Ey,angles='xy',scale=1.5e3,color='white',pivot='middle')
plt.gca().set_aspect(1)
plt.xlim(-.1,.1)
plt.ylim(-.05,.05)
#plt.savefig('Plattenkondensator.pdf')
plt.show()

Die Kapazität \(C\) kann mit Hilfe der elektrischen Energie berechnet werden. Es gilt

\[C = \frac{2}{U^2} W_e\]

mit

\[W_e = \frac{1}{2} \int_\Omega \varepsilon |\vec{E}|^2 d\Omega.\]

Die Integration setzen wir auf die einfachst mögliche Art um. Wir summieren einfach die Werte multipliziert mit dem Flächenelement \(h^2\). Die Frage stellt sich über welchen Teil man integriert. Der primäre Unterschied zur Näherungsformel ist hier gegeben.

• Berechnen Sie die Summe über das ganze Gebiet

• Berechnen Sie nur die Summe über das Dielektrikum und Elektroden

Vergleichen Sie die beiden Werte mit der Näherungsformel.

We = 1/2*np.sum(<snipp selber machen>)*h**2
indCond = (-b_el/2-h/2<=pnts[:,0])*(pnts[:,0]<=b_el/2+h/2)*(-d_di/2<pnts[:,1])*(pnts[:,1]<=d_di/2)
We2 = 1/2*np.sum(<snipp selber machen>)*h**2

C_FDM = <snipp selber machen>
C2_FDM = <snipp selber machen>
C_ana = CPlatte(1,b_el*1,d_di)

Abweichung zur analytischen Formel:

C_FDM/C_ana-1, C2_FDM/C_ana-1

Visualisierung des elektrischen Potentials

plt.plot(xi,Phi[domshape[0]//2,:])
plt.title('y = '+str(yi[domshape[0]//2]))

plt.plot(yi,Phi[:,domshape[1]//2],)
plt.title('x = '+str(xi[domshape[1]//2]))

(optional) Mit Dielektrikum

Wir nehmen nun an, dass zwischen den Platten ein Dielektrikum mit einem \(\varepsilon_r = 21\) vorhanden ist. Für die Differenzengleichung folgt damit

\[\varepsilon_r(\vec{x}_i) \frac{-\varphi_{i-n}-\varphi_{i-1}+4\, \varphi_{i}-\varphi_{i+1}-\varphi_{i+n}}{h^2} =0 \quad i \in \text{freedofs ohne Rand Luft-Dielektrikum}\]

Beim Übergang von zwischen verschiedenen Materialparameter müssen wir vorsichtig sein. Hier muss die elektrische Flussdichte \(\vec{D} = \varepsilon \vec{E}\) korrekt ausgewertet werden. Entsprechend haben wir

• linker Rand Luft-Dielektrikum:

  \[-\varepsilon_d \frac{\varphi_{i+1} - \varphi_{i}}{h^2}+ \varepsilon_a \frac{\varphi_{i} - \varphi_{i-1}}{h^2} + \varepsilon_d\frac{-\varphi_{i-n}+2\, \varphi_{i}-\varphi_{i+n}}{h^2} = \frac{-\varepsilon_d\varphi_{i-n}-\varepsilon_a\varphi_{i-1}+(\varepsilon_a+3\varepsilon_d) \varphi_{i} -\varepsilon_d \varphi_{i+1} -\varepsilon_d\varphi_{i+n}}{h^2}\]

• rechter Rand Luft-Dielektrikum:

  \[-\varepsilon_a \frac{\varphi_{i+1} - \varphi_{i}}{h^2}+ \varepsilon_d \frac{\varphi_{i} - \varphi_{i-1}}{h^2} + \varepsilon_d\frac{-\varphi_{i-n}+2\, \varphi_{i}-\varphi_{i+n}}{h^2} = \frac{-\varepsilon_d\varphi_{i-n}-\varepsilon_d\varphi_{i-1}+(\varepsilon_a+3\varepsilon_d) \varphi_{i} -\varepsilon_a \varphi_{i+1} -\varepsilon_d\varphi_{i+n}}{h^2}\]

epsr = 21

Wir separieren die Freiheitsgrade für die Luft und das Dielektrikum:

inddeint = (-b_el/2+h/2<=pnts[:,0])*(pnts[:,0]<=b_el/2-h/2)*(-d_di/2+h/2<pnts[:,1])*(pnts[:,1]<=d_di/2-h/2)
inddeBNDL = (-b_el/2-h/2<=pnts[:,0])*(pnts[:,0]<=-b_el/2+h/2)*(-d_di/2+h/2<pnts[:,1])*(pnts[:,1]<=d_di/2-h/2)
inddeBNDR = (b_el/2-h/2<=pnts[:,0])*(pnts[:,0]<=b_el/2+h/2)*(-d_di/2+h/2<pnts[:,1])*(pnts[:,1]<=d_di/2-h/2)
freedofs_air = dofs[(~indBND)*(~inde1)*(~inde2)*(~inddeint)*(~inddeBNDL)*(~inddeBNDR)]
freedofs_diint = dofs[inddeint]
freedofs_diBNDL = dofs[inddeBNDL]
freedofs_diBNDR = dofs[inddeBNDR]

plt.figure(figsize=(10,10))
plt.plot(pnts[indBND,0],pnts[indBND,1],'.')
plt.plot(pnts[inde1,0],pnts[inde1,1],'o')
plt.plot(pnts[inde2,0],pnts[inde2,1],'o')
plt.plot(pnts[freedofs_air,0],pnts[freedofs_air,1],'o',alpha=0.75)
plt.plot(pnts[freedofs_diint,0],pnts[freedofs_diint,1],'o',alpha=0.75)
plt.plot(pnts[freedofs_diBNDL,0],pnts[freedofs_diBNDL,1],'b^',alpha=0.75)
plt.plot(pnts[freedofs_diBNDR,0],pnts[freedofs_diBNDR,1],'b^',alpha=0.75)

# Visualisierung des Stencils
plt.plot(pnts[413+indstencil,0],pnts[413+indstencil,1],'.',color='white',alpha=1)
plt.gca().set_aspect(1)
plt.show()

Damit können wir wieder die Systemmatrix abhängig vom Gebiet berechnen. Für die Koordinaten im Dielektrikum benutzen wir \(\varepsilon_r \not=1\):

A=np.zeros((ndofs,ndofs))
for i in range(len(freedofs_air)): # Daher über alle Zeilen
    A[freedofs_air[i],freedofs_air[i]+indstencil] = <snipp selber machen> # Stencil wird nur bei den inneren Freiheitsgrade dazu addiert.
for i in range(len(freedofs_diint)): # Daher über alle Zeilen
    A[freedofs_diint[i],freedofs_diint[i]+indstencil] = <snipp selber machen> # Stencil wird nur bei den inneren Freiheitsgrade dazu addiert.
for i in range(len(freedofs_diBNDL)): # Daher über alle Zeilen
    A[freedofs_diBNDL[i],freedofs_diBNDL[i]+indstencil] = <snipp selber machen> # Stencil wird nur bei den inneren Freiheitsgrade dazu addiert.
for i in range(len(freedofs_diBNDR)): # Daher über alle Zeilen
    A[freedofs_diBNDR[i],freedofs_diBNDR[i]+indstencil] = <snipp selber machen> # Stencil wird nur bei den inneren Freiheitsgrade dazu addiert.
redA = A[np.ix_(freedofs,freedofs)]
redb = -(A@phi0)[freedofs]

Das Problem ist symmetrisch:

np.sum(np.abs(redA.T-redA))

d,L = mychol(redA)
v = <snipp selber machen> # Vorwärtseinsetzen
phired = <snipp selber machen> # Rückwärtseinsetzen

phi = np.array(phi0) # initialisieren mit phi0
phi[freedofs] += phired
PhiB = np.reshape(phi,domshape)

ExB = np.zeros_like(PhiB)
EyB = np.zeros_like(PhiB)
ExB[:,1:-1] = <snipp selber machen>
EyB[1:-1,:] = <snipp selber machen>

Damit folgt die Lösung visualisiert

plt.figure(figsize=(8,8))
plt.contourf(Xi,Yi,PhiB,np.linspace(-1,1,18),cmap='jet')
plt.plot(pnts[inde1,0],pnts[inde1,1],lw=3)#,color='black')
plt.plot(pnts[inde2,0],pnts[inde2,1],lw=3)#,color='black')
plt.quiver(Xi,Yi,ExB,EyB,angles='xy',scale=1.5e3,color='white',pivot='middle')
plt.gca().set_aspect(1)
plt.xlim(-.1,.1)
plt.ylim(-.05,.05)
#plt.savefig('ElektrischesFeldPlattenkondensator.pdf')
plt.show()

Berechnen Sie wiederum mit Hilfe der elektrischen Energie die Kapazitäten und vergleichen Sie diese mit der Näherungsformel.

WeB = <snipp selber machen>
We2B = <snipp selber machen>
CB_FDM = <snipp selber machen>
C2B_FDM = <snipp selber machen>
CB_ana = CPlatte(eps0*epsr,b_el*1,d_di)

Abweichung zur analytischen Formel:

CB_FDM/CB_ana-1, C2B_FDM/CB_ana-1

Visualisierung des elektrischen Potentials

plt.plot(xi,Phi[domshape[0]//2,:])
plt.plot(xi,PhiB[domshape[0]//2,:])
plt.title('y = '+str(yi[domshape[0]//2]))
plt.show()

plt.plot(yi,Phi[:,domshape[1]//2],)
plt.plot(yi,PhiB[:,domshape[1]//2],)
plt.title('x = '+str(xi[domshape[1]//2]))
plt.show()