Lineare Ausgleichsrechnung¶

Lernziele¶

Sie erkennen, ob es sich bei einem gegebenem funktionalen Zusammenhang zu einer Reihe von Messungen um ein lineares Ausgleichsproblem handelt.
Sie können die zum Ausgleichsproblem gehörende Normalgleichung formulieren.
Sie kennen den Zusammenhang zwischen Normalgleichung und Minimierung der Fehlerquadratsumme.
Sie können die Kleinste-Quadrate-Lösung durch Cholesky-Zerlegung von \(A^TA\) und Vorwärts- sowie Rückwärtssubstitution berechnen.

Theorie¶

Das Praktikum fokusiert die lineare Ausgleichsrechnung, insbesondere auf die Abschnitte 2.2.1 bis 2.2.3 ohne \(QR\)-Zerlegung und Householder-Transformation.

Aufträge¶

Auftrag 1¶

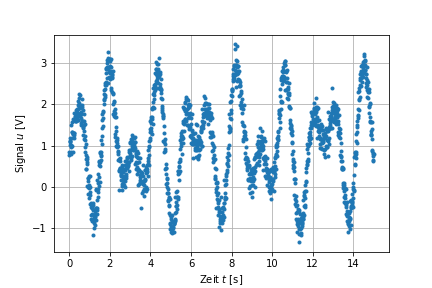
Wir betrachten das Beispiel 2.10 im Skript. Gegeben sei ein periodischer Vorgang zum Beispiel aus einer Messung \((t_i, u_i)\),

für dessen Modellierung durch eine stetige Funktion \(f(t)\) mit gegebener Periode \(T\) eine Linearkombination der trigonometrischen Funktionen

\[\begin{split}\cos(\omega\, k\,t),& \quad k = 0, \ldots, n\\ \sin(\omega\, k\,t),& \quad k = 1, \ldots, n\\ \omega & = \frac{2 \pi}{T}\end{split}\]

verwendet wird. Gesucht sind daher die Koeffizienten \(a_k\) und \(b_k\) von

\[f_n(t) = \frac{1}{2} a_0 + \sum_{k=1}^n \left(a_k \cos(\omega\, k\, t) + b_k \sin(\omega\, k\, t)\right).\]

Aufgaben:

Laden Sie die gegebenen Messdaten aus dem File ‚data.txt‘
```
data = np.genfromtxt('data.txt')
```
In matlab
```
data = readmatrix('data.txt')
```
Visualisieren Sie die Messung. Wie gross ist die Abtastrate? Wie gross schätzen Sie die Grundfrequenz \(1/T\) des periodischen Signals?
Welche Dimension hat die Systemmatrix für \(f_n(t)\)?
Berechnen Sie die Systemmatrix für \(f_5(t)\) mit \(\omega=1\).
Welche Dimension hat die Normalgleichung?
Lösen Sie mit Hilfe der Cholesky-Zerlegung aus NumPy
```
from np.linalg import cholesky

L = cholesky(A)
```
In matlab
```
L = chol(A,"lower")
```
die Normalgleichung. Wie lautet \(f_n(t)\)?

Achtung: Da \(L\) nicht normiert ist, erfordert das Vorwärtseinsetzen die Division durch das Diagonalelement. In der native SciPy Implementierung wird dies gemacht.
```
from scipy.linalg import solve_triangular
```
In matlab
```
opts.LT = true;
x = linsolve(L,b,opts);
```
Visualisieren Sie Ihre Lösung in den Messdaten. Welche Anteile sind massgebend vorhanden? (Optional: Vergleichen Sie das Resultat mit der FFT.)
Wie gross ist die quadratische Fehlersumme?

(Optional für Python interessierte Studierende nach der Bearbeitung des Auftrag 2!) Vervollständigen Sie die python Klasse mit Funktionalität.

Initialisierung speichert die Messdaten

computeCoefs(n) berechnet und speichert die Koeffizienten für das Modell \(f_n(t)\).

compute(t) berechnet für ein np.array die Modellfunktionen mit den berechneten Koeffizienten.

Sie können sich an der folgenden Vorlage orientieren:

class myFit:
  def __init__(self, data):
      self.setData(data)
      self.c = None       # Klassen Variable für die Modell Koeffizienten
      self.omega = omega

  def setData(self, data):
      self.ti = data[:,0] # Zeitstempel
      self.ui = data[:,1] # Messwerte

  def computeCoefs(self, n=5):
      self.n = n

      <<snipp>>

      self.c = <<snipp>>

  def compute(self,t):
      if not type(mf.c) == np.ndarray:
          self.computeCoefs()

      y = <<snipp>>

      return y

Damit können wir Messdaten effizient analysieren:

# Objekt instanzieren
mf = myFit(data)
# Koeffizienten berechnen
mf.computeCoefs(5)
# Visualisieren
plt.plot(t,mf.compute(t))
plt.show()

Auftrag 2¶

Gegeben ist die Entladungskurve eines RC-Netzwerk Kondensators mit der Kapazität \(C\). Der Innenwiderstand \(R_C\) beträgt \(R_C=100\Omega\).

Zeit [ms]

Spannung [V]

0.0

5.0

0.03

2.94

0.05

1.73

0.08

1.01

0.10

0.6

Bestimmen Sie mit Hilfe eines \(RC\)-Glieds und der linearen Ausgleichsrechnung die Kapazität \(C\) des Kondensators.

Wie lautet die Differentialgleichung? Berechnen Sie die allgemeine Lösung als Basis für das Modell.
Wie lautet die Systemmatrix?
Wie gross ist die Kapazität?

Abgabe¶

Auftrag 1: Lösungsfunktion mit Koeffizienten, Graph mit Messung und Modell, quadratische Fehlersumme.
Auftrag 2: Modell, Kapazität.

Kurzer Bericht mit den Ergebnisse und python Code als Textfile.