Anwendung der Euler Verfahren auf ein Modellproblem

import numpy as np
import matplotlib.pyplot as plt

Wir betrachten das Modellproblem

\[\begin{split}\begin{split}y'(x) & = \lambda y(x)\\ y(0) & = 1\end{split}\end{split}\]

in der numerischen Umsetzung konkret mit

\[\lambda = -1.\]

In dem Fall ist die analytische Lösung gegeben durch

\[y_a(x) = e^{-x}.\]

def f(x,y):
    return -y

Explizites Euler-Verfahren

Das explizite Euler-Verfahren ist gegeben durch

\[y_{k+1} = y_k + h \cdot (\lambda y_k) = (1+h\cdot \lambda)\cdot y_k\]

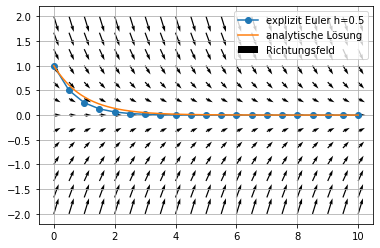
Schrittweite h=0.5

xe = [0]
ye = [1.]
h = 0.5
lam = -1
for k in range(20):
    ye.append((1+h*lam)*ye[-1])
    xe.append(xe[-1]+h)

xp = np.linspace(0,10,200)
plt.plot(xe,ye,'o-',label='explizit Euler h=0.5')
plt.plot(xp,np.exp(-xp),label='analytische Lösung')
xq = h*np.arange(0,len(xe))
yq = np.linspace(-2,2,13)
xq,yq = np.meshgrid(xq,yq)
plt.quiver(xq,yq,np.ones_like(xq),f(xq,yq),angles='xy',label='Richtungsfeld')
plt.legend(loc=1)
plt.grid()
plt.show()

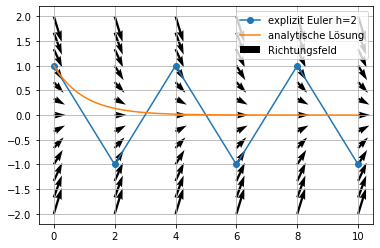
Schrittweite h=2

xe2 = [0]
ye2 = [1.]
h = 2
lam = -1
for k in range(5):
    ye2.append((1+h*lam)*ye2[-1])
    xe2.append(xe2[-1]+h)

plt.plot(xe2,ye2,'o-',label='explizit Euler h=2')
plt.plot(xp,np.exp(-xp),label='analytische Lösung')
xq = h*np.arange(0,len(xe2))
yq = np.linspace(-2,2,13)
xq,yq = np.meshgrid(xq,yq)
plt.quiver(xq,yq,np.ones_like(xq),f(xq,yq),angles='xy',label='Richtungsfeld')
plt.legend(loc=1)
plt.grid()
plt.show()

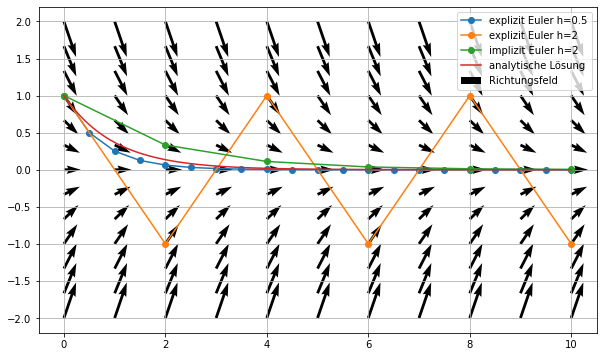
Implizites Euler-Verfahren

Das implizites Euler-Verfahren ist gegeben durch

\[y_{k+1} = y_k + h \cdot (\lambda y_{k+1})\quad \Rightarrow\quad y_{k+1} = \frac{1}{1-h\cdot \lambda}\cdot y_k\]

xi = [0]
yi = [1.]
h = 2
lam = -1
for k in range(5):
    yi.append(1/(1-h*lam)*yi[-1])
    xi.append(xi[-1]+h)

plt.figure(figsize=(10,6))
xp = np.linspace(0,10,200)
plt.plot(xe,ye,'o-',label='explizit Euler h=0.5')
plt.plot(xe2,ye2,'o-',label='explizit Euler h=2')
plt.plot(xi,yi,'o-',label='implizit Euler h=2')
plt.plot(xp,np.exp(-xp),label='analytische Lösung')
xq = h/2*np.arange(0,2*len(xi)-1)
yq = np.linspace(-2,2,13)
xq,yq = np.meshgrid(xq,yq)
plt.quiver(xq,yq,np.ones_like(xq),f(xq,yq),angles='xy',label='Richtungsfeld')
plt.grid()
plt.legend()
plt.show()

Frage: Was passiert mit \(h=1\) für das explizite Euler-Verfahren?