Verfahren nach Hammer und Hollingsworth

Butcher-Tableu - 2-stufiges RK Verfahren

Das Verfahren nach Hammer und Hollingsworth ist durch das folgende Butcher-Tableau gegeben:

\[\begin{split}\begin{array}{c|cc} c & A\\\hline & b^T \end{array} = \begin{array}{c|cc} \frac{3-\sqrt{3}}{6} & \frac{1}{4} & \frac{1}{4}-\frac{1}{6}\sqrt{3} \\ \frac{3+\sqrt{3}}{6} & \frac{1}{4}+\frac{1}{6}\sqrt{3} & \frac{1}{4} \\\hline & \frac{1}{2} & \frac{1}{2} \end{array}\end{split}\]

Das Verfahren wird in der Literatur auch als implizit Runge-Kutta-Gauss Verfahren bezeichnet. Das Verfahren basiert auf der Gauss-Quadratur. Für \(m=1\) folgt auf dem Intervall \([-1,1]\) für die Knoten \(\xi_{1,2}=\mp\sqrt{3}/3\) (vgl. Jupyter-Notebook Quadratur-Formeln). Auf das Intervall \([0,1]\) bezogen, erhalten wir

\[\xi_{1,2}=\frac{1}{2}+\mp\frac{\sqrt{3}}{2\cdot 3} = \frac{3\mp \sqrt{3}}{6}.\]

Damit folgt:

\begin{equation*}\begin{array}{c|cc|l|l} m & b & \xi & \text{Verfahren} & \text{Konsistenzordnung}\\\hline m=0 & b_1 = 1 & \xi_1 = \frac{1}{2} & \text{implizite Mittelpunkt-Regel}&2\\ m=1 & b_1 = b_2 = \frac{1}{2} &\xi_1 = \frac{3- \sqrt{3}}{6},\ \xi_1 = \frac{3+ \sqrt{3}}{6} & \text{implizit Hammer-Hollingsworth Verfahren}&4\\ \end{array}\end{equation*}

Die Gewichte der \(A\) Matrix des Butcher-Tableaus ergeben sich durch Integration der Lagrange Interpolationspolynome 1. Ordnung definiert durch die Stützstellen \(\xi_1,\xi_2\) auf den Intervalle \([0,\xi_1], [0,\xi_2]\):

import numpy as np
import matplotlib.pyplot as plt
import sympy as sp
from sympy import init_printing
init_printing()

xi = [(3-sp.sqrt(3))/6,(3+sp.sqrt(3))/6]
id2 = np.eye(2)
s = sp.symbols('s')
basispolynome=[(s-xi[1])/(xi[0]-xi[1]), (s-xi[0])/(xi[1]-xi[0])]

basispolynome

$\displaystyle \left[ - \sqrt{3} \left(s - \frac{1}{2} - \frac{\sqrt{3}}{6}\right), \ \sqrt{3} \left(s - \frac{1}{2} + \frac{\sqrt{3}}{6}\right)\right]$

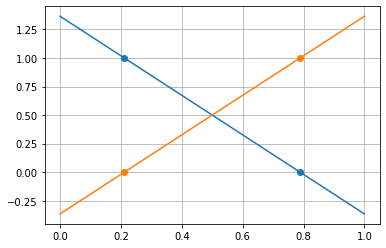
xp = np.linspace(0,1,10)
for b,c in zip(basispolynome,['tab:blue','tab:orange']):
    plt.plot(xp,sp.lambdify(s,b)(xp),c=c)
    plt.plot(xi,sp.lambdify(s,b)(np.array(xi)),'o',c=c)
plt.grid()

[[sp.simplify(sp.integrate(b,(s,0,xii))) for xii in xi] for b in basispolynome]

$\displaystyle \left[ \left[ \frac{1}{4}, \ \frac{1}{4} + \frac{\sqrt{3}}{6}\right], \ \left[ \frac{1}{4} - \frac{\sqrt{3}}{6}, \ \frac{1}{4}\right]\right]$

In der Stufenform

\[\begin{split}\begin{split} k_1 & = y_k + h\, (a_{1 1} f(x_k+c_1\,h, k_1) + a_{1 2} f(x_k+c_2\,h, k_2))\\ k_2 & = y_k + h\, (a_{2 1} f(x_k+c_1\,h, k_1) + a_{2 2} f(x_k+c_2\,h, k_2))\\ y_{k+1} & = y_k + h\, (b_1 f(x_k+c_1\,h, k_1) + b_2 f(x_k+c_2\,h, k_2)) \end{split}\end{split}\]

folgt für das Verfahren

\[\begin{split}\begin{split} k_1 & = y_k + h\, \left(\frac{1}{4}\cdot f\left(x_k+\frac{3-\sqrt{3}}{6}\,h, k_1\right) + \frac{3-2\sqrt{3}}{12}\cdot f\left(x_k+\frac{3+\sqrt{3}}{6}\,h, k_2\right)\right)\\ k_2 & = y_k + h\, \left(\frac{3+2\sqrt{3}}{12}\cdot f\left(x_k+\frac{3-\sqrt{3}}{6}\,h, k_1\right) + \frac{1}{4}\cdot f\left(x_k+\frac{3+\sqrt{3}}{6}\,h, k_2\right)\right)\\ y_{k+1} & = y_k + \frac{1}{2}\cdot h\, \left( f\left(x_k+\frac{3-\sqrt{3}}{6}\,h, k_1\right) + f\left(x_k+\frac{3+\sqrt{3}}{6}\,h, k_2\right)\right) \end{split}\end{split}\]

In der Steigungsform (auch Standardform)

\[\begin{split}\begin{split} r_1 & = f\big(x_k+ c_1 h, y_k + h\, (a_{1,1}\, r_1 + a_{1,2}\, r_2)\big)\\ r_2 & = f\big(x_k+ c_2 h, y_k + h\, (a_{2,1}\, r_1 + a_{2,2}\, r_2)\big)\\ y_{k+1} & = y_{k} + h\, (b_1\, r_1 + b_2\, r_2). \end{split}\end{split}\]

folgt für das Verfahren

\[\begin{split}\begin{split} r_1 & = f\big(x_k+ \frac{3-\sqrt{3}}{6} h, y_k + h\, (\frac{1}{4}\, r_1 + \big(\frac{1}{4}-\frac{1}{6}\sqrt{3}\big)\, r_2)\big)\\ r_2 & = f\big(x_k+ \frac{3+\sqrt{3}}{6} h, y_k + h\, (\big(\frac{1}{4}+\frac{1}{6}\sqrt{3}\big)\, r_1 + \frac{1}{4}\, r_2)\big)\\ y_{k+1} & = y_{k} + \frac{h}{2}\, (r_1 + r_2). \end{split}\end{split}\]

Bemerkung: Bei diesem Verfahren wird der numerische Vorteil der Steigungsform gut sichtbar. In der Stufenform werden 4 Funktionsauswertungen \(f(x,y)\) für die Stufen \(k_{1,2}\) und zwei für die Integration benötigt. In der Steigungsform sind es gerade die zwei Steigungen, daher 2 versus 6!

Umsetzung der Steigungsform

from scipy.linalg import lu, solve_triangular

Wir berechnen mit Hilfe des Hammer-Hollingsworth Verfahren Lösungen für \(x\in [0,1]\) des Anfangswertproblems

\[y'(x) = -4 y(x)\qquad y(0) = 1.\]

Die analytische Lösung ist gegeben durch \(y_a(x) = e^{-4x}\).

def f(x,y):
    return -4.*y
def df(x,y):
    return -4.

def ya(x):
    return np.exp(-4*x)

In jedem Zeitschritt müssen wir das (nichtlineare) Gleichungssystem

\begin{equation}\begin{split} r_1 & = f\big(x_k+ \frac{3-\sqrt{3}}{6} h, y_k + h\, (\frac{1}{4}\, r_1 + \big(\frac{1}{4}-\frac{1}{6}\sqrt{3}\big)\, r_2)\big)\\ r_2 & = f\big(x_k+ \frac{3+\sqrt{3}}{6} h, y_k + h\, (\big(\frac{1}{4}+\frac{1}{6}\sqrt{3}\big)\, r_1 + \frac{1}{4}\, r_2)\big) \end{split}\end{equation}

für die Steigungen \(r_1, r_2\) berechnen. Dadurch, dass die beiden Steigungen in beiden Gleichungen vorkommen, müssen wir ein nichtlineares Gleichungssystem lösen, was das Verfahren insbesondere für Differentialgleichungssysteme numerisch teuer macht.

Für die generische Funktion \(G(r)\) für das Newton-Verfahren folgt \begin{equation}G(r) = \begin{pmatrix} r_1 - f\big(x_k+ \frac{3-\sqrt{3}}{6} h, y_k + h\, (\frac{1}{4}\, r_1 + \big(\frac{1}{4}-\frac{\sqrt{3}}{6}\big)\, r_2)\big)\\ r_2 - f\big(x_k+ \frac{3+\sqrt{3}}{6} h, y_k + h\, (\big(\frac{1}{4}+\frac{\sqrt{3}}{6}\big)\, r_1 + \frac{1}{4}\, r_2)\big) \end{pmatrix}.\end{equation} Die Jacobi-Matrix ist gegeben durch \begin{equation}G'(r) = \mathbb{1} - h\,\begin{pmatrix} \frac{1}{4}\partial_y f\big(x_k+ \frac{3-\sqrt{3}}{6} h, y_k + h\, (\frac{1}{4}\, r_1 + \big(\frac{1}{4}-\frac{\sqrt{3}}{6}\big)\, r_2)\big) & \left(\frac{1}{4}-\frac{\sqrt{3}}{6}\right)\partial_y f\big(x_k+ \frac{3-\sqrt{3}}{6} h, y_k + h\, (\frac{1}{4}\, r_1 + \big(\frac{1}{4}-\frac{\sqrt{3}}{6}\big)\, r_2)\big)\\ \left(\frac{1}{4}+\frac{\sqrt{3}}{6}\right)\partial_y f\big(x_k+ \frac{3+\sqrt{3}}{6} h, y_k + h\, (\big(\frac{1}{4}+\frac{\sqrt{3}}{6}\big)\, r_1 + \, r_2) & \frac{1}{4}\partial_y f\big(x_k+ \frac{3+\sqrt{3}}{6} h, y_k + h\, (\big(\frac{1}{4}+\frac{\sqrt{3}}{6}\big)\, r_1 + \, r_2)\big) \end{pmatrix}.\end{equation}

def implizitHammerHollingsworth(xend, h, y0, f, df):
    x = [0.]
    y = [y0]
    cHH = np.array([(3-np.sqrt(3))/6,(3+np.sqrt(3))/6])
    aHH = np.array([[1/4,(1/4-np.sqrt(3)/6)],[(1/4+np.sqrt(3)/6),1/4]])
    bHH = np.array([0.5,0.5])
    id2 = np.eye(2)

    # Verfahrensfunktion für implizit Euler
    def G(r, xk, yk):
        return np.array([r[0]-f(xk+cHH[0]*h, yk+h*(aHH[0,:]@r)),
                         r[1]-f(xk+cHH[1]*h, yk+h*(aHH[1,:]@r))])

    # Partielle Ableitung nach s der Verfahrensfunktion
    def dG(r, xk, yk):
        return id2-h*np.array([df(xk+cHH[0], yk+h*(aHH[0,:]@r))*aHH[0,:],
                               df(xk+cHH[1], yk+h*(aHH[1,:]@r))*aHH[1,:]])

    # Newton-Verfahren für Steigung
    def newton(r, xk, yk, tol=1e-12, maxIter=20):
        k = 0
        delta = np.ones_like(r)*10*tol
        while np.linalg.norm(delta,np.inf) > tol and k < maxIter:
            # LR-Zerlegung
            A = dG(r,xk, yk)
            b = G(r,xk,yk)
            P,L,R = lu(A)
            z = solve_triangular(L,P.T@b,lower=True) # Vorwärtseinsetzen
            delta = solve_triangular(R,z,lower=False) # Rückwärtseinsetzen
            r -= delta
            k += 1
        return r

    # Zeitloop
    r = np.array([f(x[-1],y[-1]),f(x[-1],y[-1])])
    while x[-1] < xend-h/2:
        r = newton(r,x[-1],y[-1])
        y.append(y[-1]+h*r@bHH)
        x.append(x[-1]+h)
    return np.array(x), np.array(y)

x,y = implizitHammerHollingsworth(1,0.1,1,f,df)

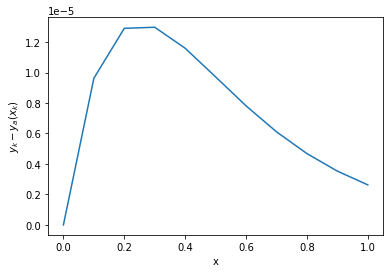
plt.plot(x,y-ya(x))
plt.xlabel('x')
plt.ylabel('$y_k-y_a(x_k)$')
plt.show()

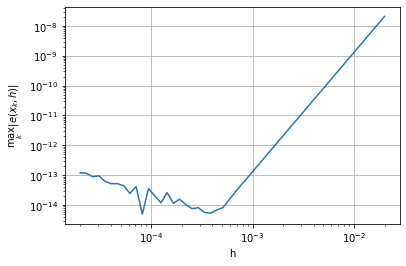
Kontrolle Konvergenzordnung

n = 10**np.linspace(2,5)
hs = 2/n
err = []
for h in hs:
    x, y = implizitHammerHollingsworth(1,h,1,f,df)
    err.append(np.linalg.norm(y-ya(x),np.inf))

plt.loglog(hs,err,'-')
plt.xlabel('h')
plt.ylabel(r'$\max_k \|e(x_k,h)\|$')
plt.grid()
plt.show()

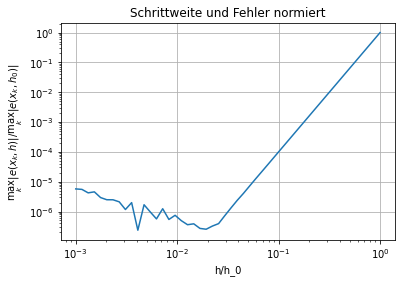
Um die Konvergenzordnung leicht aus dem Diagram lesen zu können, normieren wir die Schrittweiten und Fehler:

plt.loglog(hs/hs[0],err/err[0],'-')
plt.xlabel('h/h_0')
plt.ylabel(r'$\max_k \|e(x_k,h)\|/\max_k \|e(x_k,h_0)\|$')
plt.grid()
plt.title('Schrittweite und Fehler normiert')
plt.show()