Quadratur Formeln

Achtung: Hintergrundwissen Quadratur Formeln (nicht SEP Inhalt!). Es beinhaltet aber viele interessante Punkte, mathematische wie auch Software technische. In der Umsetzung kommt ein Mix aus Numerik und symbolischem Rechnen mit Hilfe von sympy zur Anwendung. Bitte beachten Sie, dass Befehle wie solve, nsolve in der SEP nicht akzeptiert werden!

Der Fokus liegt auf den sogenannten Quadratur Formeln:

\[Q(f) = h\cdot \sum_{j=1}^s b_j f(\xi_j) \approx \int_{x_k}^{x_{k+1}} f(x) dx\]

Wir betrachten zwei wichtige Zugänge zu den Quadratur Formeln:

• Interpolation der zu integrierenden Funktion mit Hilfe von Lagrange Polynome an fest vorgegeben Stützstellen.

• Optimale Verteilung von Stützstellen im Sinne der maximalen Polynomordnung für eine exakte Integration.

import numpy as np
import matplotlib.pyplot as plt
import sympy as sp
from scipy.interpolate import lagrange
colors=['tab:blue','tab:orange','tab:green','tab:red','tab:purple','tab:brown','tab:pink','tab:gray','tab:olive','tab:cyan']
from ipywidgets import interact
import ipywidgets as widgets

Integration mit Hilfe von Lagrange Polynomen

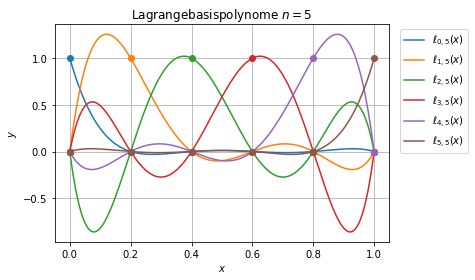
Lagrange Interpolationspolynome

Die Lagrange-Polynominterpolation hat eine eindeutige Lösung \(P_n\in\Pi_n\) gegeben durch

\[P_n(x) = \sum_{j=0}^n f(x_j) \ell_{j\, n}(x),\]

mit

\begin{equation}\label{eq:lagrangepoly}\ell_{j\, n}(x) = \prod_{\substack{k=0\\ k\not= j}}^n \frac{x-x_k}{x_j-x_k}.\end{equation}

Wir betrachten die Lagrangepolynome auf dem Einheitsintervall \([0,1]\).

basispolynome = []
xi = []
yi = []
for p in range(1,6):
    # die Stützstellen werden äquidistant verteilt
    x = np.linspace(0,1,p+1)
    id = np.eye(p+1)
    basispolynome.append([lagrange(x,e) for e in id])
    xi.append(x)
    yi.append(id)

xp=np.linspace(0,1,200)
for p,xii,yii in zip(basispolynome,xi,yi):
    j = 0
    for pi,yiii in zip(p,yii):
        plt.plot(xp,pi(xp),label='$\ell_{'+str(j)+','+str(len(p)-1)+'}(x)$',c=colors[j])
        plt.plot(xii,yiii,'o',c=colors[j])
        j+=1
    plt.title(r'Lagrangebasispolynome $n='+str(len(p)-1)+'$')
    #plt.axhline(0,color='gray')
    #plt.axhline(1,color='gray')
    plt.legend(loc=1,bbox_to_anchor=(1.25,1))
    plt.grid()
    plt.xlabel('$x$')
    plt.ylabel('$y$')
    plt.show()

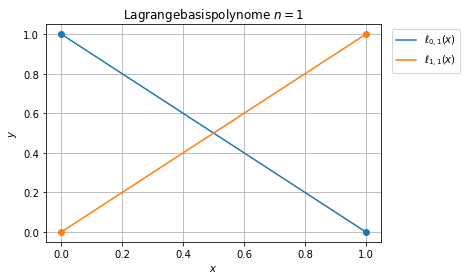
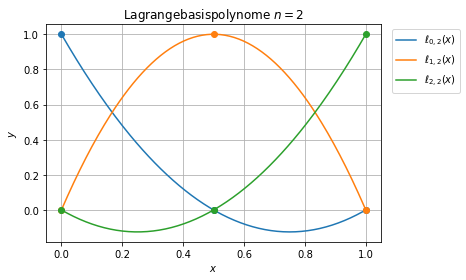
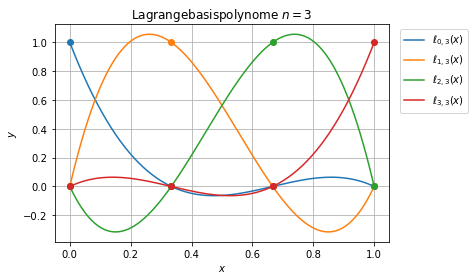
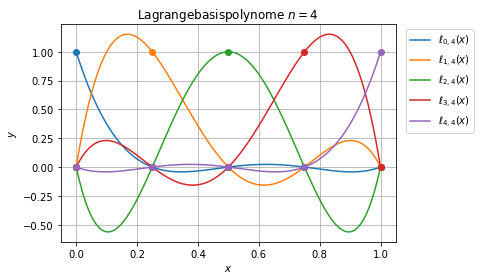
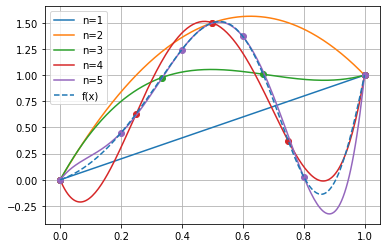
Für die Lagrange-Polynominterpolation

\[P_n(x) = \sum_{j=0}^n f(x_j) \ell_{j\, n}(x),\]

erhalten wir z.B. für die Funktion

\[f(x) = x+\sin(2\pi x^2)\]

auf dem Einheitsintervall die folgenden Interpolationspolynome.

def f(x):
    return x+np.sin(2*np.pi*x**2)

x = sp.symbols('x')

g=[sp.expand(np.sum([f(xi[k][j])*(basispolynome[k][j](x)) for j in range(len(xi[k]))])) for k in range(len(xi))]
j = 1
for gi in g:
    print('Interpolationspolynom Grad n='+str(j)+':')
    display(gi)
    j+=1

Interpolationspolynom Grad n=1:

$\displaystyle 1.0 x$

Interpolationspolynom Grad n=2:

$\displaystyle - 4.0 x^{2} + 5.0 x$

Interpolationspolynom Grad n=3:

$\displaystyle 4.06036079587175 x^{3} - 8.30635863808509 x^{2} + 5.24599784221334 x$

Interpolationspolynom Grad n=4:

$\displaystyle 64.0 x^{4} - 119.836086776211 x^{3} + 63.7541301643171 x^{2} - 6.91804338810571 x$

Interpolationspolynom Grad n=5:

$\displaystyle 113.486167251067 x^{5} - 221.278537875213 x^{4} + 130.873060027612 x^{3} - 25.8473335919819 x^{2} + 3.76664418851616 x$

Erstellen wir aus der Sympy Expressions der Interpolationspolynome aufrufbare Funktionen für die graphische Darstellung.

finterpolated=[sp.lambdify(x,gi) for gi in g]

j=0
for fi in finterpolated:
    plt.plot(xp,fi(xp),label='n='+str(j+1),color=colors[j])
    plt.plot(xi[j],f(xi[j]),'o',color=colors[j])
    j+=1
plt.plot(xp,f(xp),'--',label='f(x)')
plt.legend()
plt.grid()

Newton-Cotes-Formeln

Zurück zur Integration:

\[\int_0^1 f(x) dx \approx \int_0^1 P_n(x) dx = \int_0^1 \sum_{j=0}^n f(x_j) \ell_{j\, n}(x) dx\]

Die Berechnung des Integrals kann nun ohne Kenntnis von \(f(x)\) vorgezogen werden

\[\int_0^1 f(x) dx \approx \int_0^1 \sum_{j=0}^n f(x_j) \ell_{j\, n}(x) dx = \sum_{j=0}^n f(x_j) \int_0^1 \ell_{j\, n}(x) dx\]

da \(f(x_j)\) konstante Faktoren sind, mit dem Ziel eine Quadratur Formel

\[Q(f) = h\cdot \sum_{j=1}^s b_j f(\xi_j) \approx \int_{x_k}^{x_{k+1}} f(x) dx\]

zu erhalten. Damit erhalten wir die Gewichte \(b_j\), wobei in der Quadratur Formel für den Index \(j = 1, \ldots, n+1=s\) gilt.

b = []
for p in basispolynome:
    b.append([sp.integrate(pi(x),(x,0,1)) for pi in p])

j=1
for bj in b:
    print('n='+str(j)+':')
    print(bj)
    j+=1

n=1:
[0.500000000000000, 0.500000000000000]
n=2:
[0.166666666666667, 0.666666666666667, 0.166666666666667]
n=3:
[0.125000000000000, 0.374999999999999, 0.375000000000000, 0.125000000000000]
n=4:
[0.0777777777777793, 0.355555555555558, 0.133333333333333, 0.355555555555554, 0.0777777777777775]
n=5:
[0.0659722222222250, 0.260416666666664, 0.173611111111095, 0.173611111111128, 0.260416666666668, 0.0659722222222214]

n=1: Trapezregel n=2: 2/3-Regel n=3: Simpson-Regel

Bemerkung: Bei diesem Zugang ist die Integrationsordnung nicht optimal. Nicht desto trotz basieren einige numerische Methoden für die Integration von Differentialgleichungen auf diesen Quadratur-Formeln:

n=1: Trapezmethode (implizit) n=2: klassisches Runge-Kutta Verfahren 4. Ordnung (explizit)

Gauss-Quadratur

Bei Newton-Cotes-Formeln höherer Ordnung ergeben sich Gewichte mit wechselnden Vorzeichen. Aufgrund von Auslöschung sind derartige Formeln weniger stabil.

Eine weitere Einschränkung bei den Newton-Cotes-Formeln ist die Festlegung auf äquidistante Stützstellen. Die Frage ist, ob sich nicht die Fehlerordnung hochschrauben liesse, wenn man die Stützstellen freigibt.

Gauss-Quadratur 1. Ordnung

Beispiel: mit n = 1 folgt

\[\int_{-1}^1 f(x) dx \approx 2\cdot (c_0 f(x_0) + c_1 f(x_1))\]

Wir haben daher 4 Parameter, was eine exakte Integration von Polynom bis und mit 3. Grad zulassen sollte.

Daher stellen wir die Gleichungen für \(f(x) = x^k\):

\[\int_{-1}^1 x^k dx \approx 2\cdot (c_0 x_0^k + c_1 x_1^k)\quad k = 0, 1, 2, 3\]

c0,x0,c1,x1 = sp.symbols('c0,x0,c1,x1')

Die Integrationsgrenzen werden in diesem Ansatz symmetrisch gewält, was zu einem einfacher lösbaren nichtlinearen Gleichungssystem führt:

for k in range(4):
    display(sp.Equality(sp.integrate(x**k,(x,-1,1)),2*(c0*x0**k+c1*x1**k)))

$\displaystyle 2 = 2 c_{0} + 2 c_{1}$

$\displaystyle 0 = 2 c_{0} x_{0} + 2 c_{1} x_{1}$

$\displaystyle \frac{2}{3} = 2 c_{0} x_{0}^{2} + 2 c_{1} x_{1}^{2}$

$\displaystyle 0 = 2 c_{0} x_{0}^{3} + 2 c_{1} x_{1}^{3}$

Wir erhalten zwei äquivalente Lösungen:

sp.solve([sp.integrate(x**k,(x,-1,1))-2*(c0*x0**k+c1*x1**k) for k in range(4)])

[{c0: 1/2, c1: 1/2, x0: -sqrt(3)/3, x1: sqrt(3)/3},
 {c0: 1/2, c1: 1/2, x0: sqrt(3)/3, x1: -sqrt(3)/3}]

Mit dem Ansatz könen wir beliebige Polynome 3. Grades exakt integrieren, was schon sehr verblüffend ist!

def f(x):
    return 1+x+x**2-x**3

sp.integrate(f(x),(x,-1,1))

$\displaystyle \frac{8}{3}$

Mit Hilfe der Quadratur-Formel erhalten wir:

2*(0.5*f(-np.sqrt(3)/3)+0.5*f(np.sqrt(3)/3))

2.6666666666666665

Diese Quadratur Formel findet Anwendung zum Integrieren von Differentialgleichugen im Verfahren nach Hammer und Hollingsworth, ein voll implizites zwei stufiges Runge-Kutta Verfahren mit optimaler Konvergenzordnung.

Gaus-Quadratur höherer Ordnung

s=sp.symbols('s')

m=3
c = sp.symbols('c:'+str(m))
x = sp.symbols('x:'+str(m))
sol=sp.solve([sp.integrate(s**k,(s,-1,1))-2*np.sum([c[i]*x[i]**k for i in range(m)]) for k in range(2*m)])
sol

[{c0: 5/18, c1: 5/18, c2: 4/9, x0: -sqrt(15)/5, x1: sqrt(15)/5, x2: 0},
 {c0: 5/18, c1: 5/18, c2: 4/9, x0: sqrt(15)/5, x1: -sqrt(15)/5, x2: 0},
 {c0: 5/18, c1: 4/9, c2: 5/18, x0: -sqrt(15)/5, x1: 0, x2: sqrt(15)/5},
 {c0: 5/18, c1: 4/9, c2: 5/18, x0: sqrt(15)/5, x1: 0, x2: -sqrt(15)/5},
 {c0: 4/9, c1: 5/18, c2: 5/18, x0: 0, x1: -sqrt(15)/5, x2: sqrt(15)/5},
 {c0: 4/9, c1: 5/18, c2: 5/18, x0: 0, x1: sqrt(15)/5, x2: -sqrt(15)/5}]

Die Lösung 2 ist in der gewünschten Reihenfolge:

sol[2]

{c0: 5/18, c1: 4/9, c2: 5/18, x0: -sqrt(15)/5, x1: 0, x2: sqrt(15)/5}

Mit der Quadratur Formel

\[Q(g) = 2\cdot\left(\frac{5}{18} g(-\sqrt{15}/5) + \frac{4}{9} g(0) + \frac{5}{18} g(\sqrt{15}/5)\right)\]

können Polynome bis 5. Grad exakt integriert werden:

def Q(g):
    return 2*np.sum([sol[2][c[k]]*g(sol[2][x[k]]) for k in range(len(c))])

p=sp.random_poly(s,5,-10,10)
p

$\displaystyle 7 s^{5} - 5 s^{3} + 8 s^{2} - 3 s - 10$

analytisches Resultat:

sp.integrate(p,(s,-1,1))

$\displaystyle - \frac{44}{3}$

Resultat mit Quadratur Formel:

Q(sp.lambdify(s,p))

$\displaystyle - \frac{44}{3}$

Mit scypy können weitere Koeffizienten nicht mehr algebraisch gelöst werden. In Mathematica kann die Rechnung bis ca. m=8 fortgesetzt werden. Unabhängig davon macht es Sinn, die Lösungen numerisch zu berechnen. Die Stützstellen sind irrational und werden in der Regel in einer Lookup Tabelle zur Verfügung gestellt.

sp.nsolve([sp.integrate(s**k,(s,-1,1))-2*np.sum([c[i]*x[i]**k for i in range(m)]) for k in range(2*m)],
          (*x,*c),
          (*np.linspace(-1,1,3),*np.ones(3)/3))

$\displaystyle \left[\begin{matrix}-0.774596669241483\\6.05845175209737 \cdot 10^{-27}\\0.774596669241483\\0.277777777777778\\0.444444444444444\\0.277777777777778\end{matrix}\right]$

sp.N(sol[2][x[2]])

$\displaystyle 0.774596669241483$

m=4
c = sp.symbols('c:'+str(m))
x = sp.symbols('x:'+str(m))
sol=sp.nsolve([sp.integrate(s**k,(s,-1,1))-2*np.sum([c[i]*x[i]**k for i in range(m)]) for k in range(2*m)],
          (*x,*c),
          (*np.linspace(-1+1/m**2,1-1/m**2,m),*np.ones(m)/m))
print('x_i=',sol[:m])
print('c_i=',sol[m:])

x_i= [-0.861136311594053, -0.339981043584856, 0.339981043584856, 0.861136311594053]
c_i= [0.173927422568727, 0.326072577431273, 0.326072577431273, 0.173927422568727]

Polynomgrad mit exakter Integration:

2*m-1

7

m=5
c = sp.symbols('c:'+str(m))
x = sp.symbols('x:'+str(m))
sol=sp.nsolve([sp.integrate(s**k,(s,-1,1))-2*np.sum([c[i]*x[i]**k for i in range(m)]) for k in range(2*m)],
          (*x,*c),
          (*np.linspace(-1+1/m**2,1-1/m**2,m),*np.ones(m)/m))
print('x_i=',sol[:m])
print('c_i=',sol[m:])

x_i= [-0.906179845938664, -0.538469310105683, -2.41385608130116e-21, 0.538469310105683, 0.906179845938664]
c_i= [0.118463442528095, 0.239314335249683, 0.284444444444444, 0.239314335249683, 0.118463442528095]

Polynomgrad mit exakter Integration:

2*m-1

9

Integration über ein beliebiges Intervall

Bis hier hin haben wir die Integration über das Referenzintervall \([0,1]\) bzw. \([-1,1]\) betrachtet. Abschliessend betrachten wir nun die Integration über ein beliebiges Intervall \([a,b]\):

\[\int_a^b f(x) dx.\]

Dazu gehen wir wie folgt vor:

1. Unterteile \([a,b]\) in Teilintervalle \([x_{k-1},x_k]\)

2. Approximiere das Teilintegral auf jedem Intervall \([t_{k-1},t_k]\) mit einer Quadratur Formel

3. Summieren liefert

   \[\int_a^bf(x) dx = \sum_{k=1}^n \int_{t_{k-1}}^{t_k} f(x) dx \approx \sum_{k=1}^n h_k\cdot \sum_{j=1}^s b_j f(\xi_j)\]

Das einzige was noch zu definieren ist, ist die Position der Funktionauswertung \(\xi_j\). Die Integratinspunkte sind durch die Quadratur Formel gegeben auf dem Referenzintervall. Wir bezeichnen nun die Integrationspunkte im Referenzintervall mit \(c_j\), dann folgt

• Referenzintervall \([0,1]\): \(\xi_j = x_k + h_k \cdot c_j\)

• Referenzintervall \([-1,1]\): \(\xi_j = x_k + \frac{h_k}{2} \cdot (1+c_j)\)

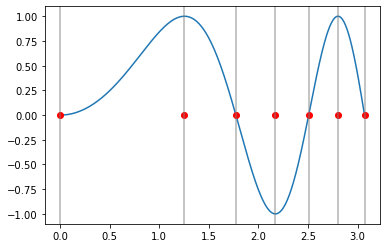
Wir betrachten folgende Beispiel:

\[\int_0^{\sqrt{3\pi}} \sin(x^2) dx\]

Iexakt = float(sp.N(sp.integrate(sp.sin(s**2),(s,0,(3*np.pi)**0.5))))
Iexakt

0.7882589655667055

def f(x):
    return np.sin(x**2)

Die Teilintervalle wählen wir nicht äquidistant, so dass die Grenzen jeweilen im Nulldurchgang bzw. in den Extremalpunkte liegen.

xp = np.linspace(0,(3*np.pi)**0.5,400)
xi = np.sqrt(np.linspace(0,(3*np.pi),7))
plt.plot(xp,f(xp))
plt.plot(xi,np.zeros_like(xi),'ro')
for x in xi:
    plt.axvline(x,c='gray',alpha=0.6)

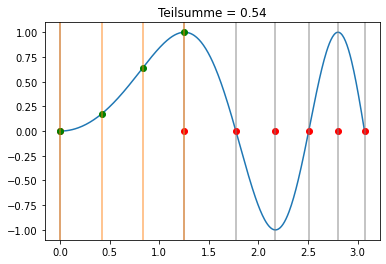
Newton-Cotes Formel

Wir benutzen nun die Simpson-Regel in jedem Teilintervall:

bS = np.array([1/8, 3/8, 3/8, 1/8])
cS = np.linspace(0,1,bS.shape[0])
xi = np.sqrt(np.linspace(0,(3*np.pi),7))

def visualize(k,b,c,xi,trafo):
    hk = (xi[k+1]-xi[k])
    s = hk*f(trafo(xi[k],hk,c))@b

    plt.plot(xp,f(xp))
    plt.plot(xi,np.zeros_like(xi),'ro')
    for x in xi:
        plt.axvline(x,c='gray',alpha=0.6)
    plt.plot(trafo(xi[k],hk,c),f(trafo(xi[k],hk,c)),'go')
    for x in trafo(xi[k],hk,c):
        plt.axvline(x,c='tab:orange',alpha=0.6)
    plt.title('Teilsumme = '+str(np.round(s,3)))
    plt.show()

interact(lambda k: visualize(k,bS,cS,xi,lambda x,h,c: x+h*c), k=widgets.IntSlider(min=0, max=xi.shape[0]-2, step=1, value=0));

for k in range(xi.shape[0]-1):
    visualize(k,bS,cS,xi,lambda x,h,c: x+h*c)

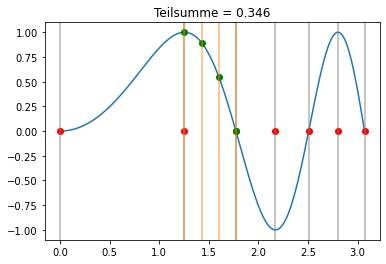
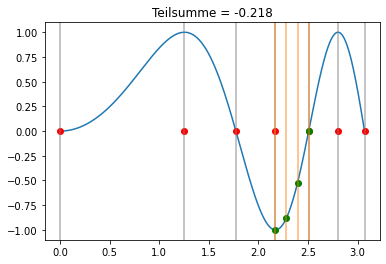
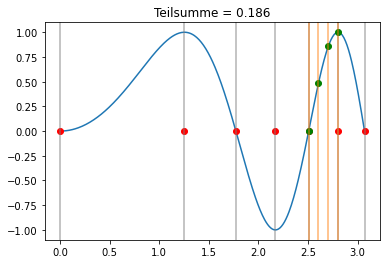
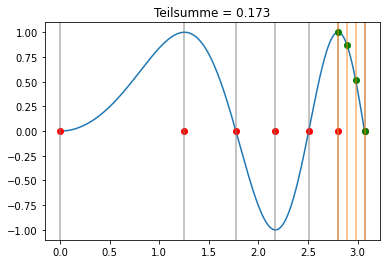
Für das Integral folgt in dem Fall:

ISimpson = 0
for k in range(xi.shape[0]-1):
    hk = (xi[k+1]-xi[k])
    ISimpson += hk*f(xi[k]+hk*cS)@bS
ISimpson

0.7800407349978202

Der absolute Fehler beträgt mit dieser Diskretisierung und Quadratur Formel:

ISimpson-Iexakt

-0.008218230568885265

Gauss-Quadratur

Wir benutzen nun die Gauss-Quadratur m=3 in jedem Teilintervall:

bG = np.array([5/18,4/9,5/18])
cG = np.array([-np.sqrt(15)/5,0,np.sqrt(15)/5])

interact(lambda k: visualize(k,bG,cG,xi,lambda x,h,c: x+h/2*(1+c)), k=widgets.IntSlider(min=0, max=xi.shape[0]-2, step=1, value=0));

for k in range(xi.shape[0]-1):
    visualize(k,bG,cG,xi,lambda x,h,c: x+h/2*(1+c))

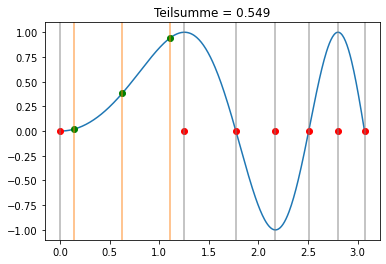
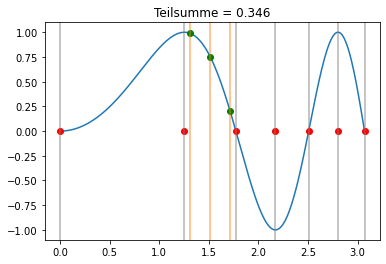
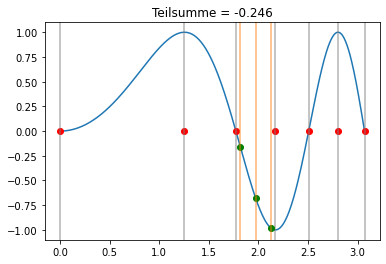
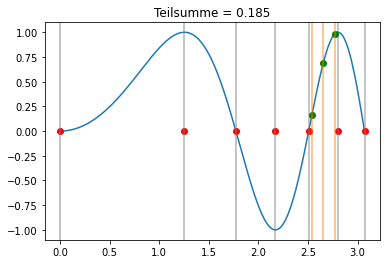
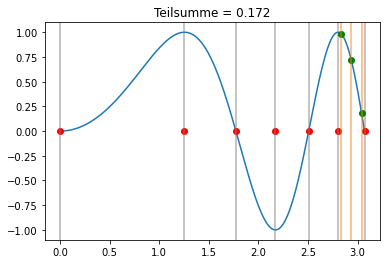
Der Unterschied zwischen den Newton-Cotes Formeln und der Gauss-Quadratur ist auch gut sichtbar darin, dass bei der Gauss-Quadratur nur Punkte innerhalb der Teilintervalle ausgewertet werden.

Für das Integral folgt in dem Fall:

IGauss = 0
for k in range(xi.shape[0]-1):
    hk = (xi[k+1]-xi[k])
    IGauss += hk*f(xi[k]+hk/2*(1+cG))@bG
IGauss

0.7879919336252061

Der absolute Fehler beträgt mit dieser Diskretisierung und Quadratur Formel:

IGauss-Iexakt

-0.0002670319414993516

Im Vergleich nochmals der Fehler mit der Simpson-Regel:

ISimpson-Iexakt

-0.008218230568885265

Das Resultat der Simpson-Regel ist bedeutend schlechter als das der Gauss-Quadratur, obwohl eine Stützstelle weniger benutzt wurde.