Grundlagen der Numerik

Lernziele

1. Sie kennen die unterschiedlichen Fehlerarten, welche in der Numerik zum Tragen kommen.

2. Sie kennen Differenzenquotienten zur Approximation von Ableitungen unterschiedlicher Ordnung.

3. Sie können die Fehlerordnung eines Differenzenquotienten experimentell und analytisch bestimmen.

4. Sie können die optimale Schrittweite eines Differenzenquotienten experimentell bestimmen.

Theorie

Differenzenquotienten zur Approximation von Ableitungen

Bei der numerischen Ableitung einer Funktion \(f(x)=y\) an eienr Stelle \(x_0 \in D_f\) wird der Grenzwert

\[f'(x_0)=\lim\limits_{h \rightarrow 0} \frac{f(x_0+h)-f(x_0)}{h}\]

durch die Sekantensteigung ersetzt

\[f'(x_0) \approx \frac{f(x_0+h)-f(x_0)}{h}\]

\(h>0\) nennen wir die Schrittweite.

Wir bestimmen die Fehlerordnung des mathematischen Verfahrens mit Hilfe der Taylorreihenentwicklung von \(f\):

\[f(x_0+h) = f(x_0) + f'(x_0)h + \frac{f''(x_0)}{2}h^2 + \frac{f^{(3)}(x_0)}{6}h^3 + {\cal O}(h^4)\]

Durch Umformen dieser Gleichung erhalten wir

\[\frac{f(x_0+h)-f(x_0)}{h} - f'(x_0) = \frac{f''(x_0)}{2}h + \frac{f^{(3)}(x_0)}{6}h^2 + {\cal O}(h^3) = {\cal O}(h)\]

Somit hat der Vorwärts-Differenzenquotient \(\displaystyle{\Delta_{h\rightarrow}^1=\frac{f(x_0+h)-f(x_0)}{h}}\) die Fehlerordnung 1, d.h. der Fehler hängt linear von der Schrittweite ab.

Weitere Differenzenquotienten für die Approximation der ersten Ableitung sind

• Rückwärts-Differenzenquotient: \(\displaystyle{\Delta_{h\leftarrow}^1=\frac{f(x_0)-f(x_0-h)}{h}}\) mit Fehlerordnung 1 und

• zentraler Differenzenquotient: \(\displaystyle{\Delta_{2h}^1=\frac{f(x_0+h)-f(x_0-h)}{2h}}\) mit Fehlerordnung 2.

Das folgende Beispiel zeigt, dass neben dem Verfahrensfehler eine weitere Fehlerart zu berücksichtigen ist:

import numpy as np
import matplotlib.pyplot as plt

Wir betrachten die Funktion

\[f(x) = \cos(x)\]

def f(x):
    return np.cos(x)

im Punkt

\[x_0=1.\]

x0 = 1

Wir berechnen nun die Differenzenquotienten mit unterschiedlichen Schrittweiten:

# exakter Wert der Ableitung
y = -np.sin(1)

DeltaRechts = []
DeltaLinks = []
DeltaZentral = []
Hs = 10.**np.arange(-20,-1) # logarithmische Schrittweite

for h in Hs:
    # Fehler des rechtsseitigen Differenzenquotient
    DeltaRechts.append(np.abs(y-(f(x0+h)-f(x0))/h))

    # Fehler des linksseitigen Differenzenquotient
    #DeltaLinks.append(<<snipp selber machen>>)

    # Fehler des zentralen Differenzenquotient
    #DeltaZentral.append(<<snipp selber machen>>)

Für die Analyse betrachten die Logarithmische Darstellung:

plt.loglog(Hs,DeltaRechts,'o-',label='Vorwaertsdifferenzenquotient')
# die beiden folgenden Zeilen können Sie nach dem Implementieren
# der weiteren Differenzenquotienten aktivieren
#plt.loglog(Hs,DeltaLinks,'.-',label='Rueckwaertsdifferenzenquotient')
#plt.loglog(Hs,DeltaZentral,'.-',label='zentraler DiffQuotient')
plt.xlabel('Schrittweite')
plt.ylabel('absoluterFehler')
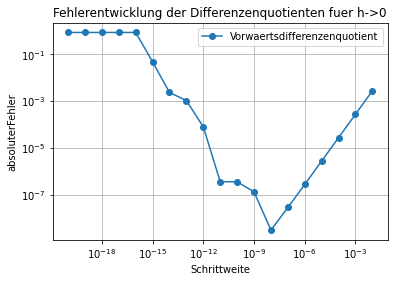
plt.title('Fehlerentwicklung der Differenzenquotienten fuer h->0')
plt.legend()
plt.grid()
plt.show()

Aufträge

1. Analysieren Sie das Ergebnisse des obigen Beispiels. Welche Fehlerarten sind hier zu beobachten? Was folgern Sie daraus?

2. Implementieren Sie die Berechnung des Rueckwaerts- und zentralen Differenzenquotienten.

3. Leiten Sie mit Hilfe der Taylorreihe die Fehlerordnung für den zentralen Differenzenquotienten her (analog zur Einführung).

4. Effiziente Programmierung in Skript-Sprachen: Wie könnte man die obige for-Schleife vermeiden?

Abgabe

Bitte geben Sie Ihre Lösungen bis spätestens vor dem nächsten Praktikum 2 ab.