12.1. Beispiel nichtlineares Randwertproblem

Als Beispiel betrachten wir das folgende nichtlineare Randwertproblem

\[\begin{split}\begin{split}-u''(x) + u(x)^3 & = -3+\frac{1}{8}(4-7 x+3 x^2)^3\\ u(0) & = 2\\ u(2) & = 1.\end{split}\end{split}\]

Die exakte Lösung ist gegeben durch

\[u_{\text{exact}} = \frac{1}{2} (4-7 x+3 x^2).\]

from netgen.meshing import Mesh as NGMesh
from netgen.meshing import MeshPoint, Element0D, Element1D, Pnt
from ngsolve import *

import matplotlib.pyplot as plt
import numpy as np

1D Mesh erstellen: (2 Elemente mit Intervall Länge 2)

# generate a 1D mesh
ngmesh = NGMesh()
ngmesh.dim = 1

nel = 1
l0 = 2

pnums = []
for i in range(0, nel+1):
    pnums.append (ngmesh.Add(MeshPoint (Pnt(i/nel*l0, 0, 0))))

for i in range(0,nel):
    ngmesh.Add (Element1D([pnums[i],pnums[i+1]], index=1))

ngmesh.Add (Element0D(pnums[0], index=1))
ngmesh.Add (Element0D(pnums[nel], index=2))

mesh = Mesh(ngmesh)

FE-Space und Trial, Test Proxyfunktionen für die Definition der schwachen Gleichung

order = 2
V = H1(mesh, order=order, dirichlet=[1,2])
u = V.TrialFunction()
v = V.TestFunction()
gfu = GridFunction(V)

Durch partielle Integration des ersten Terms und für \(v\in V=H_0^1([0,2])\) gilt

\[F(u) v = \int_0^2u'(x) v'(x)\, dx + \int_0^2u(x)^3 v(x)\,dx - \int_0^2(-3+\frac{1}{8}(4-7 x+3 x^2)^3)\, v(x)\, dx = 0 \quad \forall v \in V\]

a = BilinearForm(V)
a += (grad(u)*grad(v)+u**3*v-(-3+1/8*(4-7*x+3*x*x)**3)*v)*dx

Die Variation von \(F(u)\) ist gegeben durch

\[F'(u)w v = \frac{d}{d\varepsilon} F(u+\epsilon w) v \Big|_{\varepsilon=0} = \int_0^2w'(x) v'(x) + 3\,u(x)^2 w(x) v(x)\, dx \quad \forall w, v \in V\]

a1 = BilinearForm(V)
a1 += (grad(u)*grad(v)+3*gfu**2*u*v)*dx

oder mit Hilfe von Computer Algebra in NGSolve:

a.AssembleLinearization(gfu.vec)

Die Dirichlet Randbedingung wird für den Lösungsvektor gesetzt

u0 = CoefficientFunction([2,1])
gfu.Set(u0,BND)

Mit Hilfe der Newton Iteration wird das System gelöst.

\[F(u)v = 0\quad \forall\ v\in V\]

Algorithm 12.1 (Newton Verfahren)

Given \(u_0\)
for \(n = 0, 1, 2, \ldots\)
\(\qquad r_n = F(u_n)\)
\(\qquad F'(u_n)\cdot \delta u = r_n\)
\(\qquad u_{n+1} = u_n - \delta u\)

Aufgabe

Berechne die Linearisierung von \(F(u)\).

res = gfu.vec.CreateVector()
du  = gfu.vec.CreateVector()

for it in range(10):
    print ("Newton iteration", it)

    # solve linearized problem:
    # F(u_n)
    a.Apply (gfu.vec, res)
    
    # F'(u_n)
    a.AssembleLinearization(gfu.vec)
    # oder alternativ das die selber berechnete Variation
    #a1.Assemble()
    
    # F'(u_n) du = F(u_n)
    du.data = a.mat.Inverse(V.FreeDofs()) * res
    # oder alternativ das die selber berechnete Variation
    #du.data = a1.mat.Inverse(V.FreeDofs()) * res

    # update iteration
    # u_n+1 = u_n - du
    gfu.vec.data -= du

    #stopping criteria
    stopcritval = sqrt(abs(InnerProduct(du,res)))
    print ("<A u",it,", A u",it,">_{-1}^0.5 = ", stopcritval)
    if stopcritval < 1e-13:
        break

Newton iteration 0
<A u 0 , A u 0 >_{-1}^0.5 =  2.63044945649285
Newton iteration 1
<A u 1 , A u 1 >_{-1}^0.5 =  1.1461868091843588
Newton iteration 2
<A u 2 , A u 2 >_{-1}^0.5 =  0.23956338535903238
Newton iteration 3
<A u 3 , A u 3 >_{-1}^0.5 =  0.004330380345703788
Newton iteration 4
<A u 4 , A u 4 >_{-1}^0.5 =  6.498623278264114e-07
Newton iteration 5
<A u 5 , A u 5 >_{-1}^0.5 =  1.444693506846862e-14

def uexact(x):
    return 0.5*(4-7*x+3*x*x)

xi = np.linspace(0,l0,150)
ui = [gfu(xip) for xip in xi]

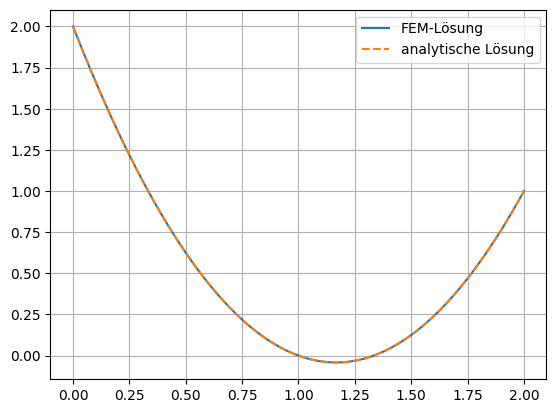
plt.plot(xi,ui, label='FEM-Lösung')
plt.plot(xi,uexact(xi),'--',label='analytische Lösung')
plt.legend(loc=1)
plt.grid()
plt.show()

Für den Fehler in der \(L_2\)-Norm folgt

Integrate((gfu-uexact(x))**2,mesh)**0.5

4.0864318637854154e-15

Der Fehler ist numerisch Null, da wir Elemente 2. Ordnung für ein Lösungpolynom 2. Ordnung benutzen.

Lösung mit zugehörigem Funktional

Wir haben im Kapitel Variationsrechnung gesehen, dass die schwache Gleichung die Nullstellengleichung der ersten Variation eines eines zugehören Funktionals sind. Es gilt daher das notwendige Kriterium

\[J(u) = \min_{v\in V} J(v)\qquad\Rightarrow\qquad \delta J(u)\,v = 0\quad \forall v\in V.\]

In NGSolve können wir einer Bilinearform die Variation eines zu definierenden Funktionals zuordnen:

Aufgabe

• Wie lautet das zugehörige Funktional \(J(u)\)?

• Berechne die zweite Variation \(\delta^2 J(u)(v\, w)\) von \(J(u)\).

u = V.TrialFunction()

# def BilinearForm
a2 = BilinearForm(V)
a2 += Variation((1/2*grad(u)*grad(u)+1/4*u**4-(-3+1/8*(4-7*x+3*x*x)**3)*u)*dx)

gfue = GridFunction(V)
gfue.Set(u0,BND)

for it in range(10):
    print ("Newton iteration", it)

    # solve linearized problem:
    # F(u_n)
    a2.Apply(gfue.vec, res)
    # F'(u_n)
    a2.AssembleLinearization(gfue.vec)
    # F'(u_n) du = F(u_n)
    du.data = a2.mat.Inverse(V.FreeDofs()) * res


    # update iteration
    # u_n+1 = u_n - du
    gfue.vec.data -= du

    #stopping criteria
    stopcritval = sqrt(abs(InnerProduct(du,res)))
    print ("<A u",it,", A u",it,">_{-1}^0.5 = ", stopcritval)
    if stopcritval < 1e-13:
        break

Newton iteration 0
<A u 0 , A u 0 >_{-1}^0.5 =  2.63044945649285
Newton iteration 1
<A u 1 , A u 1 >_{-1}^0.5 =  1.1461868091843588
Newton iteration 2
<A u 2 , A u 2 >_{-1}^0.5 =  0.23956338535903238
Newton iteration 3
<A u 3 , A u 3 >_{-1}^0.5 =  0.004330380345703788
Newton iteration 4
<A u 4 , A u 4 >_{-1}^0.5 =  6.498623278264114e-07
Newton iteration 5
<A u 5 , A u 5 >_{-1}^0.5 =  1.444693506846862e-14

gfuei = [gfue(xip) for xip in xi]

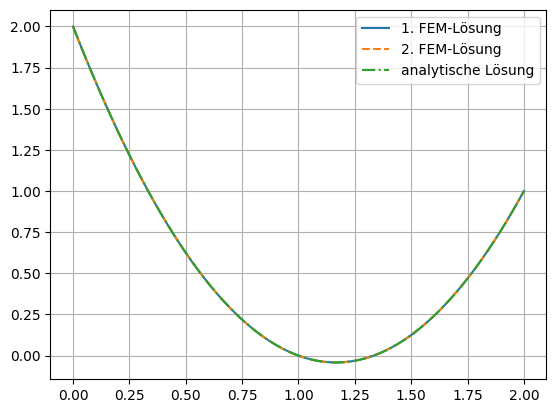
plt.plot(xi,ui,label='1. FEM-Lösung')
plt.plot(xi,gfuei,'--',label='2. FEM-Lösung')
plt.plot(xi,uexact(xi),'-.', label='analytische Lösung')
plt.legend(loc=1)
plt.grid()
plt.show()