11.3. Iterative Gleichungslöser

In Bezug auf Rechenzeit und Speicherbedarf oft viel effizientere Alternativen zur direkten Lösung von linearen Gleichungssystemen sind iterative Verfahren (insbesondere im 3D). Ausgehend von einem Startwert wird die näherungsweise Lösung iterativ verbessert. Die Verfahren benötigen nur Matrix-Vektorprodukte \(A\cdot x\).

Werden von der Matrix \(A\) nur die Nicht-Null Elemente gespeichert, so ist der Rechenaufwand für das Matrix-Vektorprodukt lediglich \(O(N)\). Als mögliches Format für dünn besetzte Matrizen (sparse matrices) sei das Compressed Sparse Row (CSR) (vgl. auch scipy sparse) erwähnt. Wir werden dieses in den Anwendungen benutzen.

In den folgenden Anwendungen unterschiedlicher iterativer Verfahren betrachten wir das Randwertproblem auf dem Einheitsquadrat

\[-\Delta u + 10\, u = 1\quad x\in\Omega = [0,1]^2\]

mit Dirichlet Randwerte \(u=0\) auf \(\partial\Omega\). Das schwache Problem lautet: gesucht ist \(u\in H_0^1(\Omega)\):

\[\int_\Omega \big(\nabla u \nabla v\, + 10\,u\, v\big) dx = \int_\Omega 1\,v\,dx\quad \forall\ v\in H_0^1(\Omega).\]

• 11.3.1. Richardson Verfahren
• 11.3.2. Jacobi und Gauss-Seidel - Verfahren
• 11.3.3. Gradienten Verfahren
• 11.3.4. CG - Verfahren

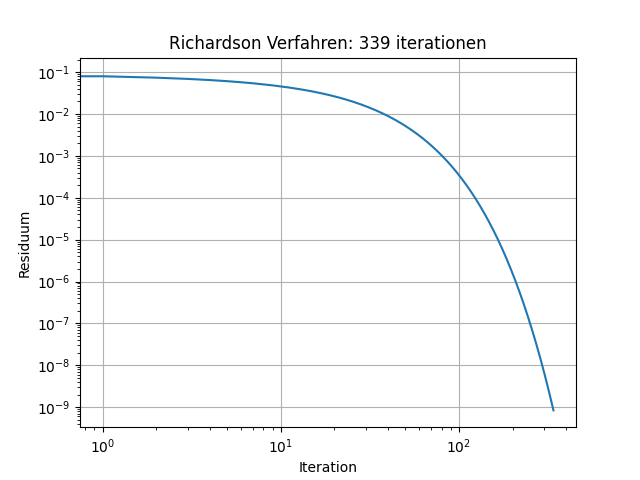
Abb. 11.2 Konvergenz Richardson Verfahrens

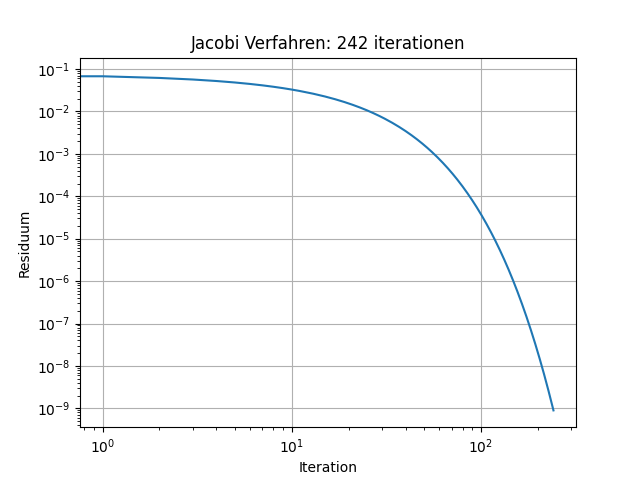
Abb. 11.3 Konvergenz Jacobi Verfahrens

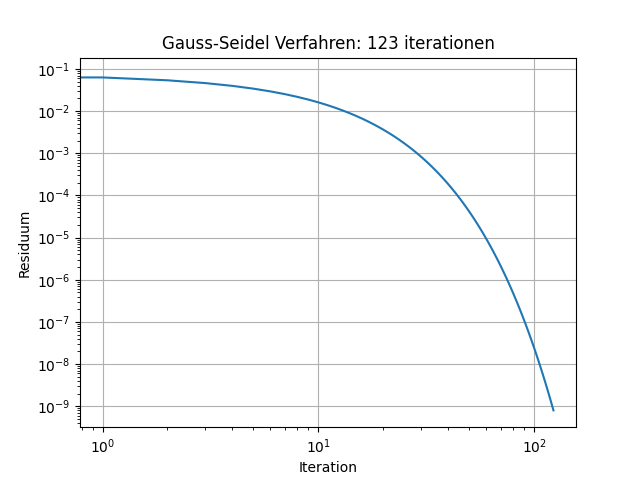
Abb. 11.4 Konvergenz Gauss-Seidel Verfahrens

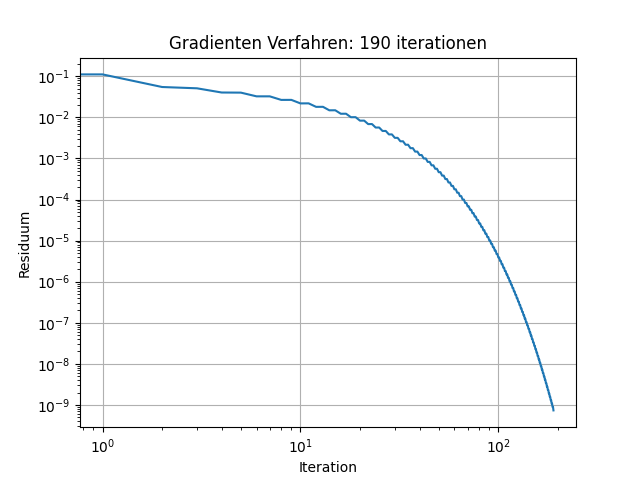
Abb. 11.5 Konvergenz Gradienten Verfahrens

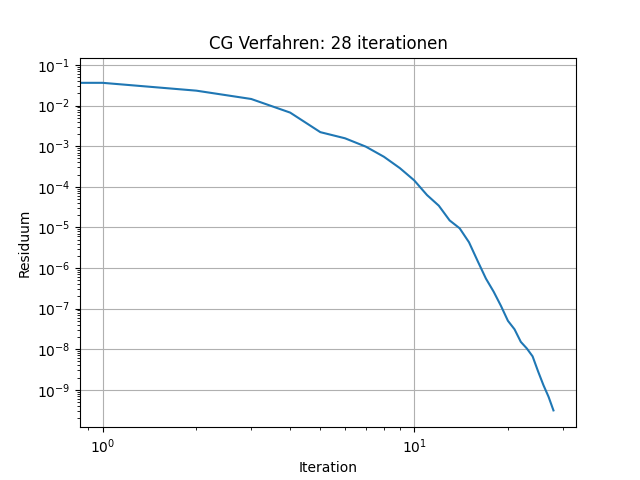
Abb. 11.6 Konvergenz CG Verfahrens