Parabolische partielle Differentialgleichungen

Inhalt

12.3. Parabolische partielle Differentialgleichungen#

Wir betrachten die parabolische Differentialgleichung

(12.5)#\[\begin{split}\begin{split}\partial_t u(t,x) - \operatorname{div}(k(x)\, \nabla u(t,x)) & = q(t,x)\quad \text{für}\ x\in \Omega\\ u(t,x) & = u_D(t,x)\quad\text{für}\ x\in \Gamma_D\\ k(x)\,\partial_n u(t,x) & = g(t,x)\quad\text{für}\ x\in \Gamma_N\\ u(0,x) & = u_0(x)\quad\text{für}\ x\in \Omega \end{split}\end{split}\]

mit den gegebenen Rand \(\partial\Omega = \Gamma_D \cup \Gamma_N\). In dem Fall muss \(\Gamma_D\not=\emptyset\) nicht gefordert werden.

Als Anwendung der parabolischen Gleichung betrachten wir den Temperaturverlauf in einem Raum (2d Querschnitt) mit einem Radiator, wobei wir für Raumseite beim Radiator eine Temperatur von 5°C als Dirichletrandwert vorgeben. Die restlichen Seiten des Raumes seien optimal isoliert, was wir mit der Neumann Randbedingung beschreiben können.

from netgen.occ import OCCGeometry, Rectangle, MoveTo, Glue, X
from ngsolve import *
from ngsolve.webgui import Draw
import numpy as np
import matplotlib.pyplot as plt

raum = Rectangle(4,2.5).Face()
raum.name = 'raum'
raum.edges.name = 'bc_raum'
raum.edges.Max(X).name = 'right'
radiator = MoveTo(3.8,0.2).Rectangle(0.1,0.8).Face()
radiator.edges.name = 'inner'
radiator.name = 'radiator'
air = raum - radiator
air.name = 'raum'
geom = Glue([air, radiator])
mesh = Mesh(OCCGeometry(geom, dim=2).GenerateMesh(maxh = 0.2))

Die schwache Gleichung für (12.5) lautet

\[\int_\Omega \partial_t u\,v\,dx + \int_\Omega k\,\nabla u\cdot\nabla v\,dx = \int_\Omega f\,v\,dx\quad \forall \ v \in H^1(\Omega).\]

In einem ersten Schritt betrachten wir die stationäre Lösung, daher die Lösung, für welche wir keine Zeitabhängigkeit (mehr) haben:

\[\int_\Omega k\,\nabla u\cdot\nabla v\,dx = \int_\Omega f\,v\,dx\quad \forall \ v \in H^1(\Omega)\]

Die Lösung unabhängig von der Zeit liegt im Sobolev-Raum \(H^1(\Omega)\).

Im zweiten Schritt suchen wir die zeitabhängige Lösung, daher die Funktion \(u: [0,T] \to H^1(\Omega)\) mit

(12.6)#\[\int_\Omega\partial_t u\,v\,dx + \int_\Omega k\,\nabla u\cdot\nabla v\,dx = \int_\Omega f\,v\,dx\quad \forall \ v \in H_0^1(\Omega),\]

wobei der Anfangswert \(u(t=0) = u_0(x)\) gegeben ist.

12.3.1. Stationäre Lösung#

Randbedingungen

mesh.GetBoundaries()

('bc_raum', 'bc_raum', 'right', 'bc_raum', 'inner', 'inner', 'inner', 'inner')

V = H1(mesh, order=3, dirichlet="right")
u = V.TrialFunction()
v = V.TestFunction()

Für den Radiator nehmen wir als Wärmequelle an:

f = LinearForm(V)
f += 100*v*dx(definedon=mesh.Materials('radiator'))
f.Assemble();

Für die Wärmeleitung haben wir abhängig vom Gebiet stückweise unterschiedliche Werte:

mesh.GetMaterials()

('raum', 'radiator')

# Luft, Wasser in der Reihenfolge der subdomains:
k = CoefficientFunction([0.0262,0.5562])

Damit können wir die Bilinearform definieren

a = BilinearForm(V)
a += k*grad(u)*grad(v)*dx
a.Assemble();

Randbedingung an der Rechten Seite des Raums ist die Front auf 5°C, die restlichen Seiten sind optimal isoliert. Ist der Radiator ausgeschaltet, sollte die Temperatur im Raum 5° konstant betragen:

gfu_D = GridFunction(V)
gfu_D.Set(CoefficientFunction(5))

gfu_stat = GridFunction(V)

Die Lösung ist gegeben durch \(u = u_0 + u_D\), wobei wir das \(u_0\) für gegebenes \(u_D\) berechnen.

gfu_stat.vec.data = gfu_D.vec
gfu_stat.vec.data += a.mat.Inverse(freedofs=V.FreeDofs())*(f.vec-a.mat*gfu_D.vec)
Draw(gfu_stat,mesh,'T stationär');

Für die stationäre Temperatur in der Mitte des Raumes erhalten wir

mip = mesh(4/2,2.5/2)
Tstat = gfu_stat(mip)
Tstat

19.212284094979978

Die mittlere Temperatur in der Luft beträgt

Aair = Integrate(1, mesh, definedon = mesh.Materials('raum'))
TstatMean = 1/Aair*Integrate(gfu_stat, mesh, definedon = mesh.Materials('raum'))
TstatMean

18.87553855924469

12.3.2. Zeitabhängige Lösung#

Mit Hilfe der stationären Gleichung erhalten wir die Temperaturverteilung nach langer (genau genommen unendlich langer) Zeit. Nun insteressiert uns der zeitliche Verlauf. Wir lösen daher das parabolische Problem.

Wir suchen also \(u(t)\), die Funktion, welche uns für jedes Zeit die örtliche Verteilung der Temperatur liefert, sprich \(u(t) \in H^1(\Omega)\).

Dazu ersetzen wir die partielle Ableitung nach der Zeit durch den Differenzenquotient:

\[\partial_t u(t) \approx \frac{u(t+\Delta t) - u(t)}{\Delta t}.\]

Es folgt für (12.6)

\[\int_\Omega \frac{u(t+\Delta t)-u(t)}{\Delta t}\,v\,dx + \int_\Omega k\,\nabla u\cdot\nabla v\,dx = \int_\Omega f\,v\,dx\quad \forall \ v \in H_0^1(\Omega).\]

Es stellt sich die Frage, für welches \(t\) wir \(\nabla u\) auswerten.

Für \(\nabla u(t)\) folgt das explizite Euler Verfahren. Durch Separation der bekannten Grössen auf die rechte Seite und der unbekannten auf die linke Seite folgt

\[\int_\Omega u(t+\Delta t)\,v\,dx = \int_\Omega u(t) v dx + \Delta t \left(\int_\Omega f(t+\Delta t)\,v\,dx - \int_\Omega k\,\nabla u(t)\cdot\nabla v\,dx\right)\quad \forall \ v \in H_0^1(\Omega)\]

In dem Fall können wir durch einfache Vektor Addition den zeitlichen Verlauf berechnen. Das Verfahren ist jedoch für grosse \(\Delta t\) nicht stabil. Wir benutzen daher diesen Ansatz nicht.
Für \(\nabla u(t+\Delta t)\) folgt das implizite Euler Verfahren

(12.7)#\[\int_\Omega (u(t+\Delta t)-u(t))\,v\,dx + \Delta t \int_\Omega k\,\nabla u(t+\Delta t)\cdot\nabla v\,dx = \Delta t \int_\Omega f\,v\,dx\quad \forall \ v \in H_0^1(\Omega).\]

Separieren wir wiederum bekanntes und unbekanntes auf die rechte bzw. linke Seite der Gleichung so folgt das Gleichungssystem

\[\int_\Omega u(t+\Delta t)\,v\,dx + \Delta t \int_\Omega k\,\nabla u(t+\Delta t)\cdot\nabla v\,dx = \int_\Omega u(t)\,v\,dx + \Delta t \int_\Omega f\,v\,dx\quad \forall \ v \in H_0^1(\Omega),\]

welches wir in jedem Zeitschritt lösen müssen. Diskret können wir das System auch als

(12.8)#\[\underbrace{(M + \Delta t\ A)}_{=:M^*}\cdot u_{n+1} = M\cdot u_n + \Delta t f\]

mit der Massenmatrix \(M\) für die Bilinearform \(\int u\,v dx\) und der Steiffigkeitsmatrix \(A\) für die Bilinearform \(\int \nabla u\cdot \nabla v\, dx\).

m = BilinearForm(V)
m += u*v*dx
m.Assemble()

<ngsolve.comp.BilinearForm at 0x10f9a54f0>

Für das \(\Delta t\) setzen wir

time = 0
dt = 1

Damit folgt für \(M^*\)

mstar = m.mat.CreateMatrix()
mstar.AsVector().data = m.mat.AsVector() + dt * a.mat.AsVector()
invmstar = mstar.Inverse(freedofs=V.FreeDofs())

Der Anfangswert ist gegeben durch

gfu = GridFunction(V)
gfu.vec.data = gfu_D.vec

scene = Draw(gfu,mesh,"u");

res = gfu.vec.CreateVector()
tstep = 600 # time that we want to step over within one block-run

\(M^*\cdot(u_{0,n+1}+u_D) = M\cdot u_n + \Delta t\, f\)

t_intermediate=0 # time counter within one block-run
while t_intermediate < tstep - 0.5 * dt:
    res.data = m.mat*gfu.vec + dt * f.vec - mstar*gfu_D.vec
    gfu.vec.data = gfu_D.vec
    gfu.vec.data += invmstar * res 
    t_intermediate += dt
    scene.Redraw()
time+=t_intermediate

Oft benutzt man auch eine inkrementelle Berechnung. Mit \(\delta u = u(t+\Delta t)-u(t)\) folgt für (12.7)

\[\int_\Omega \delta u\,v\,dx + \Delta t \int_\Omega k\,\nabla \delta u\cdot\nabla v\,dx + \Delta t \int_\Omega k\,\nabla u(t)\cdot\nabla v\,dx = \Delta t \int_\Omega f\,v\,dx\quad \forall \ v \in H_0^1(\Omega).\]

und damit

\[\int_\Omega \delta u\,v\,dx + \Delta t \int_\Omega k\,\nabla \delta u\cdot\nabla v\,dx = \Delta t \int_\Omega f\,v\,dx - \Delta t \int_\Omega k\,\nabla u(t)\cdot\nabla v\,dx\quad \forall \ v \in H_0^1(\Omega).\]

Für das diskrete System folgt

\[\underbrace{(M + \Delta t\ A)}_{=:M^*}\cdot \delta u_{n+1} = \Delta t\, f - \Delta t\, A\cdot u_n.\]

Die Form hat den entscheidenden Vorteil, dass die Dirichletrandwerte nicht in jedem Zeitschritt berechnet werden müssen. Wir sparen uns daher eine Matrix Multiplikation und Vektor Initialisierung.

time = 0
gfu2 = GridFunction(V)
gfu2.vec.data = gfu_D.vec

scene2 = Draw(gfu2,mesh,'u');

t_intermediate=0 # time counter within one block-run
# Temperatur in Raummitte
T = [gfu2(mip)]
Tmean = [1/Aair*Integrate(gfu2, mesh, definedon = mesh.Materials('raum'))]
while t_intermediate < tstep - 0.5 * dt:
    res.data = dt * f.vec - dt * a.mat * gfu2.vec
    gfu2.vec.data += invmstar * res
    t_intermediate += dt
    T.append(gfu2(mip))
    Tmean.append(1/Aair*Integrate(gfu2, mesh, definedon = mesh.Materials('raum')))
    scene2.Redraw()
time+=t_intermediate

Draw(gfu-gfu_stat,mesh,'Differenz');

12.3.3. Erweiterung mit Konvektion#

Wir erweitern das parabolische Problem noch durch einen konvektiven Term. Daher eine Strömung, welche die Temperatur im Raum verteilt.

\[\begin{split}\begin{split}\partial_t u(t,x) - \operatorname{div}(k(x)\, \nabla u(t,x)) + b\cdot \nabla u & = q(t,x)\quad \text{für}\ x\in \Omega\\ u(t,x) & = u_D\quad\text{für}\ x\in \partial\Omega \end{split}\end{split}\]

Das Strömungsfeld \(b\) nennt man wind, wir definieren dieses gegeben als

\[\begin{split}b(x,y) = v_0 \begin{pmatrix} -\frac{(y-1.25)}{1.25}\, \left(1-\left(\frac{x}{4}\right)\,\frac{x}{4}\right)\\ \frac{(x-2)}{2} \frac{y}{2.5}\,\left(1-\left(\frac{y}{2.5}\right)\right)\end{pmatrix}\end{split}\]

v0 = 2
b = v0*CoefficientFunction((-(y-1.25)/1.25*(1-(x/4))*x/4, (x-2)/2*y/2.5*(1-y/2.5)))
Draw(b,mesh,"wind");
from ngsolve.internal import visoptions
visoptions.scalfunction = "wind:0"

a = BilinearForm(V, symmetric=False)
a += k*grad(u)*grad(v)*dx + b*grad(u)*v*dx
a.Assemble();

Für die stationäre Lösung folgt

gfu_stat2 = GridFunction(V)
gfu_stat2.vec.data = gfu_D.vec
gfu_stat2.vec.data += a.mat.Inverse(freedofs=V.FreeDofs())*(f.vec - a.mat*gfu_D.vec)

Wie beobachtet werden kann ist die Lösung unphysikalisch. Wird \(v_0\) zu gross gewählt, wird das numerische Problem instabil. In dem Fall müssen wir entweder

die Diskretisierung stabilisieren
oder das Mesh feiner wählen.

Draw(gfu_stat2,mesh,'u2 stationär');

Tstat2 = gfu_stat2(mip)
print('stationäre Temperatur in Raum Mitte: ', Tstat2)

Tstat2Mean = 1/Aair*Integrate(gfu_stat2, mesh, definedon = mesh.Materials('raum'))
print('stationäre mittlere Temperatur: ', Tstat2)

stationäre Temperatur in Raum Mitte:  17.38781592415372
stationäre mittlere Temperatur:  17.38781592415372

mstar = m.mat.CreateMatrix()
mstar.AsVector().data = m.mat.AsVector() + dt * a.mat.AsVector()
invmstar = mstar.Inverse(freedofs=V.FreeDofs())

gfu3 = GridFunction(V)

time = 0
gfu3.vec.data = gfu_D.vec

scene3 = Draw(gfu3,mesh,'u');

t_intermediate=0 # time counter within one block-run
# Temperatur in Raummitte
Tkonv = [gfu3(mip)]
TkonvMean = [1/Aair*Integrate(gfu3, mesh, definedon = mesh.Materials('raum'))]
while t_intermediate < tstep - 0.5 * dt:
    res.data = dt * f.vec - dt * a.mat * gfu3.vec
    gfu3.vec.data += invmstar * res
    t_intermediate += dt
    Tkonv.append(gfu3(mip))
    TkonvMean.append(1/Aair*Integrate(gfu3, mesh, definedon = mesh.Materials('raum')))
    scene3.Redraw()
time+=t_intermediate

Im Bereich vor dem Radiator ist es bedeutend kühler, hingegen durch den Abtransport der Wärme oberhalb bedeutend wärmer.

Draw(gfu3-gfu2,mesh,'Differenz');

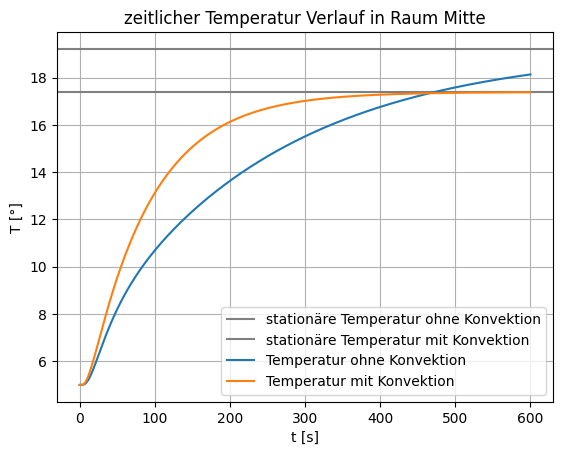
Für die zeitliche Entwicklung der Tempertur der beiden Ansätze erhalten den folgenden Verlauf

../_images/396345b9e2d72661e0786d712ff357a72561132a43cfe7a00f1b901dbc4915a8.png

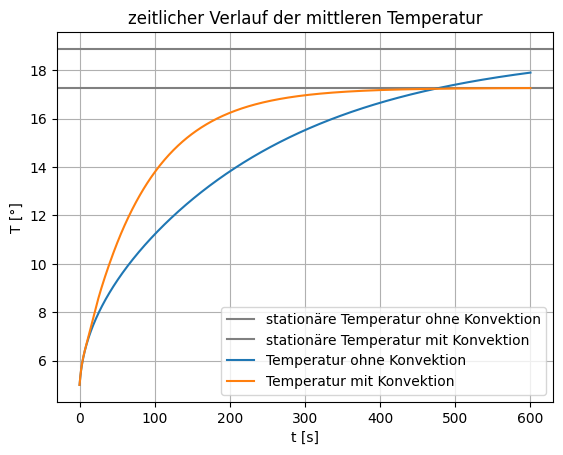
../_images/a3f6064a31cc53bd832a2853b1e729e6bf0907727985cbe3cf9fdcdf89e8bc1e.png