Einstiegsbeispiel: Espresso in Isolations- und Keramiktasse

Inhalt

1.2. Einstiegsbeispiel: Espresso in Isolations- und Keramiktasse#

1.2.1. Problemstellung#

Zur praktischen Illustration der Poisson-Gleichung betrachten wir die Wärmeleitung. In der Anwendung wollen wir den Unterschied zwischen einer doppelwandigen Esspressotasse und einer normalen illustrieren. Dabei betrachten wir die Temperaturverteilung im Raum, wobei die Wärmeleitung vom Ort abhängig ist. Damit können unterschiedliche Objekte wie die Luft, Isolation, das Glas und der Kaffee beschrieben bzw. modelliert werden.

Das Gebiet \(\Omega\) kann im zwei- oder dreidimensionalen Raum liegen.

../_images/Kaffeetassen.jpeg — Abb. 1.1 Unterschiedliche Espressotassen#

Die Wärmeleitung wird in der Physik als Diffusionsprozess beschrieben. Mathematisch kann man solche Prozesse mit Hilfe der Poisson-Gleichung modellieren. Wir betrachten daher ein skalares Temperaturfeld \(T: \Omega \to \mathbb{R}\) welches dem Randwertproblem

(1.7)#\[\begin{split}\begin{split}-\mathop{div}(\lambda(x) \nabla T(x)) & = q(x)\quad\text{für}\ x\in\Omega\\ T(x) & = T_0(x)\quad\text{für}\ x\in\Gamma_D\end{split}\end{split}\]

genügt, wobei \(\lambda=\lambda(x)\) der ortsabhängige Wärmeleitungskoeffizient ist. Der zugehörige Wärmefluss

(1.8)#\[q = -\lambda \nabla T\]

ist gegeben durch den Gradient der Temperatur \(\nabla T\). Im Fall, dass \(\lambda\) diskontinuierlich ist, wird die Gleichung im Sinne von Distributionen verstanden. Dies beinhaltet Interface Bedingungen: Die Temperatur auf der linken und rechten Seite sind gleich und der Wärmefluss der linken in die rechte Seite müssen gleich gross sein:

\[\begin{split}\begin{split} T_l & = T_r \\ \lambda_l \frac{\partial T_r}{\partial n} & = \lambda_r \frac{\partial T_r}{\partial n} \end{split}\end{split}\]

Für \(T_0 = 0\) ist die variationelle Form des Problems gegeben durch: finde \(T \in H_0^1(\Omega)\) mit

\[ \int_\Omega \lambda(x) \nabla T\cdot \nabla v dx = \int_\Omega q\, v dx \]

Diskontinuierliche Koeffizienten bilden kein Problem. Beide Interface Bedingungen werden erfüllt:

Stetigkeit der Temperatur \(T\) durch die Stetigkeit der Ansatzfunktionenraumes
Stetigkeit des Wärmeflusses in einem schwachen Sinne, durch Neumann Randbedingungen.

1.2.2. Geometrie und Mesh#

Als erstes definieren wir die Geometrie der Tasse, Flüssigkeit und Umgebung mit Hilfe des Open Cascade Technology (OCCT) Geometry Kernels.

wp = WorkPlane()
sPnts = [(0.024, 0.008),
         (0.028, 0.016),
         (0.032, 0.04),
         (0.022, 0.02),
         (0.004, 0.006),
         (-0.004, 0.006),
         (-0.022, 0.02),
         (-0.032, 0.04),
         (-0.028, 0.016),
         (-0.024, 0.008),
         (-0.016, 0)]
wp.MoveTo(4*4e-3,0).Spline(sPnts)
face = wp.Close().Face()

Das Innere ist durch die Orientierung des Randes gegeben. Setzen wir uns auf den Rand, so ist auf der linken Seite das Innere und auf der rechten das Äussere. Daher ist hier die Geometrie in positiver mathematischer Orientierung definiert.

p = np.array(sPnts)
plt.plot(p[:,0],p[:,1],'o-.')
for i,pi in enumerate(p):
    plt.text(*(np.array(pi)+np.array([0.001,0])),str(i))
plt.show()

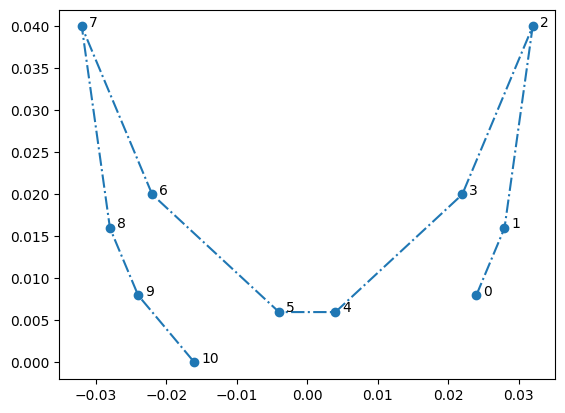
../_images/80ab112e94c27a53a29ce6e57c60ad8ab75d9be4176f60c3c11104a2e4c1a552.png

Damit erhalten wir die Tasse ohne Vakuum Bereich:

DrawShape(face);

Den inneren Vakuum Bereich definieren wir analog:

wp2 = WorkPlane()
sPnts2 = [(0.0224, 0.008),
          (0.0264, 0.016),
          (0.0312, 0.036),
          (0.022, 0.0184),
          (0.004, 0.0048),
          (-0.004, 0.0048),
          (-0.022, 0.0184),
          (-0.0312, 0.036),
          (-0.0264, 0.016),
          (-0.0224, 0.008),
          (-0.0152, 0.0012)]
wp2.MoveTo(4*3.8e-3,4*.3e-3).Spline(sPnts2)
isolator = wp2.Close().Face()

DrawShape(isolator);

Das Glas ist daher gegeben durch die Boolsche Operaton face - isolator:

glas = face-isolator

DrawShape(glas);

Die Flüssigkeit wird ähnlich aufgebaut. Wir definieren ein Trapez und subtrahieren die Fläche der Tasse:

wp3 = WorkPlane()
wp3.MoveTo(-4*3.9e-3,2*1.5e-3).LineTo(4*3.9e-3,2*1.5e-3).LineTo(4*7.2e-3,3*9.5e-3).LineTo(-4*7.2e-3,3*9.5e-3)
face3 = wp3.Close().Face()
liquid = face3-face

DrawShape(liquid);

Und letztlich noch für die Luft analog:

wp4 = WorkPlane()
wp4.MoveTo(-.2,0).LineTo(.2,0).LineTo(.2,.25).LineTo(-.2,.25)
box = wp4.Close().Face()
air = box-face-face3

DrawShape(air);

Alles zusammen geklebt glue liefert unser Modell. Um später die einzelnen Teilflächen / Gebiete mit verschiedenen Materialparameter versehen zu können definieren wir Namen. Ebenso können wir Ränder bezeichnen und die Feinheit des Meshes beeinflussen:

air.faces.name = 'air'
glas.faces.name = 'glas'
isolator.faces.name = 'isolator'
liquid.faces.name = 'liquid'

air.maxh = 30e-3
isolator.maxh = 5e-3
glas.maxh = 5e-4
liquid.maxh = 2.5e-3

glas.edges.Min(Y).name='bottom'
air.edges.Min(X).name='outer'
air.edges.Max(X).name='outer'
air.edges.Max(Z).name='outer'
air.edges.Max(Y).name='outer'
air.edges.Nearest((-.1,0)).name='bottom'
air.edges.Nearest((.1,0)).name='bottom'

model = Glue([air, glas, isolator, liquid])

DrawShape(model);

Abschliessend benutzen wir das Modell für die OCC-Geometrie und generieren das netgen Mesh, welches wir wiederum ngsolve übergeben:

geo = OCCGeometry(model, dim=2) # wichtig: dim=2 muss hier zwingend definiert werden!
mesh = Mesh(geo.GenerateMesh())

Draw(mesh);

Das geometrische Modell und dessen mathematische Beschreibung als Mesh ist damit definiert.

1.2.3. Stationäre Wärmeleitung#

Ortsabhängige Wärmeleitung#

Die stationäre Wärmeverteilung kann wie oben erwähnt mit Hilfe der Poisson-Gleichung modelliert werden. Es wird dabei vorausgesetzt, dass die Wärme sich diffusiv im Raum verteilt. In dem Ansatz wird keine Wärmestrahlung oder Konvektion berücksichtigt. Wir gehen davon aus, dass es keine Luftströmung aufgrund von Temperaturdifferenzen in der Luft gibt, welche die Wärme weg transportieren würde. Wie gut die Wärme geleitet wird, hängt vom Medium ab. Wir benutzen folgende Werte für die Wärmeleitung:

Fall Isolationstasse: wir gehen von Luft als relativ schlechter Wärmeleiter im Innern der Tasse aus.

lam_mat = {'glas': 20, 'isolator': 0.0262, 'liquid': 0.597, 'air': 0.0262}
lam = CoefficientFunction([lam_mat[mat] for mat in mesh.GetMaterials()])

Fall Keramiktasse: kein Isolator, wir setzen die Wärmeleitung auf Glas (für Keramik).

lam_mat2 = {'glas': 20, 'isolator': 20, 'liquid': 0.597, 'air': 0.0262}
lam2 = CoefficientFunction([lam_mat2[mat] for mat in mesh.GetMaterials()])

Durch Testen der partiellen Differentialgleichung (1.7) erhalten wir wie in (1.3) die schwache Gleichung

(1.9)#\[\int_\Omega \lambda(x) \nabla T(x)\cdot\nabla v(x) dx = \int_\Omega q(x) v(x) dx\quad \forall \ v\in\ H_0^1(\Omega),\]

wobei wir die Randbedingung in dem Fall homogen auf \(T_0 \equiv 0\) gesetzt haben. Wir betrachten daher die relative Temperaturänderung zur Umgebungstemperatur \(T_0\).

Die Lösung des Randwertproblems (1.7) suchen wir in einem geeigneten Funktionenraum (in dem Fall der \(H_0^1(\Omega)\), welchen wir später einführen werden). Der Funktionenraum ist unendlichdimensional, was numerisch nicht zielführend ist. Mit Hilfe von finiter Elemente Basisfunktionen führen wir eine Basis ein, welche den Funktionenraum approximiert und endlichdimensional ist.

order = 3
V = H1(mesh,order = order, dirichlet = 'bottom')
u = V.TrialFunction()
v = V.TestFunction()

Damit haben wir das unendlichdimensionale Problem auf ein endlich dimensionales reduziert.

print('V.ndof = ',V.ndof)

V.ndof =  4801

Wir betrachten nun die beiden verschiedenen Tassen, was zu unterschiedlichen Bilinearformen oder diskret in dem Fall Matrizen \(A\) führt:

# Isolationstasse
a = BilinearForm(V,symmetric=True)
a += lam*grad(u)*grad(v)*dx
a.Assemble();

# Keramiktasse
a2 = BilinearForm(V,symmetric=True)
a2 += lam2*grad(u)*grad(v)*dx
a2.Assemble();

Kaffee als Wärmequelle#

Als nächstes müssen wir den Wärmeeintrag modellieren. Hier können unterschiedliche Ansätze verfolgt werden. Wir betrachten als ersten den einfachsten Ansatz und betrachten den warmen Kaffee als Wärmequelle \(q(x)\). Die Wärmequelle geht in die rechten Seite der Gleichung (1.9). Die rechte Seite hängt nur von den Testfunktionen ab und führt daher zu einer Linearform. Im endlichdimensionalen entsprechend auf einen Vektor \(b\):

f = LinearForm(V)
f += CoefficientFunction(6e4)*v*dx('liquid')
f.Assemble()

<ngsolve.comp.LinearForm at 0x1062824b0>

Damit haben wir letztlich ein lineares Gleichungssystem

\[A \cdot T = b\]

zu lösen. Für die numerischen Lösungen gibt es in ngsolve sogenannte GridFunction’s.

gfT = GridFunction(V)
gfT2 = GridFunction(V)

gfT.vec.data += a.mat.Inverse(freedofs=V.FreeDofs())*f.vec
gfT2.vec.data += a2.mat.Inverse(freedofs=V.FreeDofs())*f.vec

Die beiden Lösungen illustrieren sehr schön den Unterschied zwischen diesen beiden Tassen. Die Temperatur in der Isolationstasse ist viel höher als in der Keramiktasse. Dieses Resultat lehrt uns auch die Erfahrung, dass in der Isdolationstasse der Kaffee bedeutend länger warm ist, als in der Keramiktasse.

Temperaturverteilung für die Isolationstasse

Draw(gfT,min=0,max=60);

Temperaturverteilung für die Keramiktasse

Draw(gfT2,min=0,max=60);

Wir können auch den Wärmefluss visualisieren und erhalten mit (1.8):

Wärmefluss für die Isolationstasse

q = -lam*grad(gfT)
Draw(q,mesh,'q');

Wärmefluss für die Keramiktasse

q2 = -lam2*grad(gfT2)
Draw(q2,mesh,'q2');

Durch aktivieren der Vektoren in der Visualisierung kann man sehr schön den Unterschied sehen. Im Fall der Isolationstasse wird der direkte Wärmefluss zum unteren Rand unterdrückt, was eine viel bessere Isolation bewirkt und damit natürlich auch einen warmen Kaffee garantiert.

Wir werden dieses Beispiel später im Semester wieder aufgreifen und noch näher an der Realität ansetzen und insbesondere zeitabhängig betrachten. In dieser alltäglich praktischen Anwendung sehen Sie das Potential des Moduls. Während dem Semester werden wir die benutzten Begriffe einführungen und letztlich in der Lage sein, praktische Anwendungen modellieren und rechnen zu können.