3.2. Metrische Räume

3.2.1. Metrik

In der Analysis will man oft eine Distanz zwischen zwei Elemente eines Vektorraumes angeben. Insbesondere bei Konvergenzbetrachtungen ist der Abstand zweier Elemente existentiell wichtig. Der Konvergenzbegriff in \(\mathbb{R}\) unter Hinzunahme der folgenden Distanzfunktion

\[\begin{split}\begin{split} d : \mathbb{R}\times\mathbb{R} & \to \mathbb{R}^+\\ (x,y) & \mapsto d = d(x,y) := |x-y|\end{split}\end{split}\]

lautet wie folgt: Die Folge \(\{x_n\}\) aus \(\mathbb{R}\) heisst konvergent gegen \(x_0\in\mathbb{R}\), wenn es zu jedem \(\varepsilon > 0\) eine natürliche Zahl \(n_0 = n_0(\varepsilon)\) gibt, so dass

\[d(x_n,x_0) = |x_n-x_0| < \varepsilon\]

für alle \(n \ge n_0\) gilt.

Definition 3.5 (Metrik)

Eine nichtleere Menge \(V\) mit Elemente \(x, y, z, \ldots\) heisst ein metrischer Raum, wenn jedem Paar \(x, y \in V\) eine reelle Zahl \(d(x,y)\), genannt Abstand oder Metrik, zugeordnet ist, mit den Eigenschaften: Für alle \(x,y,z\in V\) gilt

1. \(d(x,y) \ge 0,\ d(x,y) = 0\) genau dann, wenn \(x=y\) ist

2. \(d(x,y) = d(y,x)\) Symmetrieeigenschaft

3. \(d(x,y) \le d(x,z) + d(z,y)\) Dreiecksungleichung.

Für metrische Räume verwenden wir wieder die Schreibweisen: \((V, d)\) oder kurz \(V\), falls der Kontext klar ist.

Aufgabe

Zeige, dass für \(V = C[0,1]\), den stetigen Funktionen auf dem Intervall \([0,1]\) die Abbildung

(3.1)\[\begin{split}\begin{split}d_{\text{max}} : V \times V & \to \mathbb{R}^+\\ (x,y) & \mapsto d_{\text{max}}(x,y) := \max_{t\in[0,1]} |x(t)-y(t)|\end{split}\end{split}\]

eine Metrik definiert (Maximumsmetrik).

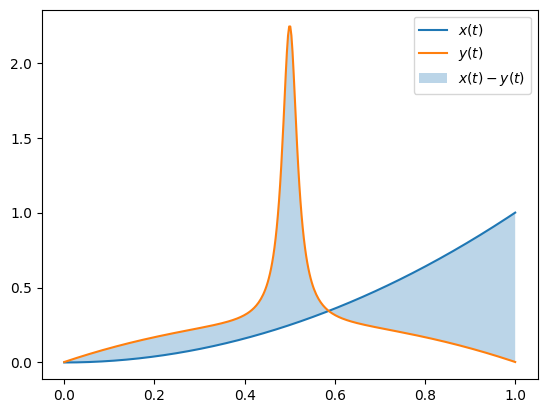
Beispiel: Betrachte \(x(t), y(t)\) gegeben durch

\[\begin{split}\begin{split} x(t) & = t^2\\ y(t) & = t\,(1-t) + \frac{2}{1+\left(50\,\big(t-\frac{1}{2}\big)\right)^2}. \end{split}\end{split}\]

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

x = lambda t: t**2
y = lambda t: t*(1-t)+2/(1+((t-0.5)/0.02)**2)

t = np.linspace(0,1,400)

plt.plot(t,x(t), label='$x(t)$')
plt.plot(t,y(t), label='$y(t)$')
plt.legend()
plt.show()

Die Maximummetrik berechnet die maximale Differenz der beiden Funktionen:

Show code cell source Hide code cell source

plt.plot(t,np.abs(x(t)-y(t)), label='$|x(t)-y(t)|$')
plt.legend()
plt.show()

Aufgabe

Berechne analytisch den exakten Wert der Maximumsmetrik für die beiden Funktionen \(x,y\) aus obigem Beispiel.

Eine weitere wichtige Metrik ist die Integralmetrik. Es sei \(V\) die Menge aller reellwertigen Funktionen, die auf einem (nicht notwendig beschränkten) Intervall \((a,b)\) stetig sind und für die das Integral

\[\int_a^b |x(t)|^p dt, \quad 1\le p < \infty\]

im Riemannschen Sinne existiert. Setzen wir für \(x(t), y(t)\in V\)

Definition 3.6 (Integralmetrik)

\[d_p(x,y) := \left(\int_a^b |x(t)-y(t)|^p dt\right)^{1/p},\quad 1\le p < \infty\]

so wird \(V\) mit dieser Integralmetrik zu einem metrischen Raum. Der Beweis nutzt die Minkowski-Ungleichung für Integrale

\[\left(\int_a^b |u(t)+v(t)|^p dt\right)^{1/p} \le \left(\int_a^b |u(t)|^p dt\right)^{1/p} + \left(\int_a^b |v(t)|^p dt\right)^{1/p}.\]

Beispiel:

Show code cell source Hide code cell source

plt.plot(t,x(t), label='$x(t)$')
plt.plot(t,y(t), label='$y(t)$')
plt.fill_between(t,x(t),y(t),alpha=0.3, label='$x(t)-y(t)$')
plt.legend()
plt.show()

Aufgabe

Berechne die Integralmetrik für \(p=2\) für das Beispiel oben.

Aufgabe

In der Codierungstheorie ist ein \(n\)-stelliges Binärwort ein \(n\)-Tuppel \((\xi_1, \ldots, \xi_n)\), wobei \(\xi_k \in \{0,1\}\) für \(k=1,\ldots, n\). Bezeichne \(V\) die Menge aller dieser Binärwörter. Für \(x = \xi_1 \xi_2 \ldots \xi_n\), \(y = \eta_1 \eta_2 \ldots \eta_n\) ist die Hamming-Distanz zwischen \(x\) und \(y\) durch

\[d_H(x,y) := \text{Anzahl der Stellen an denen sich $x$ und $y$ unterscheiden}\]

definiert. Zeige:

1. \(d_H(x,y)\) lässt sich durch

   \[d_H(x,y) := \sum_{k=1}^n [(\xi_k+\eta_k) \mod 2]\]

   darstellen.

2. \((V,d_H)\) ist ein metrischer Raum.

Die topologischen Begriffe wie offene Kugel, innerer Punkt, Häufungspunkt, abgeschlossen, beschränkt lassen sich mit Hilfe der Metrix \(d\) für einen metrischen Raum \((V,d)\) direkt aus dem aus der Analysis bekannten \(\mathbb{R}^n\) übertragen.

Definition 3.7 (Konvergenz)

Eine Folge \(\{x_n\}\subset V\) von Elemente aus \(V\) heisst konvergent, wenn es ein \(x_0\in V\) gibt mit

\[d(x_n,x_0) \to 0\quad \text{für}\quad n\to\infty,\]

dh. wenn es zu jedem \(\varepsilon > 0\) ein \(n_0 = n(\varepsilon)\in\mathbb{N}\) gibt, mit

\[d(x_n,x_0) < \varepsilon\quad\text{für alle}\quad n\ge n_0.\]

Schreibweise: \(x_n \to x_0\) für \(n \to \infty\) oder \(\lim_{n\to\infty} x_n = x_0\), \(x_0\) heisst Grenzwert der Folge \(\{x_n\}\)

Der Grenzwert einer konvergenten Folge ist eindeutig bestimmt. Dies lässt sich per Widerspruch wie folgt leicht zeigen. Seien \(x_0\) und \(y_0\) zwei verschiedene Grenzwerte. Daher gilt

\[\begin{split}\begin{split} 0 < d(x_0,y_0) & \le d(x_0, x_n) + d(x_n,y_0)\\ & = \underbrace{d(x_n,x_0)}_{\to 0\ \text{für}\, n\to 0} + \underbrace{d(x_n,y_0)}_{\to 0\ \text{für}\, n\to 0} \to 0\ \text{für}\, n\to 0.\end{split}\end{split}\]

Es folgt damit \(d(x_0,y_0)=0\) und damit \(x_0 = y_0\).

3.2.2. Funktionenfolgen

Wir starten mit einem intuitiven Begriff der Konvergenz für Funktionenfolgen:

Definition 3.8 (Punktweise Konvergenz)

Man nennt eine Funktionenfolge \(\{x_n(t)\} \subset C[a,b]\) punktweise konvergent, wenn für jedes \(t\in [a,b]\) die Zahlenfolge \(x_1(t), x_2(t), \ldots \) konvergiert. Die Grenzfunktion \(x\) ist dabei durch

\[\lim_{n\to\infty} x_n(t) = x(t)\quad\text{für jedes}\quad t\in [a,b]\]

gegeben.

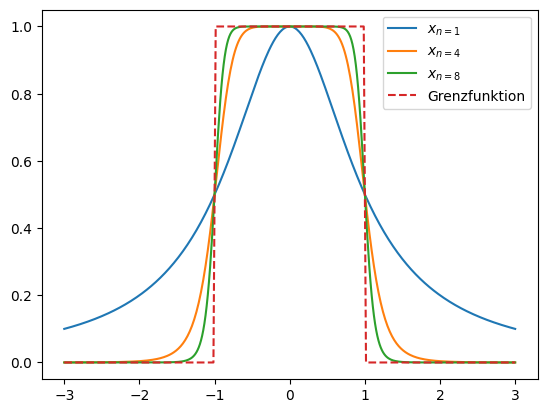
Die punktweise Konvergenz erweist sich für die Analysis als zu schwach. Als Beispiel dazu betrachten wir die Folge der Funktionen \(x_n \subset C(\mathbb{R})\)

\[x_n(t) = \frac{1}{1+t^{2n}},\quad n=1,2,3,\ldots\]

Wie im Python Code unten leicht zu sehen ist, konvergiert die Folge punktweise gegen

\[\begin{split}x(t) = \begin{cases} 1,\quad \text{für}\ |t| < 1,\\ 1/2, \quad \text{für}\ |t| = 1,\\ 0, \quad \text{für}\ |t| > 1.\end{cases}\end{split}\]

Obwohl alle Funktionen \(x_n\) stetig sind, ist die Grenzfunktion \(x\) unstetig und damit nicht in unserem Funktionenraum (oder Vektorraum) \(x\not\in C(\mathbb{R})\)! Das ist für uns unbrauchbar.

Show code cell source Hide code cell source

def x(t):
    y = np.zeros_like(t)
    y[np.abs(t)<1] = 1
    y[np.abs(t)==1] = 0.5
    return y

xn = lambda t,n : 1/(1+t**(2*n))
t = np.linspace(-3,3,400)

plt.plot(t,xn(t,1), label=r'$x_{n=1}$')
plt.plot(t,xn(t,4), label=r'$x_{n=4}$')
plt.plot(t,xn(t,8), label=r'$x_{n=8}$')
plt.plot(t,x(t),'--', label='Grenzfunktion')
plt.legend()
plt.show()

Das Problem der punktweisen Konvergenz besteht darin, dass für jedes \(t\in\mathbb{R}\) eine eigene Schranke \(\varepsilon = \varepsilon(t)\) gewählt werden kann. Dies ist zu schwach, um garantieren zu können, dass eine konvergente Funktionenfolge wieder stetig ist. Wir benutzen nun die Maximumsmetrik (3.1). Daraus folgt, dass zu jedem \(\varepsilon > 0\) es ein \(n_0 = n_0(\varepsilon) \in \mathbb{N}\) mit

\[\max_{t\in\mathbb{R}} |x_n(t) - x(t)| < \varepsilon\quad \text{für alle}\ n \ge n_0\]

geben muss. Zu jedem \(\varepsilon > 0\) ist hier im Sinne von „beliebig klein“ zu verstehen. Der grosse Unterschied zur punktweisen Konvergenz ist, dass hier das \(\varepsilon\) für alle \(t\in\mathbb{R}\) das selbe ist. In diesem Sinne ist jedoch die Funktionenfolge \(x_n\) nicht mehr konvergent:

Show code cell source Hide code cell source

epsilon = 0.1

plt.plot(t,xn(t,1), label=r'$x_{n=1}$')
plt.plot(t,xn(t,4), label=r'$x_{n=4}$')
plt.plot(t,xn(t,8), label=r'$x_{n=8}$')
plt.plot(t,x(t),'--', label='Grenzfunktion')
plt.fill_between(t,x(t)-epsilon,x(t)+epsilon,label=r'$\varepsilon$-Schranke',alpha=0.3)
plt.legend()
plt.show()

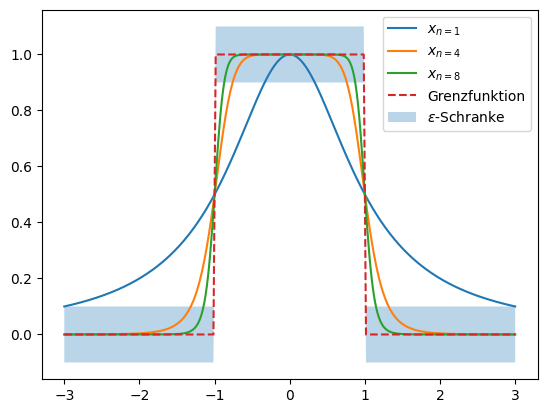
Für ein \(\varepsilon < 1\) (Sprunghöhe) finden wir kein \(n_0\) so, dass der Abstand zur Grenzfunktion der Bedingung genügt. Die Funktionenfolge ist daher nicht konvergent bezüglich der Maximumsmetrik.

Definition 3.9 (Gleichmässige Konvergenz)

Die Konvergenz in \((C[a,b],d_{\max})\) nennt man gleichmässige Konvergenz auf dem Intervall \([a,b]\).

Bemerkung

Ist eine stetige Funktionenfolge gleichmässig konvergent, so ist die Grenzfunktion wiederum stetig.

3.2.3. Cauchy-Folge

Der Begriff der Cauchy-Folge folge kann direkt auf metrische Räume übertragen werden:

Definition 3.10 (Cauchy-Folge)

Eine Folge \(\{x_n\}\) aus dem metrischen Raum \(V\) heisst Cauchy-Folge, wenn

\[\lim_{m,n\to\infty} d(x_n,x_m) = 0\]

ist, dh. wenn es zu jedem \(\varepsilon > 0\) eine natürliche Zahl \(n_0 = n_0(\varepsilon)\in\mathbb{N}\) git mit

\[d(x_n,x_m) < \varepsilon\quad\text{für alle}\quad n,m \ge n_0.\]

Theorem 3.1

Jede konvergente Folge im metrischen Raum \(V\) ist auch eine Cauchy-Folge.

Proof. Aus der Konvergenz der Folge \(\{x_n\}\) folgt: Zu jedem \(\varepsilon>0\) gibt es ein \(n_0 = n_0(\varepsilon)\in\mathbb{N}\) und ein \(x_0\in V\) mit

\[d(x_n,x_0) < \varepsilon\quad\text{und}\quad d(x_m,x_0) < \varepsilon\]

für alle \(n,m \ge n_0\). Mit Hilfe der Dreiecksungleichung folgt

\[d(x_n,x_m) \le d(x_n,x_0) + d(x_0,x_m) = d(x_n,x_0) + d(x_m,x_0) < 2 \varepsilon\]

für alle \(n,m \ge n_0\).

Die Umkehrung gilt im allgemeinen nicht.

Beispiel: Betrachte \(V = (0,1)\) mit der Metrik \(d(x,y) := |x-y|\) und der Folge \(\{x_n\}\) mit \(x_n = \frac{1}{1+n}\). Die Folge ist eine Cauchy-Folge im metrischen Raum \((V,d)\), besitzt jedoch keinen Grenzwert in diesem \((0\not\in V)\).

Das führt uns zu einem neuen Begriff, der Vollständigkeit. Wir interessieren uns insbesondere für diejenigen metrischen Räume, in denen Cauchy-Folgen konvergieren.

Definition 3.11 (Vollständig)

Ein metrischer Raum \(V\) heisst vollständig, wenn jede Cauchy-Folge in \(V\) gegen ein Element von \(V\) konvergiert.

Betrachten wir ein paar Beispiele:

1. \(\mathbb{R}^n\) mit der euklidischen Metrik

   \[d(x,y) = \sqrt{\sum_{k=1}^n |x_k-y_k|^2}\]

   versehen, ist ein vollständiger metrischer Raum. Dies folgt aus dem Cauchyschen Konvergenzkriterium für Punktfolgen.

2. \(C[a,b]\) mit der Maximumsmetrik

   \[d(x,y) = \max_{a\le t\le b} |x(t)-y(t)|\]

   versehen ist vollständig.

Remark 3.2

\(C[a,b]\) ist bezüglich der Integralmetrik

(3.2)\[d(x,y) = \left(\int_a^b |x(t)-y(t)|^p dt \right)^{1/p},\quad 1\le p < \infty\]

nicht vollständig.

Wir betrachten dazu für \(p=2\) auf \(C[0,1]\) folgendes Gegenbeispiel:

Sei \(t\in[0,1]\)

(3.3)\[\begin{split}x_n(t) := \begin{cases} n^\alpha\quad\text{für}\ t \le 1/n\\ \frac{1}{t^\alpha}\quad\text{für}\ t > 1/n\end{cases}\end{split}\]

und \(x(t) = \frac{1}{t^\alpha}\) für \(0<\alpha<1/2\).

Show code cell source Hide code cell source

def xn(t,n,alpha):
    y = np.zeros_like(t)
    y[t<=1/n] = n**alpha
    y[t>1/n] = 1/(t[t>1/n]**alpha)
    return y
x = lambda t, alpha: 1/t**alpha
t = np.linspace(0,1,400)
plt.plot(t,xn(t,3,1/3), label='$n=3$')
plt.plot(t,xn(t,10,1/3), label='$n=10$')
plt.plot(t,xn(t,20,1/3), label='$n=20$')
plt.plot(t[1:],x(t[1:],1/3),'--', label='Grenzfunktion')
plt.title(r'$\alpha = 1/3$')
plt.legend()
plt.ylim(0,4)
plt.show()

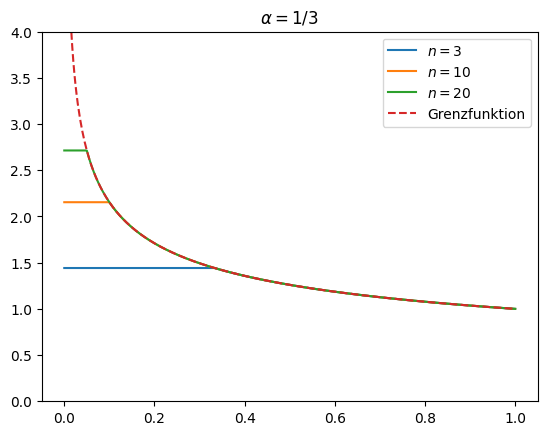
Es gilt \(x_n \in C[0,1]\) für alle \(n\in\mathbb{N}\) und

\[d(x_n,x)^2 = \int_0^1 |x_n(t)-x(t)|^2 dt = \int_0^{1/n} (n^\alpha - t^{-\alpha})^2 dt.\]

Mit Hilfe der Ungleichung \((a-b)^2 \le 2 (a^2+b^2)\) folgt

\[d(x_n,x)^2 \le 2 \int_0^{1/n} (n^{2\alpha} + t^{-2\alpha})^2 dt = \frac{2}{n^{1-2\alpha}} + \frac{2}{1-2\alpha} \frac{1}{n^{1-2\alpha}} \to 0 \quad \text{für}\ n\to\infty\]

da \(1-2\alpha > 0\) gilt. Mit dem konviergiert die Folge \(\{x_n\}\) gegen \(x\) in der Integralmetrik (\(p=2\)). Wir zeigen, dass \(\{x_n(t)\}\) keine auf \([0,1]\) stetige Grenzfunktion besitzt. Dazu nehmen wir an, dass \(y(t)\in C[0,1]\) sei Grenzfunktion der Folge \(\{x_n(t)\}\). Wir setzen

\[M = \max_{0\le t\le 1} |y(t)|.\]

(Muss für eine wohl definierte Obersumme endlich sein!) Für \(t \le (2M)^{-1/\alpha}\) und \(n > (2M)^{1/\alpha}\) gilt

\[x_n(t) - y(t) \ge M\quad \text{für}\quad t\le (2M)^{-1/\alpha}\]

und somit

\[d^2(x_n,y) = \int_0^1 |x_n(t)-y(t)|^2 dt \ge \int_0^{(2M)^{-1/\alpha}} |x_n(t)-y(t)|^2 dt \ge (2M)^{-1/\alpha}\cdot M^2 > 0, \quad \text{für}\quad n > (2M)^{1/\alpha}\]

im Widerspruch zur Annahme, dass \(\{x_n(t)\}\) gegen \(y(t)\) konvergiert. Damit ist die Behauptung bewiesen. \(\Box\)

Die Tatsache, daß \(C[a,b]\), versehen mit einer Integralmetrik, kein vollständiger metrischer Raum ist, bedeutet einen schwerwiegenden Mangel dieses Raumes. Jedoch gibt es mehrere Wege der Vervollständigung (vgl. Kapitel Abschnitt 5.1):

1. Man erweitert die Klasse \(C[a,b]\) zur Klasse der auf \([a,b]\) Lebesgue-integrierbaren Funktionen und interpretiert das in (3.2) auftretende Integral im Lebesgueschen Sinn (vgl. Illustration Lebesgue Integral Abschnitt 3.2.5). Dadurch gelangt man zum vollständigen metrischen Raum \(L_p[a, b]\) (vgl. [Heu08], S. 109).

2. Ein anderer Weg besteht darin, dass der vollständige Erweiterungsraum als Menge von linearen Funktionalen auf einem geeigneten Grundraum nach dem Vorbild der Distributionentheorie aufgefasst wird.

3. Ein weiterer Weg besteht in der abstrakten Konstruktion eines vollständigen Erweiterungsraums mit Hilfe von Cauchy-Folgen. Auf diese Weise lässt sich jeder nichtvollständige metrische Raum vervollständigen (vgl. [Heu06], S. 251)

Wir definieren kompakt für metrische Räume wie folgt

Definition 3.12 (Kompakt)

Sein \(V\) ein metrischer Raum. \(W \subset V\) heisst kompakt, wenn jede Folge \(\{x_n\}\) aus \(W\) eine Teilfolge enthält, die gegen ein Grenzelement \(x\in W\) konvergiert.

Theorem 3.2

Jede kompakte Teilmenge \(W\) eines metrischen Raumes \(V\) ist beschränkt und abgeschlossen.

Die Umkehrung gilt im allgemeinen nicht.

3.2.4. Bestapproximation in metrischen Räumen

In der Approximationstheorie stellt sich das Grundproblem: In einem metrischen Raum \(V\) sei eine Teilmenge \(W\) und ein fester Punkt \(y\in V\) vorgegeben. Zu bestimmen ist ein Punkt \(x_0 \in W\), der von \(y\) minimalen Abstand hat. Das Problem beginnt schon damit, dass es nicht klar, ist, dass es einen solchen Punkt überhaupt gibt:

Beispiel: Betrachte den Raum \((\mathbb{R}, d)\) mit \(d(x_1,x_2) = |x_1-x_2|\). Die Teilmenge \(W\) sei gegeben durch \(W = (0,1)\) und \(y=2\). In \(W\) gibt es keinen Punkt \(x_0\), für den \(d(x_0,2)\) minimal ist (\(1\not\in W\)).

Zur Erinnerung:

Definition 3.13 (Supremum, Infimum)

Sei \(W\subset \mathbb{R}\), dann bezeichnet man mit dem Supremum von \(W\) die kleinste reelle Zahl \(\lambda\) mit \(x\le \lambda\) für alle \(x\in W\). Analog bezeichnet man mit dem Infimum die grösste reelle Zahl \(\mu\) mit \(x\ge \mu\) für alle \(x\in W\).

Theorem 3.3

Es sei \(V\) ein metrischer Raum und \(W\) eine kompakte Teilmenge von \(V\). Dann gibt es zu jedem festen Punkt \(y \in V\) einen Punkt \(x_0 \in W\), der von \(y\) kleinsten Abstand hat.

Betrachten wir das obige Beispiel angepasst auf die Voraussetzung im Satz: Sei \(W = [0,1] \subset \mathbb{R}\) ein kompaktes Intervall, dann ist der Punkt \(x_0 = 1\) bestapproximierendes Element.

Abb. 3.1 Bestapproximation