9.2.3. Element Matrizen 1d Fall

Lagrange Polynome als Basisfunktionen

Show code cell content Hide code cell content

import numpy as np
import matplotlib.pyplot as plt

from sympy import integrate
from sympy.abc import x

from pandas import DataFrame
from IPython.display import display

def highlight_ortho(s):
    is_ortho = np.abs(s) < 1e-13
    return ['background-color: yellow' if v else '' for v in is_ortho]

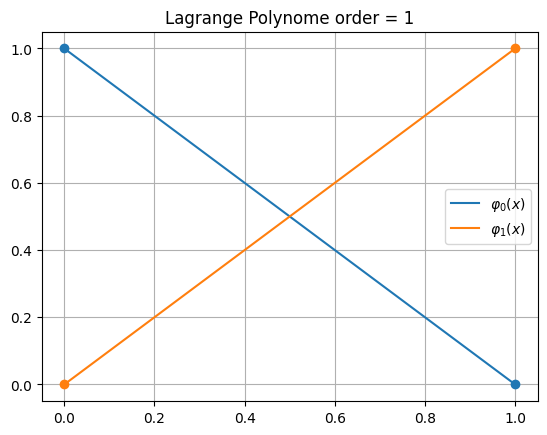
Wir benutzen Lagrange Polynome

\[\varphi_j(x) = \prod_{i\not=j}^n \frac{x-x_i}{x_j-x_i}\]

verschiedener Ordnung als FEM Basis Funktionen:

def lagrangePoly(x,j,order):
    xi = np.linspace(0,1,order+1)
    J = np.delete(np.arange(order+1),j)
    return np.prod([(x-xi[i])/(xi[j]-xi[i]) for i in J],axis=0)

Die Polynome sind gegeben durch:

Show code cell source Hide code cell source

maxorder = 4
for order in range(1,maxorder+1):
    print('Order = ',order)
    for i in range(order+1):
        display(lagrangePoly(x,i,order).expand())

Order =  1

\[\displaystyle 1.0 - 1.0 x\]

\[\displaystyle 1.0 x\]

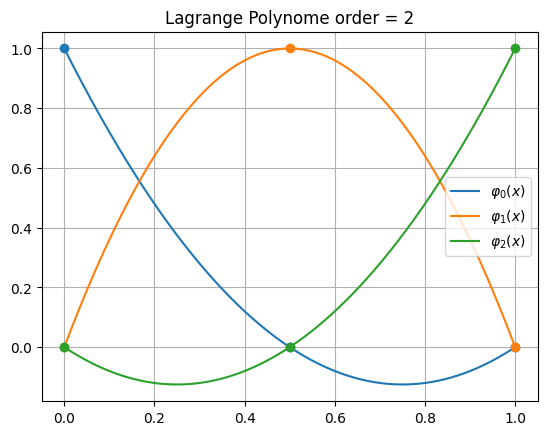
Order =  2

\[\displaystyle 2.0 x^{2} - 3.0 x + 1.0\]

\[\displaystyle - 4.0 x^{2} + 4.0 x\]

\[\displaystyle 2.0 x^{2} - 1.0 x\]

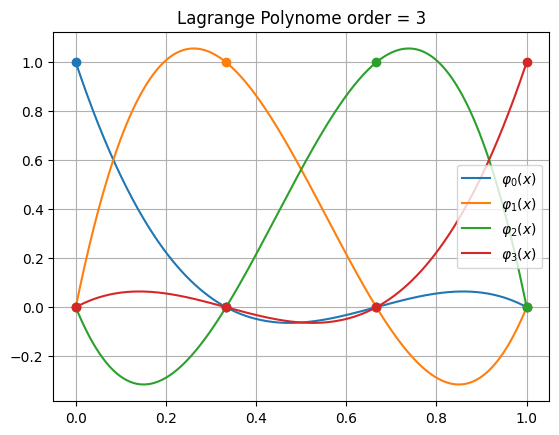
Order =  3

\[\displaystyle - 4.5 x^{3} + 9.0 x^{2} - 5.5 x + 1.0\]

\[\displaystyle 13.5 x^{3} - 22.5 x^{2} + 9.0 x\]

\[\displaystyle - 13.5 x^{3} + 18.0 x^{2} - 4.5 x\]

\[\displaystyle 4.5 x^{3} - 4.5 x^{2} + 1.0 x\]

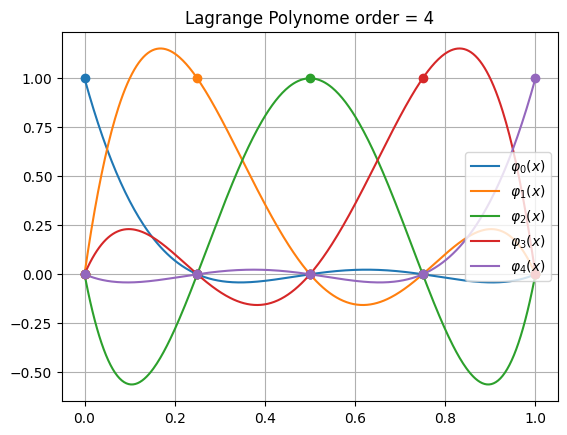
Order =  4

\[\displaystyle 10.6666666666667 x^{4} - 26.6666666666667 x^{3} + 23.3333333333333 x^{2} - 8.33333333333333 x + 1.0\]

\[\displaystyle - 42.6666666666667 x^{4} + 96.0 x^{3} - 69.3333333333333 x^{2} + 16.0 x\]

\[\displaystyle 64.0 x^{4} - 128.0 x^{3} + 76.0 x^{2} - 12.0 x\]

\[\displaystyle - 42.6666666666667 x^{4} + 74.6666666666667 x^{3} - 37.3333333333333 x^{2} + 5.33333333333333 x\]

\[\displaystyle 10.6666666666667 x^{4} - 16.0 x^{3} + 7.33333333333333 x^{2} - 1.0 x\]

Show code cell source Hide code cell source

xp = np.linspace(0,1,400)
col = ['tab:blue','tab:orange','tab:green','tab:red','tab:purple','tab:brown','tab:pink']
for order in range(1,maxorder+1):
    xi = np.linspace(0,1,order+1)
    for j in range(order+1):
        plt.plot(xp,lagrangePoly(xp,j,order),c=col[j],label=r'$\varphi_'+str(j)+'(x)$')
        plt.plot(xi,lagrangePoly(xi,j,order),'o',c=col[j])
    plt.legend(loc=5)
    plt.grid()
    plt.title('Lagrange Polynome order = '+str(order))
    plt.show()

Für die Steifigkeit-Elementmatrizen

\[A_{i,j} = \int_0^1 \varphi_i'(x) \varphi_j'(x) dx\]

erhalten wir

Show code cell source Hide code cell source

for order in range(1,maxorder+1):
    print('order = ',order)
    m = [[integrate(lagrangePoly(x,i,order).diff()*lagrangePoly(x,j,order).diff(),(x,0,1))
                     for i in range(order+1)] for j in range(order+1)]
    df = DataFrame(m)
    display(df.style.\
        apply(highlight_ortho).\
        set_table_attributes('style="font-size: 12px"').\
        format('{:.3f}'))

order =  1

	0	1
0	1.000	-1.000
1	-1.000	1.000

order =  2

	0	1	2
0	2.333	-2.667	0.333
1	-2.667	5.333	-2.667
2	0.333	-2.667	2.333

order =  3

	0	1	2	3
0	3.700	-4.725	1.350	-0.325
1	-4.725	10.800	-7.425	1.350
2	1.350	-7.425	10.800	-4.725
3	-0.325	1.350	-4.725	3.700

order =  4

	0	1	2	3	4
0	5.212	-7.247	3.225	-1.558	0.367
1	-7.247	17.608	-15.035	6.231	-1.558
2	3.225	-15.035	23.619	-15.035	3.225
3	-1.558	6.231	-15.035	17.608	-7.247
4	0.367	-1.558	3.225	-7.247	5.212

Für die Massen-Elementmatrizen

\[M_{i,j} = \int_0^1 \varphi_i(x) \varphi_j(x) dx\]

erhalten wir

Show code cell source Hide code cell source

for order in range(1,maxorder+1):
    print('order = ',order)
    m = [[integrate(lagrangePoly(x,i,order)*lagrangePoly(x,j,order),(x,0,1))
                     for i in range(order+1)] for j in range(order+1)]
    df = DataFrame(m)
    display(df.style.\
        apply(highlight_ortho).\
        set_table_attributes('style="font-size: 12px"').\
        format('{:.3f}'))

order =  1

	0	1
0	0.333	0.167
1	0.167	0.333

order =  2

	0	1	2
0	0.133	0.067	-0.033
1	0.067	0.533	0.067
2	-0.033	0.067	0.133

order =  3

	0	1	2	3
0	0.076	0.059	-0.021	0.011
1	0.059	0.386	-0.048	-0.021
2	-0.021	-0.048	0.386	0.059
3	0.011	-0.021	0.059	0.076

order =  4

	0	1	2	3	4
0	0.051	0.052	-0.031	0.010	-0.005
1	0.052	0.316	-0.068	0.045	0.010
2	-0.031	-0.068	0.330	-0.068	-0.031
3	0.010	0.045	-0.068	0.316	0.052
4	-0.005	0.010	-0.031	0.052	0.051

Hierarchische Basis Polynome

NGSolve benutzt für die finite Elemente Räume höherer Ordnung immer die Basisfunktionen aus den Räumen niederer Ordnung und erweitert diese entsprechend.

Show code cell source Hide code cell source

from netgen.meshing import Mesh as NGMesh # Vorsicht es gibt Mesh auch in ngsolve!
from netgen.meshing import MeshPoint, Pnt, Element1D, Element0D
from ngsolve import *

m = NGMesh(dim=1)

# Punkte für die Zerlegung auf dem Intervall [0,1]
pnums = []
pnums.append (m.Add (MeshPoint (Pnt(0, 0, 0))))
pnums.append (m.Add (MeshPoint (Pnt(1, 0, 0))))

# Jedes 1D-Element (Teilintervall) kann einem Material zugeordnet
# werden. In unserem Fall gibt es nur ein Material.
idx = m.AddRegion("material", dim=1)
m.Add (Element1D ([pnums[0],pnums[1]], index=idx))

# Linkes und Rechtes Ende sind Randwertpunkte (0D-Elemente)
idx_left = m.AddRegion("left", dim=0)
idx_right = m.AddRegion("right", dim=0)

m.Add (Element0D (pnums[0], index=idx_left))
m.Add (Element0D (pnums[1], index=idx_right))

# Damit haben wir das Mesh definiert
mesh = Mesh(m)

xp = np.linspace(0,1,300)
for order in range(1,maxorder+1):
    V = H1(mesh,order = order, dirichlet='left|right')
    gfu = GridFunction(V)

    for k in range(V.ndof):
        gfu.vec[:] = 0
        gfu.vec[k] = 1
        plt.plot(xp,gfu(mesh(xp)),label=r'$\varphi_'+str(k)+'$')
    plt.legend()
    plt.title('order = '+str(order))
    plt.grid()
    plt.show()

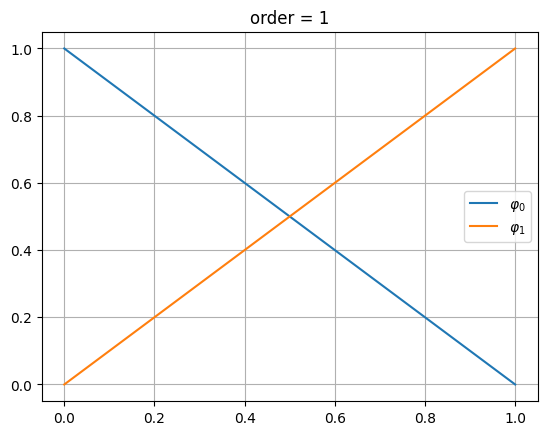
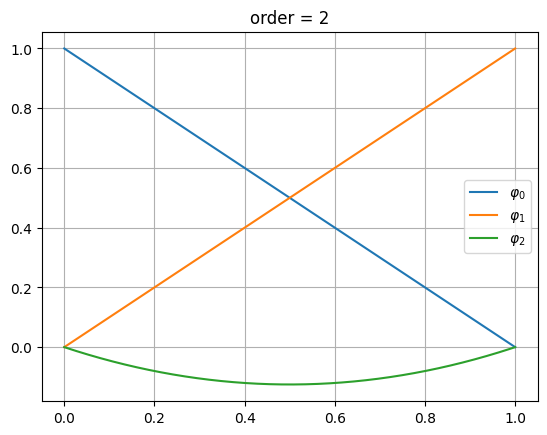
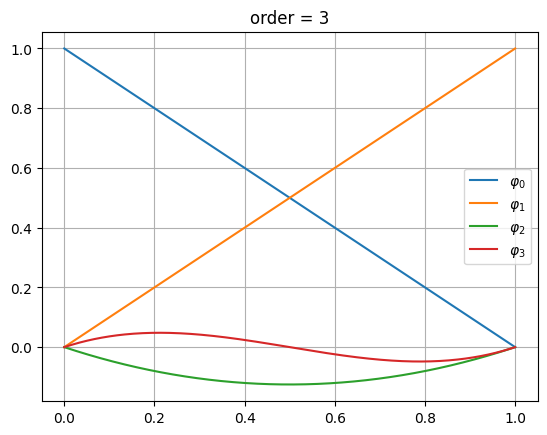
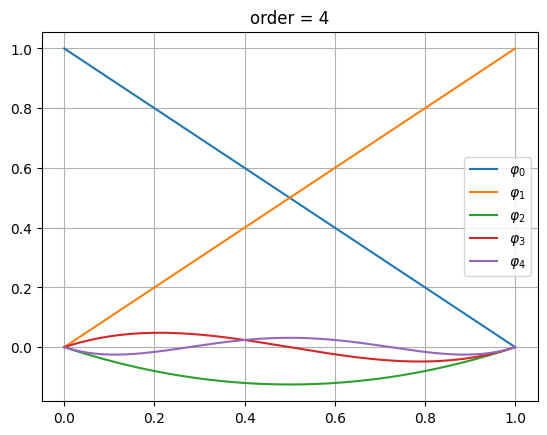
Für die Steifigkeit-Elementmatrizen

\[A_{i,j} = \int_0^1 \varphi_i'(x) \varphi_j'(x) dx\]

erhalten wir

Show code cell source Hide code cell source

for order in range(1,maxorder+1):
    print('order = ',order)
    V = H1(mesh,order = order, dirichlet='left|right')
    gfu = GridFunction(V)

    phii = GridFunction(V)
    phij = GridFunction(V)

    a = []
    for i in range(V.ndof):
        phii.vec[:]=0
        phii.vec[i]=1
        ai = []
        for j in range(V.ndof):
            phij.vec[:]=0
            phij.vec[j]=1
            ai.append(Integrate(grad(phii)*grad(phij),mesh,order=2*order))
        a.append(ai)

    df = DataFrame(a)
    display(df.style.\
        apply(highlight_ortho).\
        set_table_attributes('style="font-size: 12px"').\
        format('{:.4f}'))

order =  1

	0	1
0	1.0000	-1.0000
1	-1.0000	1.0000

order =  2

	0	1	2
0	1.0000	-1.0000	0.0000
1	-1.0000	1.0000	0.0000
2	0.0000	0.0000	0.0833

order =  3

	0	1	2	3
0	1.0000	-1.0000	0.0000	0.0000
1	-1.0000	1.0000	0.0000	-0.0000
2	0.0000	0.0000	0.0833	0.0000
3	0.0000	-0.0000	0.0000	0.0500

order =  4

	0	1	2	3	4
0	1.0000	-1.0000	0.0000	0.0000	-0.0000
1	-1.0000	1.0000	0.0000	-0.0000	0.0000
2	0.0000	0.0000	0.0833	0.0000	-0.0000
3	0.0000	-0.0000	0.0000	0.0500	0.0000
4	-0.0000	0.0000	-0.0000	0.0000	0.0357

Für die Massen-Elementmatrizen

\[M_{i,j} = \int_0^1 \varphi_i(x) \varphi_j(x) dx\]

erhalten wir

Show code cell source Hide code cell source

for order in range(1,maxorder+1):
    print('order = ',order)
    V = H1(mesh,order = order, dirichlet='left|right')
    gfu = GridFunction(V)

    phii = GridFunction(V)
    phij = GridFunction(V)

    b = []
    for i in range(V.ndof):
        phii.vec[:]=0
        phii.vec[i]=1
        bi = []
        for j in range(V.ndof):
            phij.vec[:]=0
            phij.vec[j]=1
            bi.append(Integrate(phii*phij,mesh,order=2*order))
        b.append(bi)

    df = DataFrame(b)
    display(df.style.\
        apply(highlight_ortho).\
        set_table_attributes('style="font-size: 12px"').\
        format('{:.3f}'))

order =  1

	0	1
0	0.333	0.167
1	0.167	0.333

order =  2

	0	1	2
0	0.333	0.167	-0.042
1	0.167	0.333	-0.042
2	-0.042	-0.042	0.008

order =  3

	0	1	2	3
0	0.333	0.167	-0.042	0.008
1	0.167	0.333	-0.042	-0.008
2	-0.042	-0.042	0.008	-0.000
3	0.008	-0.008	-0.000	0.001

order =  4

	0	1	2	3	4
0	0.333	0.167	-0.042	0.008	0.000
1	0.167	0.333	-0.042	-0.008	0.000
2	-0.042	-0.042	0.008	-0.000	-0.001
3	0.008	-0.008	-0.000	0.001	-0.000
4	0.000	0.000	-0.001	-0.000	0.000