9.2.6. 2d - Beispiel zum Assembling#
Wir betrachten als Beispiel das zum 1d analoge Problem
mit Dirichlet Randwerten und \(f(x) \equiv 1\). Die schwache Gleichung ist gegeben durch
Definition des Gebiets und Meshes#
Die Definition des Gebiets und Meshes wird nun etwas aufwändiger. Wir definieren zuerst die Knoten und danach darauf basierend die einzelnen Dreiecke. Das Mesh besteht daher aus einer Menge von Dreiecken, für welche \(\Omega = \cup_i T_i\) gilt.
import numpy as np
import matplotlib.pyplot as plt
from pandas import DataFrame
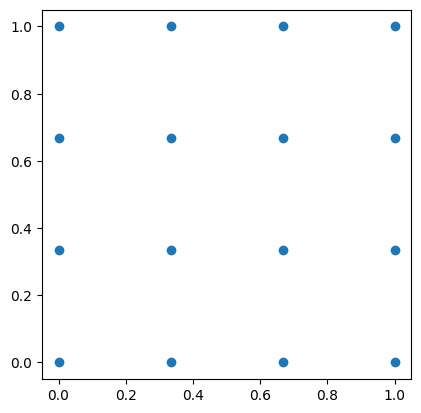
Die Punkte verteilen wir kartesisch auf dem Gebiet \(\Omega = [0,1]^2\):
n = 3# Anzahl Intervalle in x/y Richtung
xi = np.linspace(0,1,n+1)
yi = np.linspace(0,1,n+1)
Xi,Yi = np.meshgrid(xi,yi)
pts = np.array([Xi.flatten(),Yi.flatten()]).T
Damit folgt
plt.plot(*pts.T,'o')
plt.gca().set_aspect(1)
plt.show()
Nun müssen die Dreiecke definiert werden. Es gilt
T = []
for i in range(n):
for j in range(n):
# in jedem Quadrat gilt
# 1. Dreieck 1. Punkt, 2. Punkt, 3. Punkt (Nummer)
T.append([ i*(n+1)+j, i*(n+1)+j+1, (i+1)*(n+1)+j])
# 2. Dreieck 1. Punkt, 2. Punkt, 3. Punkt
T.append([ i*(n+1)+j+1, (i+1)*(n+1)+j+1, (i+1)*(n+1)+j])
T = np.array(T)
T = np.reshape(T, (-1,3))
T
array([[ 0, 1, 4],
[ 1, 5, 4],
[ 1, 2, 5],
[ 2, 6, 5],
[ 2, 3, 6],
[ 3, 7, 6],
[ 4, 5, 8],
[ 5, 9, 8],
[ 5, 6, 9],
[ 6, 10, 9],
[ 6, 7, 10],
[ 7, 11, 10],
[ 8, 9, 12],
[ 9, 13, 12],
[ 9, 10, 13],
[10, 14, 13],
[10, 11, 14],
[11, 15, 14]])
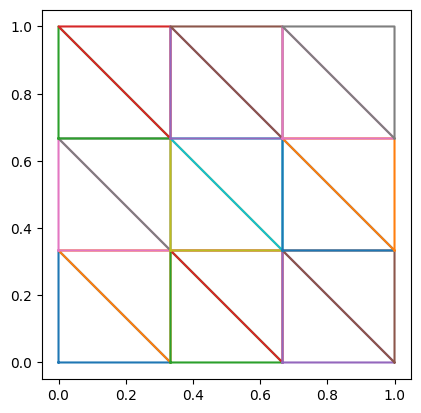
Damit folgt das Mesh
for t in T:
plt.plot(*pts[t.tolist()+[t[0]]].T)
plt.gca().set_aspect(1)
plt.show()
FE-Space mit Elemente 1. Ordnung#
# Basisfunktionen auf dem Referenzelement
def myshape(t, j):
xi, eta = t
if j == 0:
return 1-xi-eta
elif j == 1:
return xi
else:
return eta
# Gradienten der Basisfunktionen auf dem Referenzelement
def Dmyshape(t, j):
if j == 0:
return np.array([-1,-1])
elif j == 1:
return np.array([1,0])
else:
return np.array([0,1])
Pro Element gibt es drei Basisfunktionen. Wobei die Anzahlfreiheitsgrade aufgrund der Stetigkeitsbedingung durch die Anzahl Knoten gegeben ist. Damit folgt
len(pts)
16
Für die Integration über das Einheitsdreieck nutzen wir die numerische Integration aus scipy
from scipy.integrate import dblquad
# Integration über Einheitsdreieck
def quadT(f):
return dblquad(f,0,1,0,lambda xi: 1-xi)[0]
Die Koordinaten Transformation ist gegeben durch
und entsprechend die inverse Transformation
def sigma(p1,p2,p3):
At = np.array([(p2-p1),(p3-p1)]).T
return (lambda xi, eta: p1+At@(np.array([xi,eta])))
def invsigma(p1,p2,p3):
At = np.array([(p2-p1),(p3-p1)]).T
adjAt = np.array([[At[1,1],-At[0,1]],[-At[1,0],At[0,0]]])
detAt = np.linalg.det(At)
invAt = adjAt/detAt
return (lambda x, y: invAt@(np.array([xi,eta])-p1))
def CnJ(p1,p2,p3):
A = np.array([(p2-p1),(p3-p1)]).T
adjA = np.array([[A[1,1],-A[0,1]],[-A[1,0],A[0,0]]])
detA = np.linalg.det(A)
invA = adjA/detA
return invA@invA.T, detA
Assembling der globalen Systemmatrix und -vektor#
Wir berechnen daher das Gleichungssystem der diskreten schwachen Gleichung. Dazu benötigen wir die Funktion \(f(x)\)
def myfun(x,y):
return 1
#return np.sin(x*y) # x,y abhängiges Beispiel
Show code cell source
def niceprint(A,t):
df = DataFrame(A)
highlights = np.zeros((N,N),dtype=bool)
highlights[np.ix_(t,t)] = True
cell_color = DataFrame(highlights)
s = df.style.format('{:.2f}').set_table_styles([{'selector': '.True', 'props': [('background-color', 'yellow')]}], overwrite=True)
s.set_td_classes(cell_color)
display(s)
return
N = pts.shape[0]
A = np.zeros((N,N),dtype=float)
f = np.zeros(N,dtype=float)
# Assembling
for k,t in enumerate(T):
Ci, Ji = CnJ(*pts[t])
si = sigma(*pts[t])
# lokale Elementmatrix, Integration der shape und dshape function über das Einheitsdreieck
Ai = np.array([[quadT(lambda xi, eta: Dmyshape([xi,eta],i)@Ci@Dmyshape([xi,eta],j)*Ji)
for j in range(3)]
for i in range(3)])
Mi = np.array([[quadT(lambda xi, eta: 10*myshape([xi,eta],i)*myshape([xi,eta],j)*Ji)
for j in range(3)]
for i in range(3)])
# Speichern in der globalen Matrix
A[np.ix_(t,t)] += Ai#+Mi
print('Element',k)
print('lokale Elementmatrix')
display(DataFrame(Ai).style.format('{:.2f}'))
print('globale Matrix')
niceprint(A,t)
# lokale Linearform
fi = np.array([quadT(lambda xi, eta: myfun(*si(xi,eta))*myshape([xi,eta],j)*Ji) for j in range(3)])
f[t] += fi
Show code cell output
Element 0
lokale Elementmatrix
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 1.00 | -0.50 | -0.50 |
| 1 | -0.50 | 0.50 | 0.00 |
| 2 | -0.50 | 0.00 | 0.50 |
globale Matrix
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | -0.50 | 0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 4 | -0.50 | 0.00 | 0.00 | 0.00 | 0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 6 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Element 1
lokale Elementmatrix
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 0.50 | -0.50 | 0.00 |
| 1 | -0.50 | 1.00 | -0.50 |
| 2 | 0.00 | -0.50 | 0.50 |
globale Matrix
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 4 | -0.50 | 0.00 | 0.00 | 0.00 | 1.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.00 | -0.50 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 6 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Element 2
lokale Elementmatrix
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 1.00 | -0.50 | -0.50 |
| 1 | -0.50 | 0.50 | 0.00 |
| 2 | -0.50 | 0.00 | 0.50 |
globale Matrix
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | -0.50 | 0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 4 | -0.50 | 0.00 | 0.00 | 0.00 | 1.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 1.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 6 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Element 3
lokale Elementmatrix
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 0.50 | -0.50 | 0.00 |
| 1 | -0.50 | 1.00 | -0.50 |
| 2 | 0.00 | -0.50 | 0.50 |
globale Matrix
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 4 | -0.50 | 0.00 | 0.00 | 0.00 | 1.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 6 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Element 4
lokale Elementmatrix
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 1.00 | -0.50 | -0.50 |
| 1 | -0.50 | 0.50 | 0.00 |
| 2 | -0.50 | 0.00 | 0.50 |
globale Matrix
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | -0.50 | 0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 4 | -0.50 | 0.00 | 0.00 | 0.00 | 1.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 6 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 1.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Element 5
lokale Elementmatrix
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 0.50 | -0.50 | 0.00 |
| 1 | -0.50 | 1.00 | -0.50 |
| 2 | 0.00 | -0.50 | 0.50 |
globale Matrix
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 4 | -0.50 | 0.00 | 0.00 | 0.00 | 1.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 6 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Element 6
lokale Elementmatrix
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 1.00 | -0.50 | -0.50 |
| 1 | -0.50 | 0.50 | 0.00 |
| 2 | -0.50 | 0.00 | 0.50 |
globale Matrix
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 4 | -0.50 | 0.00 | 0.00 | 0.00 | 2.00 | -1.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 2.50 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 6 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Element 7
lokale Elementmatrix
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 0.50 | -0.50 | 0.00 |
| 1 | -0.50 | 1.00 | -0.50 |
| 2 | 0.00 | -0.50 | 0.50 |
globale Matrix
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 4 | -0.50 | 0.00 | 0.00 | 0.00 | 2.00 | -1.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 3.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 6 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 1.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Element 8
lokale Elementmatrix
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 1.00 | -0.50 | -0.50 |
| 1 | -0.50 | 0.50 | 0.00 |
| 2 | -0.50 | 0.00 | 0.50 |
globale Matrix
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 4 | -0.50 | 0.00 | 0.00 | 0.00 | 2.00 | -1.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 6 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 2.50 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 1.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 1.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Element 9
lokale Elementmatrix
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 0.50 | -0.50 | 0.00 |
| 1 | -0.50 | 1.00 | -0.50 |
| 2 | 0.00 | -0.50 | 0.50 |
globale Matrix
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 4 | -0.50 | 0.00 | 0.00 | 0.00 | 2.00 | -1.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 6 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 3.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 1.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Element 10
lokale Elementmatrix
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 1.00 | -0.50 | -0.50 |
| 1 | -0.50 | 0.50 | 0.00 |
| 2 | -0.50 | 0.00 | 0.50 |
globale Matrix
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 4 | -0.50 | 0.00 | 0.00 | 0.00 | 2.00 | -1.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 6 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -1.00 | 1.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 1.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 1.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Element 11
lokale Elementmatrix
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 0.50 | -0.50 | 0.00 |
| 1 | -0.50 | 1.00 | -0.50 |
| 2 | 0.00 | -0.50 | 0.50 |
globale Matrix
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 4 | -0.50 | 0.00 | 0.00 | 0.00 | 2.00 | -1.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 6 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -1.00 | 2.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 1.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Element 12
lokale Elementmatrix
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 1.00 | -0.50 | -0.50 |
| 1 | -0.50 | 0.50 | 0.00 |
| 2 | -0.50 | 0.00 | 0.50 |
globale Matrix
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 4 | -0.50 | 0.00 | 0.00 | 0.00 | 2.00 | -1.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 6 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -1.00 | 2.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 2.00 | -1.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 2.50 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.50 | 0.00 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Element 13
lokale Elementmatrix
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 0.50 | -0.50 | 0.00 |
| 1 | -0.50 | 1.00 | -0.50 |
| 2 | 0.00 | -0.50 | 0.50 |
globale Matrix
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 4 | -0.50 | 0.00 | 0.00 | 0.00 | 2.00 | -1.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 6 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -1.00 | 2.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 2.00 | -1.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 3.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 1.00 | -0.50 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Element 14
lokale Elementmatrix
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 1.00 | -0.50 | -0.50 |
| 1 | -0.50 | 0.50 | 0.00 |
| 2 | -0.50 | 0.00 | 0.50 |
globale Matrix
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 4 | -0.50 | 0.00 | 0.00 | 0.00 | 2.00 | -1.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 6 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -1.00 | 2.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 2.00 | -1.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 2.50 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 1.00 | -0.50 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 1.50 | 0.00 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Element 15
lokale Elementmatrix
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 0.50 | -0.50 | 0.00 |
| 1 | -0.50 | 1.00 | -0.50 |
| 2 | 0.00 | -0.50 | 0.50 |
globale Matrix
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 4 | -0.50 | 0.00 | 0.00 | 0.00 | 2.00 | -1.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 6 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -1.00 | 2.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 2.00 | -1.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 3.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 1.00 | -0.50 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Element 16
lokale Elementmatrix
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 1.00 | -0.50 | -0.50 |
| 1 | -0.50 | 0.50 | 0.00 |
| 2 | -0.50 | 0.00 | 0.50 |
globale Matrix
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 4 | -0.50 | 0.00 | 0.00 | 0.00 | 2.00 | -1.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 6 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -1.00 | 2.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 2.00 | -1.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -1.00 | 1.50 | 0.00 | 0.00 | 0.00 | 0.00 |
| 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 1.00 | -0.50 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 1.50 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Element 17
lokale Elementmatrix
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 0.50 | -0.50 | 0.00 |
| 1 | -0.50 | 1.00 | -0.50 |
| 2 | 0.00 | -0.50 | 0.50 |
globale Matrix
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.00 | -0.50 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | -0.50 | 1.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 4 | -0.50 | 0.00 | 0.00 | 0.00 | 2.00 | -1.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 6 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -1.00 | 2.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 0.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 2.00 | -1.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -1.00 | 4.00 | -1.00 | 0.00 | 0.00 | -1.00 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -1.00 | 2.00 | 0.00 | 0.00 | 0.00 | -0.50 |
| 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | 0.00 | 1.00 | -0.50 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 2.00 | -0.50 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -1.00 | 0.00 | 0.00 | -0.50 | 2.00 | -0.50 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -0.50 | 0.00 | 0.00 | -0.50 | 1.00 |
Lösen des Systems#
Definieren der freien Freiheitsgrade, abhängig von den Randbedingungen
freedofs = []#np.array([4,5,7,8])
for k in range(1,n):
freedofs += np.arange(k*(n+1)+1,(k+1)*(n+1)-1,dtype=int).tolist()
freedofs = np.array(freedofs)
print('freedofs=',freedofs)
sol = np.zeros(N)
sol[freedofs] = np.linalg.solve(A[np.ix_(freedofs,freedofs)],f[freedofs])
sol
freedofs= [ 5 6 9 10]
array([0. , 0. , 0. , 0. , 0. ,
0.05555556, 0.05555556, 0. , 0. , 0.05555556,
0.05555556, 0. , 0. , 0. , 0. ,
0. ])
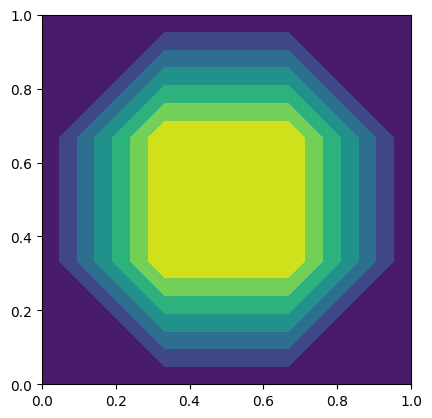
plt.contourf(pts[:,0].reshape((n+1,n+1)),pts[:,1].reshape((n+1,n+1)),sol.reshape((n+1,n+1)))
plt.gca().set_aspect(1)
Äquivalente Lösung mit Hilfe von NGSolve#
from ngsolve import *
from ngsolve.meshes import MakeStructured2DMesh
from ngsolve.webgui import Draw
Mesh erstellen
mesh = MakeStructured2DMesh(quads=False, nx = n, ny=n, mapping = lambda x,y: (x,y))
Draw(mesh)
BaseWebGuiScene
Namen der Ränder:
mesh.GetBoundaries()
('bottom', 'right', 'top', 'left')
Definition des FE-Space, Bilinearform und Linearform sowie der Lösung
V = H1(mesh, order=1, dirichlet='bottom|right|top|left')
u,v = V.TnT()
gfu = GridFunction(V)
a = BilinearForm(V)
a += grad(u)*grad(v)*dx
a.Assemble()
b = LinearForm(V)
b += 1*v*dx(bonus_intorder=5)
b.Assemble()
gfu.vec.data = a.mat.Inverse(freedofs=V.FreeDofs())*b.vec
Die Anzahl Freiheitsgrade ist gegeben durch
V.ndof
16
Unsere freien Freiheitsgrade sind gegeben durch:
freedofs
array([ 5, 6, 9, 10])
In NGSolve erhalten wir
print(V.FreeDofs())
0: 0000011001100000
Unser Lösungsvektor ist gegeben durch
print(sol)
[0. 0. 0. 0. 0. 0.05555556
0.05555556 0. 0. 0.05555556 0.05555556 0.
0. 0. 0. 0. ]
Die Lösung von NGSolve ist identisch:
print(np.array(gfu.vec))
[0. 0. 0. 0. 0. 0.05555556
0.05555556 0. 0. 0.05555556 0.05555556 0.
0. 0. 0. 0. ]
Draw(gfu,mesh)
BaseWebGuiScene
