Normierte Räume. Banachräume

Inhalt

3.3. Normierte Räume. Banachräume#

3.3.1. Banachräume#

Bis jetzt haben wir sehr wenig Eigenschaften eines Raumes benötigt. Was uns noch fehlt, sind abgesehen vom Abstand der Elemente noch algebraische Eigenschaften (addieren, multiplizieren, etc.). Dazu definieren wir den linearen Raum (oder Vektorraum) wie folgt. Im folgenden sei der Körper $\mathbb{K}$ immer der Körper $\mathbb{R}$ oder $\mathbb{C}$ der reellen bzw. komplexen Zahlen.

Definition 3.14 (linearer Raum)

Ein linearer Raum (oder Vektorraum) über einem Körper $\mathbb{K}$ besteht aus einer nichtleeren Menge $V$, sowie

einer Vorschrift, die jedem Paar $(x,y)$ mit $x,y \in V$ genau ein Element $x+y\in V$ zuordnet (Addition)
einer Vorschrift, die jedem Paar $(\lambda,x)$ mit $\lambda\in \mathbb{K}$ und $x \in V$ genau ein Element $\lambda x\in V$ zuordnet (Multiplikation mit Skalaren), wobei für alle $x,y,z \in V$ und $\lambda, \mu\in\mathbb{K}$ folgende Regeln gelten:

\[\begin{split}\begin{array}{rcll} x + (y+z) & = & (x+y) + z & \quad\text{Assoziativgesetz} \\ x + y & = & y + x & \quad\text{Kommutativgesetz} \\ x + 0 & = & x & \quad\text{Nullelement} \\ x + x' & = & 0 & \quad\text{Negatives zu $x$}\\ (\lambda + \mu) x & = & \lambda x + \mu x & \quad\text{1. Distributivgesetz}\\ \lambda (x+y) & = & \lambda x + \lambda y & \quad\text{2. Distributivgesetz}\\ (\lambda \mu) x & = & \lambda (\mu x) & \quad\text{Assoziativgesetz}\\ 1 x & = & x & \quad\text{mit $1\in\mathbb{K}$} \end{array}\end{split}\]

Beispiele für lineare Räume:

Die Mengen $\mathbb{R}^n$, $\mathbb{C}^n$ sind wohl bekannt.
Menge $C[a,b]$ aller reellwertigen stetigen Funktionen:

\[\begin{split}\begin{split} (x+y)(t) & = x(t) + y(t)\\ (\lambda x)(t) & = \lambda x(t)\\ 0(t) & = 0\\ (-x)(t) & = -x(t) \end{split}\end{split}\]

mit $t \in [a,b]\subset \mathbb{R}$, $\lambda\in\mathbb{R}$.
$C^k[a,b]$ Menge aller reellwertigen $k$-mal stetig differenzierbare Funktionen.
$C^{\infty}[a,b]$ Menge aller beliebig oft stetig differenzierbare Funktionen.
Menge aller Polynome
Menge $l_p$ aller Zahlenfolgen $x = \{x_k\}_{k\in\mathbb{N}}$, für die $\sum_{k=1}^{\infty} |x_k|^p < \infty$ konvergiert:

\[\begin{split}\begin{split} x+y & = \{x_k\}_{k\in\mathbb{N}} + \{y_k\}_{k\in\mathbb{N}} = \{x_k + y_k\}_{k\in\mathbb{N}}\\ \lambda x & = \lambda \{x_k\}_{k\in\mathbb{N}} = \{\lambda x_k\}_{k\in\mathbb{N}},\quad \lambda\in\mathbb{R}\end{split}\end{split}\]

Wie in der linearen Algebra sind folgende Begriffe analog definiert

Definition 3.15 (Unterraum, lineare Mannigfaltigkeit, lineare Hülle / Span, linear unabhängig, Dimension, Basis)

Eine nicht leere Teilmenge $S$ von $V$ heisst Unterraum von $V$, wenn für bel. $x,y \in S$ und $\lambda \in \mathbb{K}$ stets

\[x+y \in S\quad\text{und}\quad \lambda x \in S\]

folgt. Insbesondere ist $S$ selbst ein linearer Raum über $\mathbb{K}$.
Ist $S$ ein Unterraum von $V$ und $x_0\in V$ beliebig, so nennt man

\[M = x_0 + S := \{x_0+y\ |\ y\in S\}\]

eine lineare Mannigfaltigkeit von $V$.
Ist $A$ eine beliebige nichtleere Teilmenge von $V$, so bilden alle Linearkombinationen $\sum_{k=1}^m \lambda_k x_k$ mit beliebigem $m \in \mathbb{N}$, $\lambda_k\in\mathbb{K}$, $x_k \in A$ einen Unterraum $S\subset V$. Er wird lineare Hülle von $A$ oder $\mathop{span} A := S$ genannt.

Man sagt: $A$ spannt $S$ auf oder $A$ ist ein Erzeugendensystem von $S$. Im Falle $S=V$ spannt $A$ den ganzen Raum $V$ auf.
Sind $S$ und $T$ Unterräume von $V$, dann ist die Summe $S+T$ definiert durch

\[S+T := \mathop{span} S \cup T.\]
Die (endlich vielen) Elemente $x_1, \ldots, x_n\in V$ heissen linear unabhängig, wenn aus

\[\alpha_1 x_1 + \ldots + \alpha_n x_n = 0\quad\text{stets}\quad \alpha_1 = \ldots = \alpha_n = 0\]

folgt.
Sei $S$ ein Unterraum von $V$. Wir sagen, $S$ besitzt die Dimension $n$, $\mathop{dim} S = n$, wenn es $n$ linear unabhängige Elemente von $S$ gibt, aber $n+1$ Elemente von $S$ stets linear abhängig sind.

$S$ heisst Basis von $V$, wenn die Elemente von $S$ linear unabhängigsind und $\mathop{span} S = V$ gilt.

Besitzt $V$ keine endlich dimensionale Basis, nennt man $V$ unendlich-dimeansional $(\mathop{dim} V = \infty)$.

Bemerkung 3.3

Die oben erwähnten Funktionenräume $C[a,b]$, $C^k[a,b]$, Polynome sind unendlich-dimensional. Ebenso ist der Folgenraum $l_p$ unendlich-dimensional:

Man betrachte

\[x^{(k)} = \{0, \ldots, 0, 1, 0, \ldots \}\in l_p\]

mit 1 an der Stelle $k$.

Im folgenden sind wir an Räumen interessiert, für welche eine lineare Struktur und eine Metrik gegeben ist.

Definition 3.16 (normierter Raum)

Sei $V$ ein metrischer und linearer Raum. Zu dem sei die Metrik $d$ von $V$ translationsinvariant

\[d(x+z, y+z) = d(x,y)\quad\forall\ x,y,z\in V\]

und homogen

\[d(\alpha x, \alpha y) = |\alpha| d(x,y)\quad \forall\ \alpha\in\mathbb{K}, x,y\in V.\]

Dann nennt man $V$ einen normierten Raum. Der durch

\[\|x\| := d(x,0)\quad \forall\ x\in V\]

erklärte Ausdruck heisst Norm von $x$.

Bemerkung 3.4

Neben der kurzen Schreibweise $V$, verwendet man häufig auch die Bezeichnung $(V, \|\cdot\|)$. Der Punkt in $\|\cdot\|$ ist als Platzhalter zu verstehen.
Führt man den normierten Raum $V$ mit Hilfe einer Norm ein, so ist durch

\[d(x,y) = \|x-y\|\quad\text{für alle}\ x,y\in V\]

eine Metrik in $V$ gegeben.

Folgerung

Ein normierter Raum $(V, \|\cdot\|)$ ist ein linearer Raum, auf dem eine Norm $\|\cdot\|$ erklärt ist, die für alle $x,y\in V$ und $\alpha \in \mathbb{K}$

\[\begin{split}\begin{split} \|x\| & \ge 0,\quad \|x\|=0\quad \text{genau dann, wenn $x=0$ ist},\\ \|\alpha x\| & = |\alpha| \|x\|\\ \|x + y\| & \le \|x\| + \|y\|\end{split}\end{split}\]

erfüllt.

Damit können wir einen wichtigen Begriff der Funktionalanalysis einführen, den Banachraum:

Definition 3.17 (Banachraum)

Vollständig normierte Räume $V$ sind diejenigen, für die jede Cauchy-Folge in $V$ gegen ein Element in $V$ konvergiert.

Ein vollständiger normierter Raum heisst Banachraum.

Beispiele: Folgende Räume sind Banachräume

$\mathbb{R}^n$ mit der Norm $\|x\| = \sqrt{\sum_{k=1}^n |x_k|^2}$.
$C[a,b]$ mit der Norm $\|x\| := \max_{a\le t \le b} |x(t)|$.
$C^k[a,b]$ mit der Norm $\|x\| := \max_{a\le t \le b} |x(t)| + \max_{a\le t \le b} |x'(t)| + \ldots + \max_{a\le t \le b} |x^{(k)}(t)|.$
$l_p\ (1\le p < \infty)$ mit der Norm $\|x\| = \left(\sum_{k=1}^{\infty} |x_k|^p \right)^{1/p}$

Definition 3.18 (abzählbare Basis)

Man sagt, dass $V$ eine abzählbare Basis $\{x_k\}_{k=1}^{\infty}$ mit $x_k \in V$ besitzt, falls jedes $x\in V$ eindeutig in der Form $x = \sum_{k=1}^{\infty} \alpha_k\,x_k$ darstellbar ist, wobei die Konvergenz bezüglich der Norm von $V$ zu verstehen ist.

Lineare Räume können durchaus verschieden normiert werden. Als Beispiel betrachte dazu den Raum $V=\mathbb{R}^n$ mit den Normen

\[\begin{split}\begin{split} \|x\|_1 & = \sum_{k=1}^n |x_k|\quad\text{(Betragsnorm)}\\ \|x\|_2 & = \sqrt{\sum_{k=1}^n |x_k|^2}\quad\text{(Euklidische Norm, Quadratnorm)}\\ \|x\|_{\infty} & = \max_{1\le k \le n} |x_k|\quad\text{(Maximumsnorm)}\end{split}\end{split}\]

Aufgabe

Stelle den Einheitskreis $K_{*} = \{x\in\mathbb{R}^n\, \big|\, \|x\|_{*} = 1\}$ bezüglich den drei verschiedenen Normen $*$ graphisch dar.

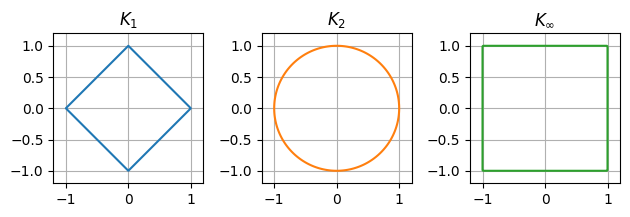
Die drei verschiedenen Normen führen zur Frage, wie die Normen zusammenhängen.

Defintion: äquivalente Normen

Im endlich dimensionalen gilt ein pauschaler Satz:

Satz 3.4

Alle Normen in einem endlich-dimensionalen Raum $V$ sind äquivalent.

Dieses Resultat gilt für unendlich-dimensionale Räume nicht. Als Beispiel sei der lineare Raum $C[a,b]$ mit der Maximumsnorm und der Quadratnorm erwähnt. Die beiden Normen sind nicht äquivalent, vgl. das Gegenbeispiel (3.3).

Mit diesem Satz folgt

Satz 3.5

Jeder endlich-dimensionale normierte Raum $V$ ist vollständig, also ein Banachraum.

3.3.2. Der Banachsche Fixpunktsatz#

Fixpunktsatz#

Abgesehen von den Beispielen folgt dieser Abschnitt [DR08].

Satz 3.6 (Fixpunktsatz)

Sei $X$ ein linear normierter Raum mit Norm $\|\cdot\|$. $E \subseteq X$ sei eine vollständige Teilmenge von $X$. Die Abbildung $\Phi$ sei eine Selbstabbildung auf $E$:

(3.4)#\[\Phi : E \to E.\]

Ferner sei $\Phi$ eine Kontraktion auf $E$:

(3.5)#\[\|\Phi(x) - \Phi(y)\| \le L \|x - y\| \quad \text{für alle } x, y \in E, \text{ mit } L < 1.\]

Dann gilt:

Es existiert genau ein Fixpunkt $x^*$ von $\Phi$ in $E$.
Für beliebiges $x_0 \in E$ konvergiert

\[ x_{k+1} = \Phi(x_k), \quad k = 0, 1, 2, \ldots \]

gegen den Fixpunkt $x^*$.
A-priori-Fehlerabschätzung:

(3.6)#\[ \|x_k - x^*\| \le \frac{L^k}{1 - L} \|x_1 - x_0\|.\]

A-posteriori-Fehlerabschätzung:

(3.7)#\[ \|x_k - x^*\| \le \frac{L}{1 - L} \|x_k - x_{k-1}\|.\]

Proof. Existenz

Zu beliebigem $x_0 \in E$ definiere $x_{k+1} = \Phi(x_k)$, $k = 0, 1, 2, \ldots$. Nach Voraussetzung (3.4) gilt $x_k \in E$ für alle $k$. Wegen (3.5) gilt

\[\begin{split} \begin{aligned} \|x_{k+1} - x_k\| &= \|\Phi(x_k) - \Phi(x_{k-1})\| \le L \|x_k - x_{k-1}\| \\ &\le L^k \|x_1 - x_0\| \quad \text{für alle } k. \end{aligned} \end{split}\]

Hiermit ergibt sich

\[\begin{split}\begin{aligned} \|x_{m+k} - x_k\| &= \|x_{m+k} \underbrace{- x_{m+k-1} + x_{m+k-1}}_{=0} + \ldots \underbrace{- x_{k+1} + x_{k+1}}_{=0} - x_k\| \\ &\le \underbrace{\|x_{m+k} - x_{m+k-1}\|}_{= (*)} + \ldots + \|x_{k+1} - x_k\|. \end{aligned}\end{split}\]

Für jeden Summanden folgt analog zu (*)

\[\begin{split}\begin{aligned} \|x_{m+k} - x_{m+k-1}\| & = \|\Phi(x_{m+k-1}) - \Phi(x_{m+k-2})\|\\ & \le L \|x_{m+k-1}-x_{m+k-2}\| \le \ldots \le L^{m+k-1} \|x_{1}-x_{0}\| \end{aligned}\end{split}\]

und damit

(3.8)#\[\begin{split}\begin{aligned} \|x_{m+k} - x_k\| &\le (L^{m+k-1} + \ldots + L^k) \|x_1 - x_0\| \\ &= L^k (L^{m-1} + \ldots + 1) \|x_1-x_0\|\\ &= L^k \frac{1 - L^m}{1 - L} \|x_1 - x_0\| \\ &\le \frac{L^k}{1 - L} \|x_1 - x_0\| \stackrel{k\to\infty}{\to} 0\,. \end{aligned}\end{split}\]

Wegen $L < 1$ folgt hieraus, dass $\{x_k\}_{k=0}^{\infty}$ eine Cauchy-Folge ist. Da $E$ vollständig ist, existiert also ein Grenzwert $x^*$, so dass

\[ \lim_{k \to \infty} x_k = x^* \,. \]

Für diesen Grenzwert gilt

\[\begin{split} \begin{aligned} x^* - \Phi(x^*) &= x^* - \Phi\bigl(\lim_{k \to \infty} x_k\bigr) = x^* - \lim_{k \to \infty} \Phi(x_k) \\ &= x^* - \lim_{k \to \infty} x_{k+1} = x^* - x^* = 0 \,, \end{aligned} \end{split}\]

und damit $x^* = \Phi(x^*)$, das heisst, $x^*$ ist Fixpunkt.

Eindeutigkeit

Seien $x^*$ und $x^{**}$ zwei verschiedene Fixpunkte so, dass $\Phi(x^*) = x^*$ und $\Phi(x^{**}) = x^{**}$ gilt. Dann folgt

\[ 0 < \|x^* - x^{**}\| = \|\Phi(x^*) - \Phi(x^{**})\| \le L \|x^* - x^{**}\| \quad \text{mit} \quad L < 1 \]

und damit der Widerspruch

\[\|x^* - x^{**}\| \le L \|x^* - x^{**}\| \quad \text{mit} \quad L < 1\]

beziehungsweise, da $\|x^* - x^{**}\|>0$

\[1 \le L \quad \text{mit} \quad L < 1.\]

Damit folgt $x^* = x^{**}$.

Fehlerabschätzungen

Zum Schluss werden die Fehlerabschätzungen abgeleitet. Nimmt man in (3.8) $m \to \infty$, ergibt sich das Resultat (3.6). Weiterhin gilt

\[\begin{split} \begin{aligned} \|x_k - x^*\| &\le \|x_k - x_{k+1}\| + \|x_{k+1} - x^*\| = \|x_{k+1} - x_k\| + \|\Phi(x_k) - \Phi(x^*)\| \\ &\le \|x_{k+1} - x_k\| + L \|x_k - x^*\| \,, \end{aligned} \end{split}\]

was die a-posteriori-Fehlerabschätzung (3.7) impliziert:

\[\begin{split} \begin{aligned} \|x_k - x^*\| & \le \frac{1}{1 - L} \|x_{k+1} - x_k\|\\ &= \frac{1}{1 - L} \|\Phi(x_{k}) - \Phi(x_{k-1})\|\\ \le \frac{L}{1 - L} \|x_k - x_{k-1}\| \,. \end{aligned}\end{split}\]

Korollar 3.1 (Folgerung)

Sei $X = \mathbb{R}^n$, $E \subseteq \mathbb{R}^n$ eine abgeschlossene konvexe Menge, und $\Phi : E \to \mathbb{R}^n$ sei stetig differenzierbar. Es gelte

\[ \Phi : E \to E \qquad \text{(Selbstabbildung)}, \]

und bzgl. einer Vektornorm $\|\cdot\|$ auf $\mathbb{R}^n$ gelte für die zugehörige Matrixnorm

\[ \max_{x \in E} \|\Phi'(x)\| = L < 1. \]

Dann sind alle Voraussetzungen aus dem Fixpunktsatz erfüllt.

Beispiele#

Beispiel 3.4

Ein einfaches Beispiel ist gegeben durch das Problem: Gesucht ist die Lösung der Fixpunktgleichung

\[x = \cos(x)\]

auf dem Intervall $[0,1]$. Wir betrachten daher die stetig differenzierbare Funktion

\[\begin{split}\begin{aligned} f : [0,1] & \to [0,1]\\ x & \mapsto f(x) = \cos(x). \end{aligned}\end{split}\]

Es gilt $f([0,1]) \subset [0,1]$ und $\max_{x\in[0,1]} |-\sin(x)| = \sin(1) < 1$. Damit sind die Voraussetzungen für den Satz Satz 3.6 erfüllt. Mit (3.6) können wir für einen Startwert $x_0 = 0.1$ die maximal erforderlichen Iterationsschritte abschätzen. Es gilt

\[k \le \frac{\log \left(\frac{(1-L) \text{tol}}{\|x_1-x_0\|}\right)}{\log (L)}\]

Typischerweise ist die Konvergenz besser.

../_images/9e85cda8a21d8c1e3a49011512c7f6f1b91e77726649f121ec22ceaf441d3ebc.png

Beispiel 3.5 (Fredholmsche Integralgleichung)

Gesucht ist eine stetige Funktion $u \in C([0,1])$ mit

(3.9)#\[u(x) = x + \frac{1}{2} \int_0^1 x\,t\,u(t)\,\mathrm{d}t, \qquad x \in [0,1].\]

Wahl des Raums. Sei $X = E = C([0,1])$ mit der Maximumnorm $\|u\|_\infty = \max_{x \in [0,1]} |u(x)|$. Dieser Raum ist vollständig.

Fixpunktform. Definiere $\Phi : C([0,1]) \to C([0,1])$ durch

\[ (\Phi u)(x) = x + \frac{1}{2} \int_0^1 x\,t\,u(t)\,\mathrm{d}t . \]

Dann ist (3.9) äquivalent zu $u = \Phi(u)$.

Selbstabbildung. Für $u \in C([0,1])$ ist $\Phi(u)$ wieder stetig, denn es ist $(\Phi u)(x) = x\left(1 + \tfrac{1}{2}\int_0^1 t\,u(t)\,\mathrm{d}t\right)$, also ein Vielfaches von $x$. Es gilt $\Phi : E \to E$.

Kontraktion. Für $u, v \in C([0,1])$ und $x \in [0,1]$ gilt

\[\begin{split} \begin{aligned} \|(\Phi u)(x) - (\Phi v)(x)\|_{\infty} &= \max_{x\in [0,1]} \left|\frac{1}{2}\, x \int_0^1 t\,\bigl(u(t) - v(t)\bigr)\,\mathrm{d}t \right| \\ &\le \frac{1}{2} \int_0^1 t\,\mathrm{d}t \;\|u - v\|_\infty = \frac{1}{4}\,\|u - v\|_\infty . \end{aligned} \end{split}\]

Somit gilt $\|\Phi(u) - \Phi(v)\|_\infty \le L\,\|u - v\|_\infty$ mit $L = \tfrac{1}{4} < 1$. Nach dem Satz 3.6 existiert genau eine Lösung $u^*$ in $C([0,1])$, und die Iteration $u_{k+1} = \Phi(u_k)$ konvergiert für jeden Startwert dagegen.

Iteration. Mit dem Startwert $u_0 = 0$ folgt $u_1(x) = x$, $u_2(x) = \frac{7}{6} x$, $u_3(x) = \frac{43}{36} x$. Allgemein folgt für die Fixpunktiteration

\[u_{k+1}(x) = \left(1+\frac{1}{2} \int_0^1 t\, u_k(t) dt \right) x = c_{k+1}\, x\]

jedes $u_k$ die Form $u_k(x) = c_k\,x$. Damit folgt

\[\left(1+\frac{1}{2} \int_0^1 t\, c_k\, t dt \right) x = c_{k+1}\, x\quad \forall\ x\in [0,1]\]

und somit

\[\left(1+\frac{1}{6} c_k\right) = c_{k+1}.\]

Für $k \to \infty$ gilt $c_k \to c$ und damit

\[\left(1+\frac{1}{6} c\right) = c\quad\Rightarrow\quad c = \frac{6}{5}.\]

Die exakte Lösung ist daher gegeben durch

\[ u^*(x) = \frac{6}{5}\,x . \]

Fehlerabschätzungen. Es gilt $\|u_1 - u_0\|_\infty = 1$ und $\|u_2 - u_1\|_\infty = \tfrac{1}{6}$. Für $k = 2$ erhält man:

a priori (3.6): $\|u_2 - u^*\|_\infty = \frac{1}{30} = 0.0\overline{3} \le \frac{L^2}{1-L}\,\|u_1 - u_0\|_\infty = \frac{1}{12} = 0.08\overline{3}$
a posteriori (3.7): $\|u_2 - u^*\|_\infty \frac{1}{30} = 0.0\overline{3} \le \frac{L}{1-L}\,\|u_2 - u_1\|_\infty = \frac{1}{18} = 0.0\overline{5}$

Beide Schranken sind gültig. Die a-posteriori-Schranke ist hier schärfer.

Die iterative Berechnung der Funktionen lässt sich mit sympy wie folgt umsetzen:

import sympy as sp

x,t = sp.symbols('x,t')

# Integral Operator
def F(u):
    return x + 1/2*sp.integrate(x*t*u(t),(t,0,1))

funcs = [0] # sp.exp(x)
for k in range(5):
    funcs += [F(sp.lambdify(x,funcs[-1],modules='sympy'))]
funcs

[0,
 x,
 1.16666666666667*x,
 1.19444444444445*x,
 1.19907407407408*x,
 1.19984567901235*x]

Sehr schnell sind die Beispiele nicht mehr als algebraischer Ausdruck integrierbar, weshalb numerische Methoden für die Berechnung einer Lösung benutzt werden müssen.