6. Variationsrechnung

Das Kapitel baut auf dem Buch [Kie10] auf.

Remark 6.1

Sämtliche Aussagen im Kapitel können auch für stückweise stetige oder stetig differenzierbare Funktionen gezeigt werden. Der Einfachheit schreiben wir jedoch nur \(C^0[a,b]\) bzw. \(C^1[a,b]\).

6.1. Einführendes Beispiel

Wir beginnen mit einem eindimensionalen Problem: gesucht ist \(u\in C^1(a,b)\) so, dass

\[J(u) = \int_a^b \left(\frac{1}{2} u'(x)^2 - f(x) u(x)\right) dx \to \min\]

gilt.

Wie in der Analysis reeller Funktionen soll für das Beispiel ein notwendiges Kriterium für eine Extremalstelle des Funktionals berechnet werden. Für die Herleitung gehen wir davon aus, dass \(u(x)\) ein Minimierer des Funktionals \(J\) ist. Diesen stören wir mit einer beliebigen Funktion \(v(x) \in C_0^\infty(a,b)\). Das bedeutet, dass \(v\) beliebig oft stetig differenzierbar ist und \(v(a) = v(b) = 0\) gilt. Wir betrachten daher \(J(u(x) + \varepsilon v(x))\). Falls \(u(x)\) eine Extremalstelle ist, so muss für alle \(v(x) \in C_0^\infty(a,b)\)

\[\frac{d}{d\varepsilon} J(u(x) + \varepsilon v(x))\big|_{\epsilon = 0} = 0\]

gelten.

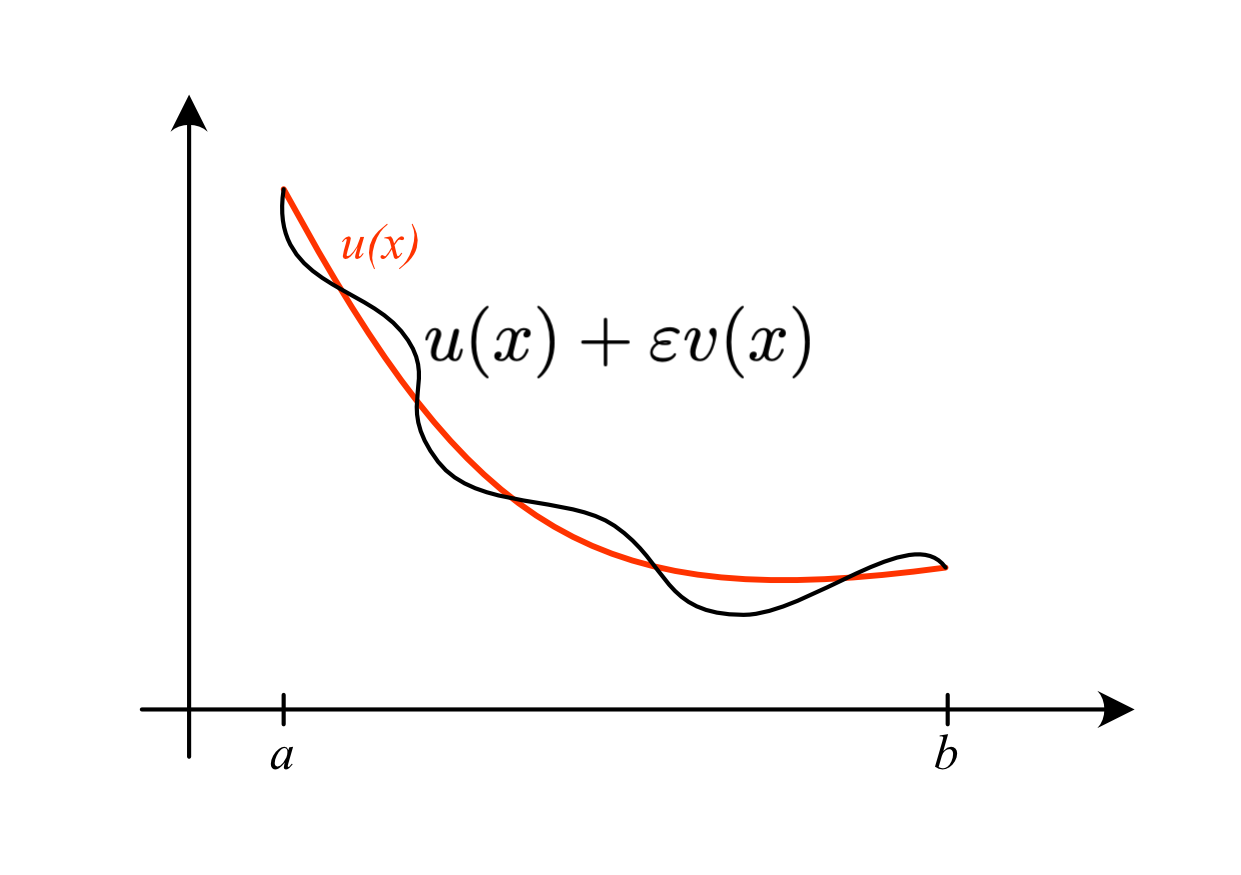
Abb. 6.1 Störung der Funktion \(u(x)\) durch \(\varepsilon v(x)\)

Wir berechnen daher

\[\begin{split}\begin{split} \frac{d}{d\varepsilon} J(u(x) + \varepsilon v(x))\big|_{\epsilon = 0} & = \frac{d}{d\varepsilon} \int_a^b \left( \frac{1}{2} (u'(x) + \varepsilon v'(x))^2 - f(x) (u(x) + \varepsilon v(x)) \right) dx \Big|_{\epsilon = 0}\\ & = \int_a^b \left((u'(x) + \varepsilon v'(x)) \cdot v'(x) - f(x) v(x)\right) dx \Big|_{\epsilon = 0}\\ & = \int_a^b \left(u'(x) \cdot v'(x) - f(x) v(x) \right) dx \end{split}\end{split}\]

Es folgt die schwache Gleichung

\[ \int_a^b \left(u'(x) \cdot v'(x) - f(x) v(x) \right) dx = 0\quad \forall v \in C_0^\infty(a,b).\]

Unter der Voraussetzung, dass \(u \in C^2(a,b)\) gilt, folgt mit Hilfe der partiellen Integration

\[ \underbrace{\left[ u'(x) v(x)\right]_a^b}_{=0\ \text{da}\ v(a)=v(b)=0} + \int_a^b \left(- u''(x) v(x) - f(x) v(x) \right) dx = 0\quad \forall v \in C_0^\infty(a,b).\]

und somit

\[ \int_a^b \left(- u''(x) - f(x)\right) v(x) dx = 0\quad \forall v \in C_0^\infty(a,b).\]

Der Fundamental-Lemma der Variationsrechnung besagt, dass die Gleichung nur dann erfüllt sein kann, wenn die starke Gleichung

\[- u''(x) - f(x) = 0\quad\text{oder}\quad - u''(x) = f(x)\]

gilt.

Theorem 6.1 (Fundamental-Lemma der Variationsrechnung)

Ist \(g\in C[a,b]\) und gilt

\[\int_a^b g(x) h(x) dx = 0\quad \text{für alle}\ h\in C_0^{\infty}(a,b),\]

so folgt \(g(x) = 0\) für alle \(x\in[a,b]\).

Wie aus dem Beispiel zu sehen ist, sind die Ansprüche an die Regularität in der starken Gleichung in der Regel grösser als die der schwachen Gleichung. Für skalare Funktionen ist das in der Regel kein grösseres Problem. Hingegen im Mehrdimensionalen führt dies zur Regularitätstheorie. Es muss studiert werden, wann eine schwache Lösung auch eine starke ist. Dies hängt im Mehrdimensionalen mit unter auch vom Gebiet \(\Omega \subset \mathbb{R}^n\) ab.

Im Beispiel sind ein paar Grundkonzepte enthalten, welche wir wie folgt festhalten

Definition 6.1 (Gâteaux-differenzierbar)

Sei \(X\) ein Banachraum. Existiert für \(J: X \to \mathbb{R}\) ein gegebenes Funktional

\[J'(\varepsilon=0) = \frac{d}{d\varepsilon} J(u + \varepsilon v)\big|_{\varepsilon = 0} = \lim_{\varepsilon \to 0} \frac{J(u + \varepsilon v) - J(u)}{\varepsilon},\]

so ist \(J\) in \(u\) in Richtung \(v\) Gâteaux-differenzierbar und die Ableitung wird als \(dJ(u,v)\) bezeichnet.

Das Gâteaux-Differential muss nicht zwingend linear noch stetig in \(v\) sein.

Definition 6.2 (Fréchet-Ableitung)

Existiert \(dJ(u,v)\) in \(u\in D \subset X\) für \(v\in X\) und ist \(dJ(u,v)\) linear in \(v\), so heisst \(dJ(u,v)\) die erste Variation oder Fréchet-Ableitung von \(J\) in Richtung \(v\). Wir schreiben in dem Fall

\[dJ(u,v) = \delta J(u) v = J'(u) v.\]

Ist dies für alle \(v\in D\subset X\) richtig, wobei \(D\) ein Unterraum von \(X\) ist, so ist

\[J'(u) : D \to \mathbb{R}\]

ein lineares Funktional.

Betrachten wir obiges Beispiel noch im mehrdimensionalen: gesucht ist \(u\in H_0^1(\Omega)\) so, dass

\[J(u) = \int_\Omega \left(\frac{1}{2} |\nabla u|^2 - f(x) u(x)\right) dx \to \min\]

gilt.

Wir berechnen die Gâteaux-Ableitung

\[\frac{d}{d\varepsilon} J(u + \varepsilon v)\big|_{\varepsilon = 0} = \int_\Omega \nabla u\cdot \nabla v - f v dx\]

Die Gâteaux-Ableitung ist linear in \(v\) und somit die erste Variation des Funktionals \(J : H_0^1(\Omega) \to \mathbb{R} \).

Mit der Forderung für einen Extremalpunkt \(J'(u) v = 0\) für alle \(v\in H_0^1(\Omega)\) haben wir die schwache Gleichung (vgl. Einleitung Poisson Gleichung (1.3))

\[\int_\Omega \nabla u\cdot\nabla v dx = \int f(x) v dx \quad \forall v \in H_0^1(\Omega).\]

Mit Hilfe des Gauss-Theorem oder partiellen Integration im mehrdimensionalen folgt die starke Gleichung (partielle Differentialgleichung)

\[-\Delta u = f(x)\quad x\in\Omega\]

mit der Dirichlet Randbedingung \(u(x) = 0\) auf dem Rand \(\partial\Omega\).

Bemerkung

Halten wir fest: Durch Testen der partiellen Differentialgleichung erhalten wir die schwache Gleichung, welche dem notwendigen Kriterium (Fréchet-Ableitung ist Null) eines zu (typischerweise) minimierenden Funktionals entspricht.

6.2. Euler-Lagrange Gleichung

Für die Herleitung der formalen Euler-Lagrange Gleichung beschränkten wir uns auf eindimensionale Probleme. Wir betrachten das zu minimierende Funktional

(6.1)\[J(u) = \int_a^b F(x,u,u') dx,\]

welches auf \(C^1(a,b)\) definiert ist.

Definition 6.3 (lokaler Minimierer)

Sei \(X\) ein Banachraum. Eine Funktion \(u\in X\) heisst lokaler Minimierere für das Funktional \(J : X \to \mathbb{R}\), falls

\[J(u) \le J(v)\quad\text{für alle}\ v\in X\ \text{mit}\ \|u-v\|_X < \delta\]

mit einer Konstante \(\delta > 0\) gilt.

Analog wird ein lokaler Maximierer definiert. Man beschränkt sich in der Regel auf Minimierer und betrachtet für Maximierer das Funktional \(-J\).

Wir betrachten nun das Funktional (6.1) und berechnen die Gâteaux-Ableitung für beliebiges \(v\in C_0^\infty(a,b)\)

\[\begin{split}\begin{split} \frac{d}{d\varepsilon} J(u+\varepsilon v)\big|_{\varepsilon=0} & = \frac{d}{d\varepsilon} \int_a^b F(x,u+\varepsilon v,u'+\varepsilon v') dx \Big|_{\varepsilon=0}\\ & = \int_a^b \left(\partial_{u} F(x,u,u')\cdot v + \partial_{u'} F(x,u,u')\cdot v' \right) dx \end{split}\end{split}\]

Partielle Integration des zweiten Summanden liefert

\[J'(u) v = \int_a^b \left(\partial_{u} F(x,u,u')\cdot v - \frac{d}{dx} \partial_{u'} F(x,u,u')\cdot v\right) dx + \left[ \partial_{u'} F(x,u,u')\cdot v \right]_a^b.\]

Da \(v\in C_0^\infty(a,b)\) folgt \(v(a) = v(b) = 0\) und damit

\[J'(u) v = \int_a^b \left(\partial_{u} F(x,u,u') - \frac{d}{dx} \partial_{u'} F(x,u,u')\right)\cdot v dx.\]

Wir können damit folgenden Satz festhalten:

Theorem 6.2

Die Funktion \(u\in C^1(a,b)\) sei ein lokaler Minimierer für das Funktional (6.1) und die Lagrange-Funktion \(F: [a,b] \times \mathbb{R} \times \mathbb{R}\) sei stetig und bezüglich der letzten beiden Variablen stetig partiell differenzierbar. Dann gilt die Euler-Lagrange-Gleichung

(6.2)\[\frac{d}{dx} \partial_{u'} F(x,u,u') = \partial_{u} F(x,u,u').\]

Remark 6.2

• Wir haben den Satz für stetige Funktionen auf ganz \([a,b]\) notiert. Das Resultat lässt sich auf stückweise stetige Funktionen verallgemeinern.

• Im hier notierten Fall von Funktionen in einer Variablen \(x\) gilt, dass eine Lösung der schwachen Gleichung

  \[\int_a^b \left(\partial_{u} F(x,u,u')\cdot v + \partial_{u'} F(x,u,u')\cdot v' \right) dx = 0\quad \forall\ v\in C_0^\infty(a,b)\]

  auch Lösung der starken Gleichung (6.2) ist.

• Ist die Lagrange-Funktion nicht explizit von \(x\) abhängig, können wir die Lagrange-Gleichung umformen - vorausgesetzt die Regularität von \(u\) erlaubt ein zweimaliges Ableiten.

  Es gilt

  \[\begin{split}\begin{split} \frac{d}{dx} (F - u' F_{u'}) & = F_u u' + F_{u'} u'' - u'' F_{u'} - u' \frac{d}{dx} F_{u'}\\ & = \underbrace{\left(F_u - \frac{d}{dx} F_{u'}\right)}_{=0\, (*)} \cdot \underbrace{u'}_{=0\, (**)} = 0\quad \text{für}\, x\in [a,b].\end{split}\end{split}\]

  Daraus folgt, dass jede Lösung der Euler-Lagrange-Gleichung \((*)\) und jede Konstante \((**)\) ebenfalls Lösung der Differentialgleichung erster Ordnung

  (6.3)\[F(u,u') - u' F_{u'}(u,u') = c_1\quad\text{für}\, x\in [a,b]\]

  ist.

6.3. Beispiele zur Lösung der Euler-Lagrange-Gleichung

6.3.1. Kürzeste Verbindung zweier Punkte

Wir betrachten in der Ebene zwei Punkte \((a,A), (b,B)\) und suchen nach der kürzesten Kurve, welche diese verbindet. Beschreibt man die Kurve mit einer Funktion \(y: [a,b] \to \mathbb{R}\), so können wir die Länge mit dem Funktional

\[J(y) = \int_{a}^{b} \sqrt{1+y'(x)^2} dx\]

berechnen. Gesucht ist daher ein Minimierer des Funktionals \(J(y)\). Die zugehörige Euler-Lagrange Gleichung lautet

\[\frac{d}{dx} \frac{y'(x)}{\sqrt{1+y'(x)^2}} = 0.\]

Integration liefert

\[\frac{y'(x)}{\sqrt{1+y'(x)^2}} = a.\]

Durch auflösen nach \(y'\) und integrieren erhalten wir den Kanditaten für einen Minimierer

\[y(x) = \frac{a}{\sqrt{1-a^2}} x + b = m\, x + b,\]

also eine Gerade zwischen den beiden Punkten. Die beiden Integrationskonstanten können aus den Randbedingungen \(y(a) = A\) und \(y(b) = B\) bestimmt werden. Es stellt sich natürlich die Frage, ist die Lösung ein Minimierer und falls ja ein globaler?

Analog zur Analysis reeller Funktionen kann auf für Funktionale unter geeigneten Voraussetzungen ein Kriterium, die zweite Variation, berechnet werden. Es gilt der Satz

Theorem 6.3

Sei die Lagrange-Funktion (6.1) zweimal bezüglich den letzten beiden Variablen stetig partiell differenzierbar. Dann ist die zweite Variateion oder zweite Fréchet-Ableitung gegeben durch die Bilinearform

\[\begin{split}\begin{split}\delta^2 J(u)(v,w) = \int_a^b \Big[ & \Big(\partial_{u,u}F(x,u,u') - \frac{d}{dx} \partial_{u',u}F(x,u,u')\Big) v w\\ & + \partial_{u',u'}F(x,u,u') v' w' \Big] dx\end{split}\end{split}\]

Für einen lokalen Minimierer \(u\) gilt neben der notwendigen Bedingung \(J'(u) v = 0\) die hinreichende Bedingung von Legendre

\[\partial_{u',u'} F(x,u,u') \ge 0\quad \forall\ x\in [a,b].\]

Gilt für alle \(w \in D\subset C^1(a,b) \cap \{w(a)=A, w(b)=B\}\)

\[\delta^2 J(w)(v,v) \ge 0\quad \forall\ v \in C_0^\infty(a,b),\]

so ist \(u\) ein globaler Minimierer von \(J\) auf \(D\).

Der Satz auf das Beispiel angewandt zeigt uns, dass wir globalen Minimierer gefunden haben.

6.3.2. Das Problem von Johann Bernoulli

Das original Problem wurde wie folgt beschrieben:

Wenn in einer vertikalen Ebene zwei Punkte A und B gegeben sind, soll man dem beweglichen Punkt M eine Bahn AMB anweisen, auf welcher er von A ausgehend vermöge seiner eigenen Schwere in kürzester Zeit nach B gelangt.

Der Punkt \(B\) liegt trivialerweise unterhalb von \(A\). Entsprechend wählen wir ein passendes Koordinatensystem gemäss Abb. 6.2.

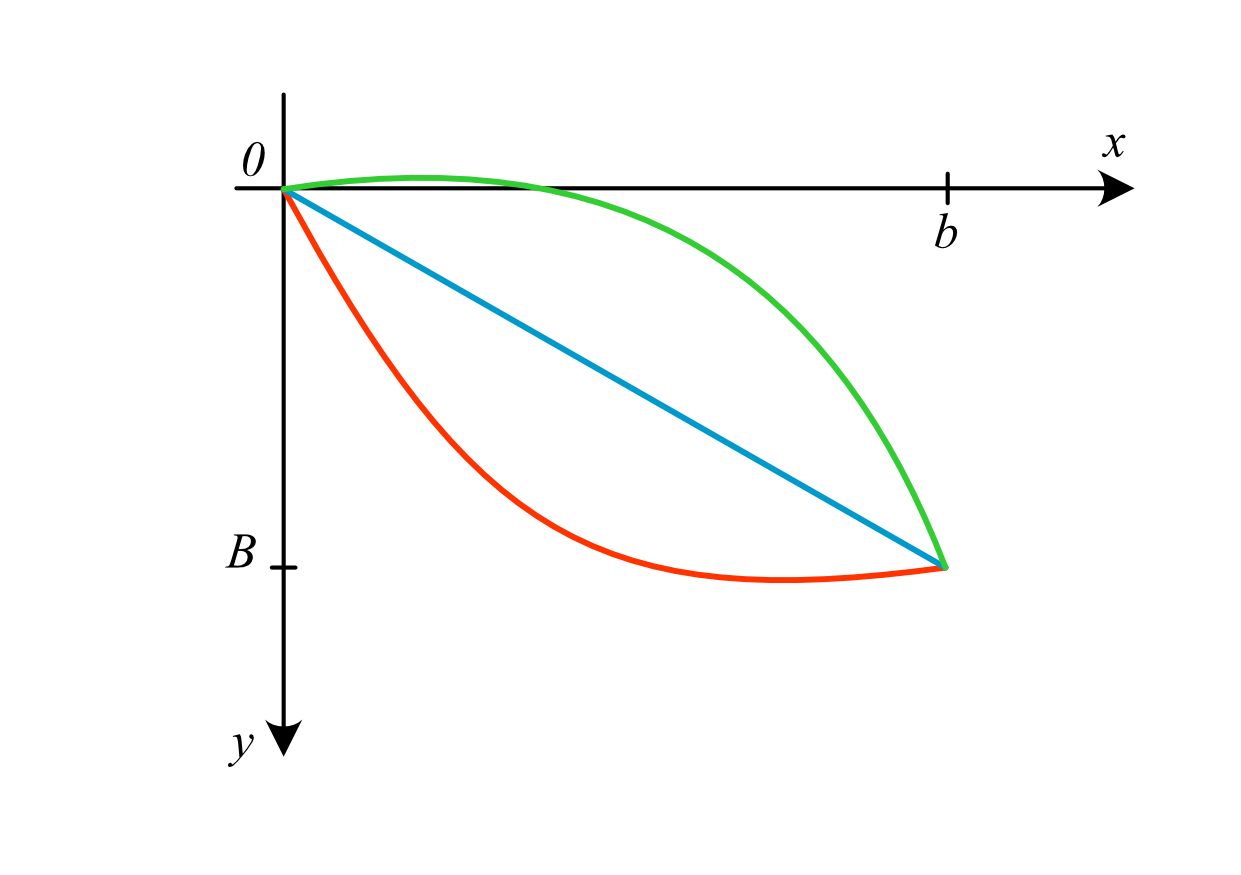
Abb. 6.2 Gesucht ist die schnellste Bahn.

Wir parametrieren die Bahnkurve nach der Zeit \(t\): \(\{(x(t),y(t)\,|\, t \in [0,T])\}\). Dabei gilt \((x(0),y(0)) = (0,0)\) und \((x(T),y(t)) = (b,B)\). Die Laufzeit ist gegeben durch \(T\). Nach dem Energieerhaltungsgesetz ist die Summe der kinetischen und potentiellen Energie längs der Bahn konstant

\[\frac{1}{2} m v^2 + m g (h_0-y) \equiv m g h_0.\]

Die Masse \(m\) ist offensichtlich nicht relevant. Mit \(h_0\) sei die Höhe zwischen \(A\) und \(B\) bezeichnet und mit \(g\) die Erdbeschleunigung. Für die Geschwindigkeit erhalten wir

\[v(t) = \sqrt{2 g y(t)}.\]

Andererseits folgt aus dem parametrischen Ansatz für die Geschwindigkeit

\[v(t) = \sqrt{\dot{x}(t)^2+\dot{y}(t)^2} = \sqrt{1 + \left(\frac{dy}{dt} \frac{dt}{dx}\right)^2}\cdot \dot{x}(t) = \sqrt{1 + y'(x(t))^2}\cdot \dot{x}(t)\]

Es gilt daher

\[\frac{\sqrt{1 + y'(x(t))^2}\cdot \dot{x}(t)}{\sqrt{2 g y(x(t))}} \equiv 1 \quad \forall t\in [0,T].\]

Wir nutzen diese Identität um die Laufzeit zu berechnen

\[T = \int_0^T 1 dt = \int_0^T \sqrt{\frac{1 + y'(x(t))^2}{2 g y(x(t))}} \cdot \dot{x}(t) dt\]

Mit der Transformation \(x=x(t)\) folgt \(dx = \dot{x}(t) dt\) und damit für das Integral

\[T = \int_0^b \sqrt{\frac{1 + y'(x)^2}{2 g y(x)}} dx.\]

Für das zu minimierende Funktional erhalten wir

(6.4)\[J(y) = \int_0^b \sqrt{\frac{1 + y'(x)^2}{y(x)}} dx,\]

wobei wir den Faktor \(1/\sqrt{2g}\) weglassen, da das Resultat unabhängig davon ist. Die Graphitation beeinflusst die Kurvenform nicht.

Der Integrand des Funktional (6.4) ist für \(x=0\) unbestimmt, einerseits kann aus physikalischen Gründen \(y'(0) = +\infty\) sein und andererseits gilt \(y(0) = 0\). Das Integral ist daher als uneigentliches Integral zu verstehen. Zu dem ist \(J\) nur auf \((0,b]\) positive Funktionen \(y(x)\) definiert. Deshalb legen wir die zulässigen Funktionen wie folgt fest:

\[\begin{split}\begin{split} D = C[0,b] & \cap C^1(0,b] \cap \{y(0) = 0, y(b) = B\}\\ & \cap \{y > 0\, \text{in}\ (0,b]\} \cap \{J(y) < \infty\}.\end{split}\end{split}\]

Die Lagrange-Funktion hat im Beispiel die spezielle Eigenschaft, dass sie nicht explizit von \(x\) abhängig ist. Daher benutzen wir die Form (6.3), womit die Differentialgleichung

(6.5)\[y'(x) = \frac{\sqrt{2r- y(x)}}{\sqrt{y(x)}}\quad \text{mit}\ 2r = \frac{1}{c_1^2}>0\]

folgt. Die Differentialgleichung kann in dieser Form nicht geschlossen gelöst werden. Daher wechseln wir wieder in die parametrische Form

\[(x,y(x)) = (\hat{x}(s), \hat{y}(s)),\quad x\in[0,b],\ s \in [s_0,s_b],\]

wobei \(s\) nicht die physikalische Zeit ist. Es gilt

\[\hat{y}(s) = y(\hat{x}(s)),\quad \frac{dy}{ds}(s) = y'(\hat{x}(s)) \frac{d\hat{x}}{ds}(s).\]

Die Differentialgleichung (6.5) eingesetzt liefert

\[\frac{d\hat{x}}{ds}(s) = \frac{d\hat{y}}{ds}(s) \frac{1}{y'(\hat{x}(s))} = \frac{d\hat{y}}{ds}(s) \sqrt{\frac{\hat{y}(s)}{2r-\hat{y}(s)}}.\]

Es kann gezeigt werden, dass

\[\begin{split}\begin{split} \hat{x}(s) & = r\cdot (s - \sin(s))\\ \hat{y}(s) & = r\cdot (1 - \cos(s))\end{split}\end{split}\]

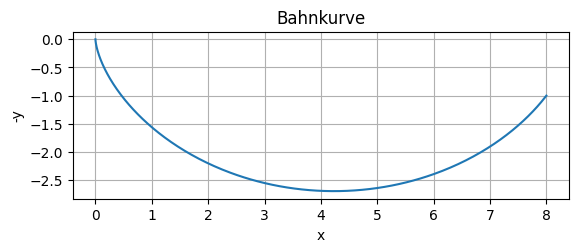
für \(s\in [0,s_b]\) Lösung und damit Lösungskurve der Aufgabe ist. Die Bahnkurve wird Brachystochrone genannt und durch eine Zykloide beschrieben. Der Parameter \(r\) ist gegeben durch

\[r = \frac{B}{1-\cos(s_b)}\]

und \(s_b\) ist implizit gegeben durch die Gleichung

\[\frac{b}{B} = \frac{s_b-\sin(s_b)}{1-\cos(s_b)} =: f(s_b).\]

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import fsolve
from myst_nb import glue

f = lambda sb : (sb - np.sin(sb))/(1-np.cos(sb))

b=8
B=1
glue("b_example", b, display=False)
glue("B_example", B, display=False)

sb = fsolve(lambda s: f(s)-b/B,5)[0]
r = B/(1-np.cos(sb))
glue("sb_example", np.round(sb,4), display=False)
glue("r_example", np.round(r,4), display=False)

sbi = np.linspace(1e-3,2*3.14,400)
plt.plot(sbi, f(sbi),label='$f(s_b)$')
plt.legend()
plt.axvline(np.pi,c='gray')
plt.axhline(np.pi/2,c='gray')
plt.grid()
plt.ylim(0,10)
plt.title('$f(s_b)$ ist monoton wachsend')
plt.xlabel('$s_b$')   
plt.ylabel('$b/B$')
plt.show()

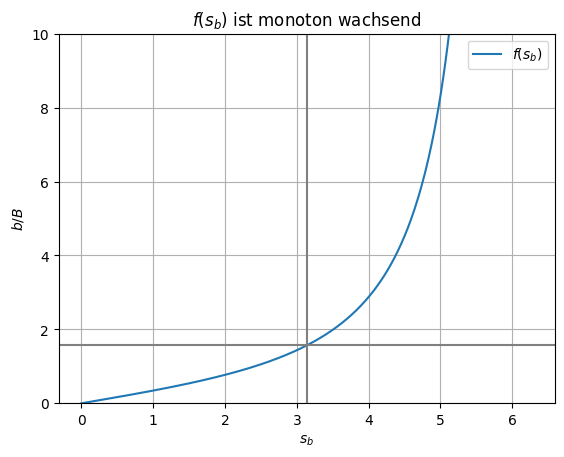
Die Funktion \(f(s_b)\) ist monoton wachsend. Für \(b/B \ge \pi/2\) gilt \(s_b \in [\pi, 2\pi]\). Das bedeutet, dass das Minimum der Bahnkurve tiefer als der Punkt \(B\) liegt. Für \(b = \) 8 und \(B = \) 1 folgt \(s_b =\) np.float64(4.9729) und \(r = \) np.float64(1.347). Damit können wir die Bahnkurve visualisieren:

Show code cell source Hide code cell source

si = np.linspace(0,sb,400)

plt.plot(r*(si-np.sin(si)),-r*(1-np.cos(si)))
plt.grid()
plt.gca().set_aspect(1)
plt.xlabel('x')
plt.ylabel('-y')
plt.title('Bahnkurve')
plt.show()