9.1. Finite Elemente Methode Einstiegsbeispiele#
9.1.1. Eindimensionaler Fall#
Zum Einstieg in die Methode der finite Elemente kommen wir auf das skalare Randwertproblem (1.1), dem Poisson Problem zurück
mit \(f(x) = 1\).
Die analytische Lösung erhalten wir in dem Fall leicht. Durch zweimaliges Integrieren der rechten Seite erhalten wir ein Polynom 2. Grades
Durch Einsetzen der Randbedingungen folgt die analytische Lösung
def uanalytic(x):
return -0.5*x*(x-1)
Für die numerische Lösung multiplitzieren wir die Differentialgleichung mit einer beliebigen Testfunktion \(v(x)\in C_0^\infty(0,1)\) und integrieren über das Intervall \((0,1)\)
Mit Hilfe der partiellen Integration erhalten wir die schwache Gleichung
Gesucht ist eine Funktion \(u(x)\) so, dass \(u(0)=u(1)=0\) und
Um der Gleichung zu genügen, muss die Lösung \(u\) nicht zwingend eine zweimal stetig differenzierbare Funktion sein. Anstelle dessen werden \(u\) und \(v\) jeweils einmal differenziert. Die Funktionen liegen im Sobolev-Raum \(H_0^1(0,1)\). Die rechte Seite muss ebenfalls nicht mehr zwingend stetig sein. Es reicht, wenn die Funktion \(f\) quadratisch integrierbar ist, daher \(f\in L_2(0,1)\). Die finite Elemente Methode benutzt die eingeführte verallgemeinerte Ableitung (5.1). Wir erhalten Lösungen, welche nicht immer zwingend auch Lösung der starken Gleichung (9.1) sein müssen.
Wir diskretisieren nun das Intervall \((0,1)\) in Teilintervalle \((x_{i-1},x_i)\) für \(i=1,\ldots, n\). Auf dieser Zerlegung definieren wir die Basisfunktionen
mit welchen wir den Sobolevraum \(H_0^1(0,1)\) approximieren.
Direkte (numpy) Lösung#
Show code cell content
import numpy as np
import matplotlib.pyplot as plt
from myst_nb import glue
n=5
a=0
b=1
xi = np.linspace(a,b,n+1)
def phi(i,x,xi=xi):
"""
1d affine FEM Basisfunktionen
Parameters
----------
i : int, Nummer der Basisfunktion
x : nparray, Koordinaten für Auswertung
xi : nparray, Knoten
Return
------
y : nparray, Funktionswerte für x
"""
y = np.zeros_like(x)
if i > 0:
ind = (xi[i-1]<=x)*(x<=xi[i])
y[ind] = (x[ind]-xi[i-1])/(xi[i]-xi[i-1])
if i < n:
ind = (xi[i]<=x)*(x<xi[i+1])
y[ind] = (xi[i+1]-x[ind])/(xi[i+1]-xi[i])
return y
xp = np.linspace(a,b,400)
fig, ax = plt.subplots(figsize=(6, 2))
for i in range(n+1):
ax.plot(xp,phi(i,xp),label=r'$\varphi_'+str(i)+'$')
ax.legend(loc='upper right', bbox_to_anchor=(1.2, 1))
glue("FEM_1d_p1_fig", fig, display=False)
glue("FEM_1d_p1_n",n,display=False)
In der Abbildung Abb. 9.1 ist das Intervall in 5 Teilintervalle zerlegt. Entsprechend haben wir 5 +1 Basisfunktionen. Abgesehen von der ersten und letzten Basisfunktion erstreckt sich der Support jeweilen über zwei Teilintervalle. Die Basisfunktionen sind genau in einem Knoten \(x_i\) eins, in allen anderen beträgt der Funktionswert 0.
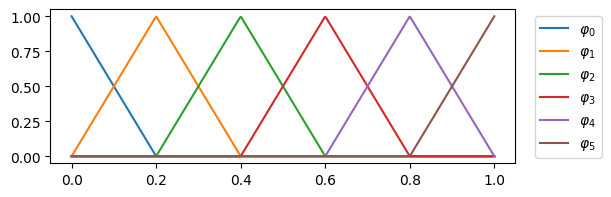
Abb. 9.1 FEM 1d affine Basisfunktionen#
Für die schwache Gleichung (9.2) erhalten wir das endlich dimensionale mit finite Elemente diskrete Problem
Gesucht ist eine Funktion
so, dass \(u(0) = u(1) = 0\) und
Setzt man die Darstellung für \(u_h\) ein, so folgt
Wir definieren die Matrix \(A\) und den Vektor \(b\)
und erhalten so das (reduzierte) lineare Gleichungssystem für die Koeffizienten \(u_1, \ldots, u_{n-1}\)
Um die Matrix \(A\) aufzustellen werden die Ableitungen der Basisfunktionen \(\varphi_i\) benötigt. Gehen wir wie im Beispiel oben Abb. 9.1 von einer konstanten Unterteilung aus, so gilt
Show code cell content
def dphi(i,x,xi=xi):
"""
Ableitung 1d affine FEM Basisfunktionen
Parameters
----------
i : int, Nummer der Basisfunktion
x : nparray, Koordinaten für Auswertung
xi : nparray, Knoten
Return
------
y : nparray, Funktionswerte für x
"""
y = np.zeros_like(x)
if i > 0:
h = xi[i]-xi[i-1]
ind = (xi[i-1]<=x)*(x<=xi[i])
y[ind] = np.ones_like(x[ind])/h
if i < n:
h = xi[i+1]-xi[i]
ind = (xi[i]<=x)*(x<xi[i+1])
y[ind] = -np.ones_like(x[ind])/h
return y
fig, ax = plt.subplots(figsize=(6, 2))
for i in range(n+1):
ax.plot(xp,dphi(i,xp),label=r'$\varphi_'+str(i)+'\'(x)$')
ax.legend(loc='upper right', bbox_to_anchor=(1.25, 1.05))
glue("FEM_1d_p1_deriv_fig", fig, display=False)
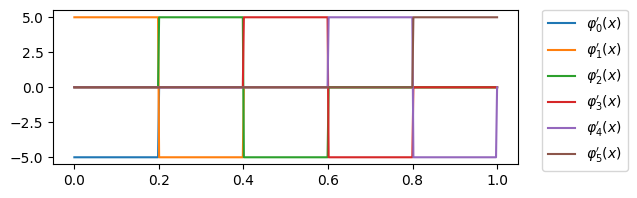
Abb. 9.2 Ableitung FEM 1d affine Basisfunktionen#
Für das konkrete Beispiel erhalten wir für die Matrixkoeffizienten die Matrix \(A\):
Show code cell source
from scipy.integrate import fixed_quad
A = []
for i in range(0,n+1):
ai = []
for j in range(0,n+1):
# Integration über die Elemente mit Hilfe der Gauss-Quadratur
aij = np.sum([fixed_quad(lambda x:dphi(i,np.array(x))*dphi(j,np.array(x)), xi[k], xi[k+1],n=2)[0]
for k in range(n)])
ai.append(aij)
A.append(ai)
A = np.array(A,dtype=float)
A
array([[ 5., -5., 0., 0., 0., 0.],
[-5., 10., -5., 0., 0., 0.],
[ 0., -5., 10., -5., 0., 0.],
[ 0., 0., -5., 10., -5., 0.],
[ 0., 0., 0., -5., 10., -5.],
[ 0., 0., 0., 0., -5., 5.]])
Aufgabe
Berechne die Koeffizienten von Hand.
Analog zur Matrix \(A\) folgt für die rechte Seite mit konkreter Funktion \(f(x) = 1\):
Show code cell source
def f(x):
x = np.array(x)
return np.ones_like(x)
b = []
for j in range(0,n+1):
b.append(np.sum([fixed_quad(lambda x:f(np.array(x))*phi(j,np.array(x)),
xi[k], xi[k+1],n=2)[0]
for k in range(n)]))
b = np.array(b,dtype=float)
b
array([0.1, 0.2, 0.2, 0.2, 0.2, 0.1])
Die FEM Lösung \(u(x)\) ist somit gegeben durch die Lösung des Gleichungssystems (9.5) mit der berechneten Matrix und Vektor. Da die Randwerte gegeben sind, werden nur die inneren Freiheitsgrade benutzt. Es folgt
u = np.zeros_like(xi)
# um die Wahl der linearen Gleichungslöser kümmern wir uns später:
u[1:-1] = np.linalg.solve(A[1:-1,1:-1],b[1:-1])
u
array([0. , 0.08, 0.12, 0.12, 0.08, 0. ])
Show code cell content
xp = np.linspace(0,1,400)
fig, ax = plt.subplots(figsize=(6, 2))
ax.plot(xi,u,label='FEM Lösung')
ax.plot(xp,uanalytic(xp),label='exakte Lösung')
ax.legend()
glue("FEM_1d_p1_solutionexmp_fig", fig, display=False)
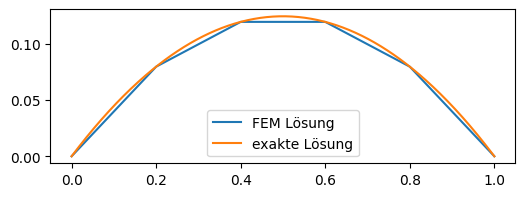
Abb. 9.3 Lösung des Randwertproblem mit Hilfe 1. Ordnung FEM#
Aufgaben
Wie lautet das Gleichungssystem, wenn für die Integration der rechten Seite die Trapezregel benutzt wird?
Berechne die Lösung mit Hilfe der finiten Differenzen Methode und vergleiche die beiden Systeme.
NGSolve Lösung#
Das selbe nun mit NGSolve
Wir erstellen als erstes ein eindimensionales Mesh.
from netgen.meshing import Mesh as NGMesh # Vorsicht es gibt Mesh auch in ngsolve!
from netgen.meshing import MeshPoint, Pnt, Element1D, Element0D
from ngsolve import *
m = NGMesh(dim=1)
# Anzahl Teilintervalle
N = 5
# Punkte für die Zerlegung auf dem Intervall [0,1]
pnums = []
for i in range(0, N+1):
pnums.append (m.Add (MeshPoint (Pnt(i/N, 0, 0))))
# Jedes 1D-Element (Teilintervall) kann einem Material zugeordnet
# werden. In unserem Fall gibt es nur ein Material.
idx = m.AddRegion("material", dim=1)
for i in range(0,N):
m.Add (Element1D ([pnums[i],pnums[i+1]], index=idx))
# Linkes und Rechtes Ende sind Randwertpunkte (0D-Elemente)
idx_left = m.AddRegion("left", dim=0)
idx_right = m.AddRegion("right", dim=0)
m.Add (Element0D (pnums[0], index=idx_left))
m.Add (Element0D (pnums[N], index=idx_right))
# Damit haben wir das Mesh definiert
mesh = Mesh(m)
Nun erstellen wir einen \(H^1\) Funktionenraum mit Hilfe dieses 1D Mesh und den Dirichlet Randpunkte left und right.
V = H1(mesh,order = 1, dirichlet='left|right')
u = V.TrialFunction()
v = V.TestFunction()
# abgekürzt
# u,v = V.TnT()
\(u,v\) sind Trial und Test Funktionen für die Definition der Linear- und Bilinearfunktion
a = BilinearForm(V)
a += grad(u)*grad(v)*dx
f = CoefficientFunction(1)
b = LinearForm(V)
b += f*v*dx
Damit sind die beiden Operatoren definiert, jedoch noch nicht berechnet. Das Berechnen nennt man auch assembling Zusammenstellen. Wir werden später sehen, was damit gemeint ist.
a.Assemble()
b.Assemble();
Die Matrix und der Vektor der Bilinear- und Linearform beinhaltet sämtliche Freiheitsgrade, insbesondere also auch die Randpunkte. Diese sind jedoch durch die Dirichletrandwerte gegeben und müssen nicht berechnet werden. Dem werden wir beim Lösen des Systems rechnungtragen.
print(a.mat)
Row 0: 0: 5 1: -5
Row 1: 0: -5 1: 10 2: -5
Row 2: 1: -5 2: 10 3: -5
Row 3: 2: -5 3: 10 4: -5
Row 4: 3: -5 4: 10 5: -5
Row 5: 4: -5 5: 5
print(b.vec)
0.1
0.2
0.2
0.2
0.2
0.1
Die Lösung selber wird in einer GridFunction gespeichert. Die Trial und Test Functions haben zwar die gleiche Struktur, jedoch keinen Memory. Hier sind nur die Freiheitsgrade etc. des FE-Raumes gespeichert. Für die Lösung benötigen wir eine GridFunction. In der Auswertung dieser wird Linearkombination der Basisfunktionen automatisch berechnet.
gfu = GridFunction(V)
Berechnung der FEM Lösung mit NGSolve:
gfu.vec.data = a.mat.Inverse(freedofs=V.FreeDofs())*b.vec
Bei der Ausführung des Befehls wird nicht die Matrix Invertiert und von links an den Vektor multipliziert. Das wäre numerisch viel zu aufwändig. Auch wenn die Notation anderes behauptet, es wird nur das Gleichungssystem gelöst.
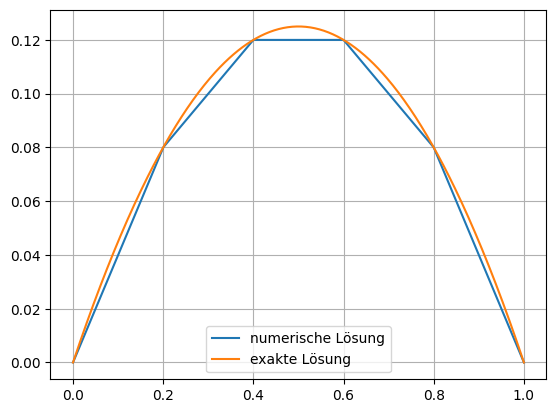
Es folgt das selbe Resultat wie oben:
Show code cell source
xp = np.linspace(0,1,400)
plt.plot(xp,[gfu(mesh(xi,0)) for xi in xp],label='numerische Lösung')
plt.plot(xp, uanalytic(xp),label='exakte Lösung')
plt.legend()
plt.grid()
plt.show()
9.1.2. Zweidimensionaler Fall#
Wir betrachten nun das Beispiel Randwertproblem
auf dem einheits Rechteck im \(\mathbb{R}^2\). Analog zum Einstiegsbeispiel Abschnitt 1.1.2 folgt die schwache Gleichung
wobei mit \(J\) die Basisfunktionen bezeichnet sind, deren Maximum im Innern des Einheitsquadrats angenommen werden.
from ngsolve import *
from ngsolve.webgui import Draw
Von netgen importieren wir das Einheits Quadrat. Mit Hilfe des netgen Moduls können wir 2d und 3d Geometrien definieren und vernetzen.
from netgen.geom2d import unit_square
Wir generieren nun unstrukturiertes Mesh mit der maximalen Kantenlänge von 0.25:
mesh = Mesh(unit_square.GenerateMesh(maxh=0.25))
Damit erhalten wir das Mesh, wobei die Feinheit über den maxh Parameter gesteuert werden kann.
Draw(mesh);
Wie sehen im zweidimensionalen die Basisfunktionen aus? Dazu erstellen wir einen FEM Funktionenraum und visualisieren die Basisfunktionen. Der Rand des Einheitsquadrats besteht aus 4 Linien, welche verschiedene Labels haben:
mesh.GetBoundaries()
('bottom', 'right', 'top', 'left')
Wir definieren den H1 FEM Funktionenraum mit der Dirichletrandbedingung und initialisieren eine GridFunction, eine FEM Funktion aus dem Funktionenraum:
V = H1(mesh,order=1,dirichlet='bottom|right|top|left')
gfu = GridFunction(V)
In der Gridfunction wird der Lösungsvektor, die Koeffizienten der Linearkombination der Basisfunktionen gespeichert. In diesen Vektor schreiben wir nun an unterschiedlichen Stellen eine 1, womit wir die verschiedenen Basisfunktionen visualisieren können.
gfu.vec.FV()[:] = 0 # alle Einträge mit 0 initialisieren
gfu.vec.FV()[20] = 1
Draw(gfu,mesh,'u');
Die inneren Freiheitsgrade sind in unserem Fall die freien Freiheitsgrade des FEM Raumes, daher in der Zahl 9 Stück:
freedofs = V.FreeDofs()
print (freedofs)
freedofsnp = np.array([i for i in freedofs])
0: 00000000000000001111111111
Wir setzen nun alle inneren Freiheitsgrade auf 1 und erhalten damit die Linearkombination der Basisfunktionen:
gfu.vec.FV().NumPy()[freedofsnp] = 1.
Draw(gfu);
Die Ableitungen der Basisfunktionen sind stückweise konstante Funktionen. Überschlagen wir hier kurz die Steigung: \(1/4\)-tel ist die Seitenlänge der Zerlegung. Das bedeutet, dass die Steigung in \(x/y\) Richtung 4 beträgt.
Visualisieren wir von \(\nabla u\) die \(x\)-Komponente, so sollte, das einen Graph mit stückweise \(\pm 4\) in den Elementen ergeben, welche in \(x\)-Richtung steigen bzw. fallen.
Draw(grad(gfu)[0],mesh);
und in \(y\) Richtung
Draw(grad(gfu)[1],mesh);
Mit Hilfe von ngsolve können wir nun die Bilinearfunktion \(A: V \times V \to \mathbb{R}\) und die Linearfunktion \(f: V \to \mathbb{R}\) sehr einfach berechnen.
Es folgt für
wobei hier \(u,v\) stellvertretend für \(\varphi_i, \varphi_j\in V\) steht. Für die Definition der Bilinearfunktion stehen in ngsolve sogenannte Proxy-Funktionen zur Verfügung. Wobei zwischen \(u\) und \(v\) unterschieden werden muss. Für \(u\) benutzen wir TrialFunctions und \(v\) TestFunctions.
u = V.TrialFunction()
v = V.TestFunction()
Damit können wir die Bilinearfunktion definieren, wobei in ngsolve das Volumenintegral \(dV\) mit dx bezeichnet wird. Für Oberflächenintegrale steht ds zur Verfügung.
A = BilinearForm(V)
A += grad(u) * grad(v)*dx
und analog für die Linearform
f = CoefficientFunction(1)
b = LinearForm(V)
b += f*v*dx
Die gegebene Funktion \(f(x)\) der rechten Seite können wir mit sogenannten CoefficientFunction definieren.
Damit haben wir die Bilinearform, welche im endlichdimensionalen mit Hilfe einer Matrix und die Linearform, welche mit einem Vektor beschrieben werden kann definiert, aber noch nicht berechnet. Die Berechnung derer nennt man auch Assembling.
A.Assemble()
b.Assemble();
Die Matrix \(A\) ist „sparse“ gespeichert. Das bedeutet, dass nur die Matrix Einträge gespeichert werden, für welche wir potentiell einen Eintrag erhalten. Für den ganzen Rest der Matrix wird der Speicher gar nicht allokiert. Grundsätzlich haben wir hier alle Freiheitsgrade:
print(A.mat)
Row 0: 0: 1 4: -0.5 15: -0.5
Row 1: 1: 0.895075 6: -0.377531 7: -0.378808 18: -0.138736
Row 2: 2: 1 9: -0.5 10: -0.5
Row 3: 3: 1 12: -0.5 13: -0.5
Row 4: 0: -0.5 4: 1.92156 5: -0.31533 15: -0.15374 16: -0.95249
Row 5: 4: -0.31533 5: 1.8612 6: -0.198542 16: -0.307165 17: -1.04016
Row 6: 1: -0.377531 5: -0.198542 6: 1.79993 17: -0.395887 18: -0.827968
Row 7: 1: -0.378808 7: 1.84286 8: -0.324152 18: -0.918526 19: -0.22137
Row 8: 7: -0.324152 8: 1.79252 9: -0.271716 19: -0.860521 20: -0.336129
Row 9: 2: -0.5 8: -0.271716 9: 2.02128 10: -0.0759864 20: -1.17357
Row 10: 2: -0.5 9: -0.0759864 10: 1.81976 11: -0.220817 20: -0.288822 21: -0.734131
Row 11: 10: -0.220817 11: 1.84084 12: -0.448101 21: -0.875576 22: -0.296345
Row 12: 3: -0.5 11: -0.448101 12: 1.87 13: -0.26789 22: -0.654007
Row 13: 3: -0.5 12: -0.26789 13: 1.84321 14: -0.506823 22: -0.367252 23: -0.201248
Row 14: 13: -0.506823 14: 2.01367 15: -0.420679 23: -1.08617
Row 15: 0: -0.5 4: -0.15374 14: -0.420679 15: 1.79625 16: -0.418051 23: -0.303778
Row 16: 4: -0.95249 5: -0.307165 15: -0.418051 16: 3.61084 17: -0.609253 23: -0.717205 24: -0.606678
Row 17: 5: -1.04016 6: -0.395887 16: -0.609253 17: 3.78711 18: -0.965502 24: -0.77631
Row 18: 1: -0.138736 6: -0.827968 7: -0.918526 17: -0.965502 18: 3.86126 19: -0.936881 24: -0.073651
Row 19: 7: -0.22137 8: -0.860521 18: -0.936881 19: 3.63019 20: -0.534253 24: -0.503238 25: -0.573927
Row 20: 8: -0.336129 9: -1.17357 10: -0.288822 19: -0.534253 20: 3.74798 21: -0.678509 25: -0.73669
Row 21: 10: -0.734131 11: -0.875576 20: -0.678509 21: 3.72565 22: -0.616041 25: -0.821391
Row 22: 11: -0.296345 12: -0.654007 13: -0.367252 21: -0.616041 22: 3.58077 23: -0.913832 24: -0.139859 25: -0.593436
Row 23: 13: -0.201248 14: -1.08617 15: -0.303778 16: -0.717205 22: -0.913832 23: 3.76762 24: -0.545392
Row 24: 16: -0.606678 17: -0.77631 18: -0.073651 19: -0.503238 22: -0.139859 23: -0.545392 24: 3.67338 25: -1.02825
Row 25: 19: -0.573927 20: -0.73669 21: -0.821391 22: -0.593436 24: -1.02825 25: 3.7537
Wir können diese Matrix (zumindest solange sie klein ist!) auch als vollbesetzte „dense“ Matrix betrachten:
rows,cols,vals = A.mat.COO()
denseA = np.zeros((np.max(rows)+1,np.max(rows)+1))
k=0
for i,j in zip(rows,cols):
denseA[i,j] = vals[k]
k+=1
plt.spy(denseA)
plt.show()
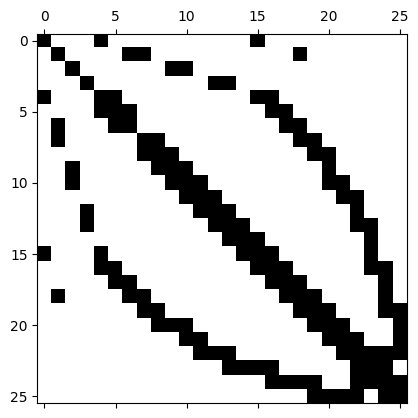
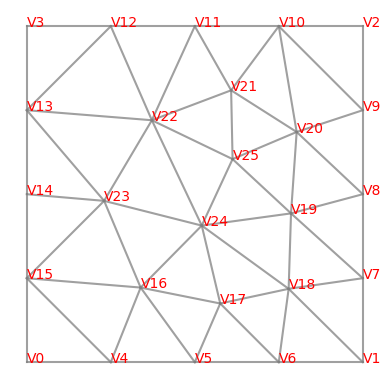
Das Pattern der Matrixeinträge hängt von der Nummerierung der Knoten (aus dem Meshing) und damit der Freiheitsgrade für den FEM Ansatz erster Ordnung ab.
for e in mesh.edges:
line = np.array([mesh.vertices[v.nr].point for v in e.vertices])
plt.plot(line[:,0],line[:,1],c='gray',alpha=0.75)
for v in mesh.vertices:
plt.text(*v.point,v,color='red')
plt.gca().set_axis_off()
plt.gca().set_aspect(1)
plt.show()
ind = np.arange(freedofsnp.shape[0])[freedofsnp]
plt.spy(denseA[np.ix_(ind,ind)])
plt.show()
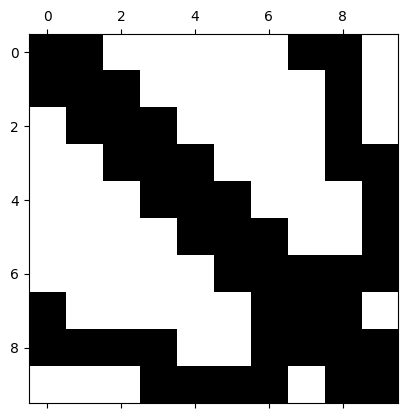
Lösen wir das System für die inneren Freiheitsgrade:
gfu.vec.data = A.mat.Inverse(freedofs=V.FreeDofs())*b.vec
Draw(gfu,mesh,'u');
