9.2.1. Eindimensionaler Fall#
Im eindimensionalen Fall ist eine Zerlegung des Rechengebietes gegeben durch die Teilintervalle \(T_i = [x_i,x_{i+1}]\), wobei die Punkte
gegeben sind. Es gilt daher
Wir betrachten nun die Matrix \(A\) (9.4). Die praktische Berechnung führt nicht über alle Kombinationen \(j, k = 1, \ldots, n\). Die Basis Funktionen sind abhängig von der Zerlegung und können daher nicht vorab definiert werden. Ziel des Assembling ist, die Integration einmal mit Hilfe eines Referenz-Intervalls / Referenz-Elements durchzuführen und auf diese Berechnung zurück zu greifen.
Dazu betrachtet man das Integral in jedem Teilintervall und summiert diese auf
Mit der Transformation
folgt für das Integral
Sei nun \(\tilde{\varphi}(t)\) die auf dem Einheitsintervall \([0,1]\) definierte Basisfunktion, dann gilt
Für die Ableitung folgt somit
Schreibt man das Integral (9.6) mit den Basisfunktionen auf dem Einheitsintervall, so folgt
Da die Transformation eine affine Funktion ist (\(\sigma, \sigma^{-1}\) sind Polynome ersten Grades), gilt \(\dot{\sigma}_i=x_{i+1}-x_i\). Für die globale Steifigkeitsmatrix \(A\) folgt somit
wobei das Integral stets über das Einheitsintervall geht. Wir können daher den finite Element Ansatz auf dem Einheitsintervall studieren und die globale Matrix durch Addition an den entsprechenden Matrixeinträgen zusammenstellen (man spricht hier vom Assembling).
Das Produkt \(\tilde{\varphi}_j(t)\cdot \tilde{\varphi}_k(t)\) ist für fast alle \(j, k\) Kombinationen null. In der Abbildung Abb. 9.4 ist der Fall für Polynome mit Grad 1 dargestellt. In der Abbildung Abb. 9.5 sind die Kombinationen der lokalen Basisfunktionen für unterschiedliche Polynomgrade dargestellt.
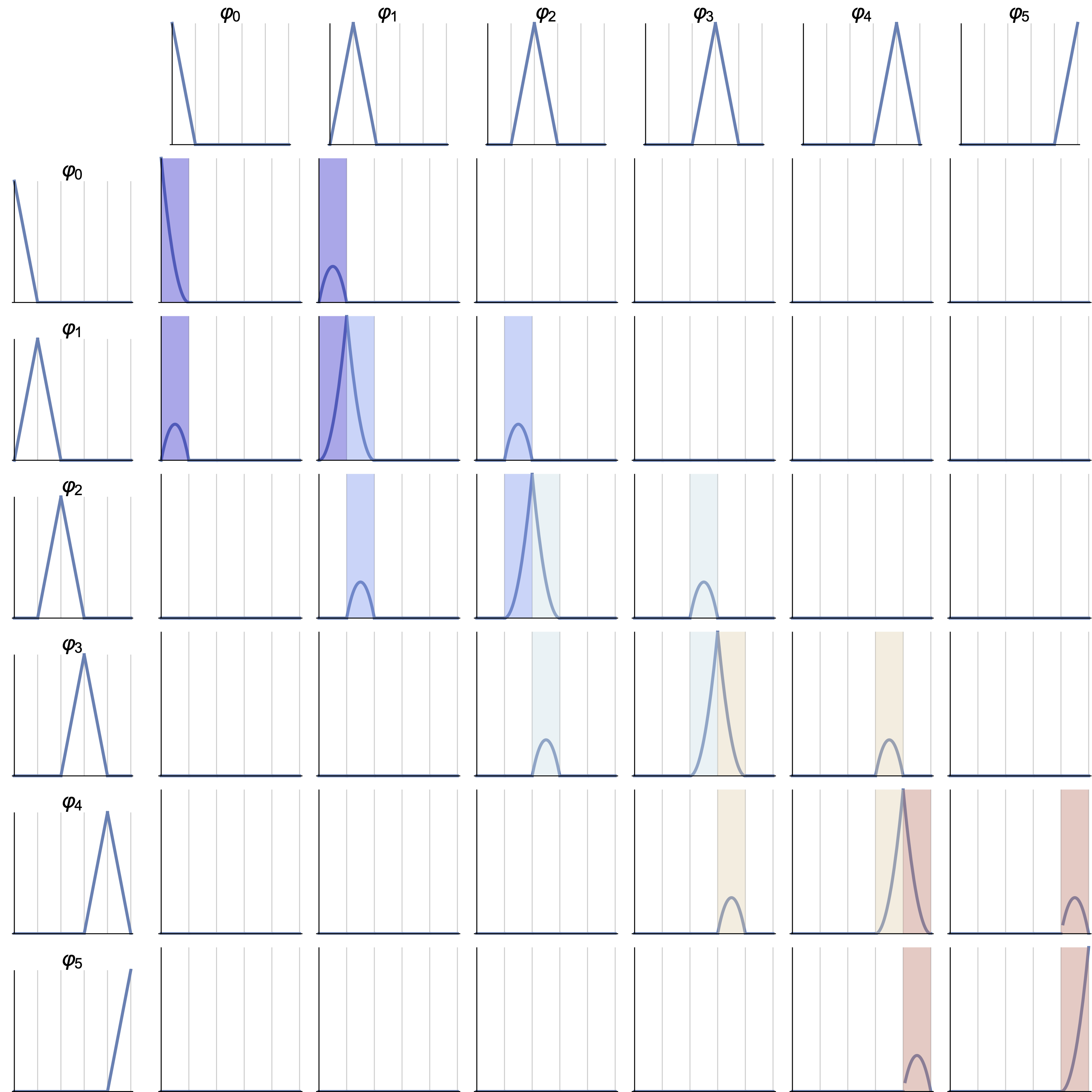
Abb. 9.4 Produkt \(\varphi_j \cdot \varphi_k\) auf dem Intervall \([0,1]\) für stückweise Polynome mit Grad 1.#

Abb. 9.5 Lokale Kombinationen \(\varphi_j \cdot \varphi_k\) der nodalen FEM Basisfunktionen auf dem Einheitsintervall \([0,1]\).#
Praktisch können wir die globale Matrix mit Hilfe der lokalen Elementmatrix (farbige identische Matrizen in der Abbildung Abb. 9.4) berechnen.
Definition 9.1 (Elementmatrizen)
Man nennt die Matrix
Elementsteifigkeitsmatrix
und
Elementmassenmatrix, wobei \(p\) der maximale Polynomgrad der Basisfunktionen sei.
Die Berechnung der globalen Matrix \(A\) erfolgt nun mit Hilfe der im Voraus berechneten lokalen Elementmatrizen \(A_e\). Dabei muss spezifiziert werden, wo in der globalen Matrix \(A\) die Einträge der lokalen Matrix \(A_e\) abhängig vom Element \(T_i\) gespeichert werden müssen. Sei \(T\) die Abbildung der lokalen zu den globalen Freiheitsgrade
wobei \(n\) die Anzahl Elemente, \(p\) den Polynom Grad der lokalen Basisfunktionen und \(N\) die globale Anzahl Freiheitsgrade bezeichne. Für den eindimensionalen Fall mit Polynome ersten Grades die Abbildung \(T\) gegeben durch
Die globalen Matrizen können daher mit lokalen Elementmatrizen wie folgt berechnet werden
Algorithm 9.1 (Assembling Bilinearform)
for \(i\) in range(\(n\)):
compute local Matrix \(A_e\)
for \(j\) in range(\(p\)):
for \(k\) in range(\(p\)):
\(A_{T(i,j),T(i,k)}\) += \(\frac{1}{h_i}\cdot {A_e}_{j,k}\)
Remark 9.1
Im Fall, dass die zu lösende Differentialgleichung konstante Koeffizienten hat, kann die Elementmatrix vorab berechnet werden.
Sind ortsabhängige Koeffizienten vorhanden, muss die Elementmatrix für jedes Element lokal berechnet werden. Die Definition der Basisfunktionen (shape functions) erfolgt auch in dem Fall nur auf dem Referenzelement.
Die Dimension der Elementmatrix ist vom Polynomgrad \(p\) abhängig. In den Tabellen Abschnitt 9.2.3 sind die \(S_e, M_e\) für die Polynomgrade \(p=1,2,3\) berechnet, analog zur Abbildung Abb. 9.5.
Das Assembling der Systemmatrix (Matrix der Bilinearform) des Einstiegsbeispiels (9.2) mit Hilfe Elemente erster Ordnung kann wie folgt umgesetzt werden:
Show code cell content
import numpy as np
from pandas import DataFrame
def highlight_ortho(s):
is_ortho = np.abs(s) < 1e-13
return ['background-color: yellow' if v else '' for v in is_ortho]
import matplotlib.pyplot as plt
from myst_nb import glue
def uanalytic(x):
return -0.5*x*(x-1)
# Elementsteifigkeitsmatrix
order = 1
Ae = np.array([[1,-1],[-1,1]])
# Zerlegung des Gebiets
n=5;a=0;b=1
xi = np.linspace(a,b,n+1)
h = xi[1:]-xi[:-1]
# lokal - global mapping
N = n+1
T = np.array([[i,i+1] for i in range(N)])
# Globale Steiffigkeitsmatrix
A = np.zeros((N,N))
# Loop über Elemente (Assembling)
for i in range(n):
for j in range(order+1):
for k in range(order+1):
A[T[i,j],T[i,k]] += Ae[j,k]/h[i]
A
array([[ 5., -5., 0., 0., 0., 0.],
[-5., 10., -5., 0., 0., 0.],
[ 0., -5., 10., -5., 0., 0.],
[ 0., 0., -5., 10., -5., 0.],
[ 0., 0., 0., -5., 10., -5.],
[ 0., 0., 0., 0., -5., 5.]])
Für die Linearform folgt analog
Mit Hilfe des lokal-global Mapping (9.8) und den Referenz Basisfunktionen folgt
Algorithm 9.2 (Assembling Linearform)
for \(i\) in range(\(n\)):
compute local Vector \(f_e\)
for \(j\) in range(\(p\)):
\(f_{T(i,j)}\) += \(h_i\cdot {f_e}_{j}\)
Für das Beispiel folgt:
from scipy.integrate import fixed_quad
# Referenz Elementfunktionen
def phi(t,i):
if i == 0:
return 1-t
else:
return t
# Rechteseite der DGL
def func(x):
return np.ones_like(x)
# Koordinaten Transformation
def sigma(t,i):
return xi[i]+t*h[i]
# Globale Vektor der Linearform
f = np.zeros(N)
# Loop über Elemente (Assembling)
for i in range(n):
# berechne lokaler Vektor
fe = [np.sum([fixed_quad(lambda t: func(sigma(t,i))*phi(t,j),
xi[k],xi[k+1],n=2*order)[0]
for k in range(n)]) for j in range(order+1)]
for j in range(order+1):
f[T[i,j]] += h[i]*fe[j]
f
array([0.1, 0.2, 0.2, 0.2, 0.2, 0.1])
Mit der Berücksichtigung der Dirichlet Randbedingung folgt die numerische Lösung, abgebildet in der Abbildung Abb. 9.6.
Show code cell content
ui = np.zeros_like(xi)
ui[1:-1] = np.linalg.solve(A[1:-1,1:-1],f[1:-1])
xp = np.linspace(0,1,400)
fig, ax = plt.subplots(figsize=(6, 2))
ax.plot(xi,ui,label='FEM Lösung')
ax.plot(xp,uanalytic(xp),label='exakte Lösung')
ax.legend()
glue("FEM_1d_p1_solutionexmp_fig2", fig, display=False)
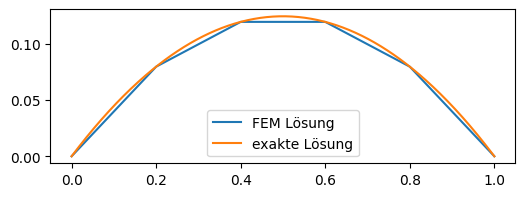
Abb. 9.6 FEM 1d affine Basisfunktionen#
