11.2. Direkte Gleichungslöser

Die FEM Matrix der Dimension hat nach geeignetem Umordnen (Nummerierung der Knoten, Dreiecke, etc.) oft eine Block-Struktur. Im Gegensatz zu direkten Löser basierend auf Faktorisierungsmethoden, wie z.B. die oben erwähnte LR-Zerlegung, können Block-eliminations Methoden noch effizienter sein.

Siehe auch

Beispiele zur Matrixstruktur

Wir teilen die Unbekannten in zwei Gruppen und schreiben die Gleichung \(A\,u = f\) neu als Blocksystem

\[\begin{split}\begin{pmatrix} A_{11} & A_{12}\\ A_{21} & A_{22}\end{pmatrix}\ \begin{pmatrix}u_1\\u_2\end{pmatrix} = \begin{pmatrix}f_1\\f_2\end{pmatrix}.\end{split}\]

Als erstes berechnen wir \(u_1\)

\[u_1 = A_{11}^{-1}\,(f_1-A_{12}u_2)\]

und die Schur-Komplement Gleichung um \(u_2\) zu bestimmen

\[\underbrace{(A_{22} - A_{21}A_{11}^{-1}A_{12})}_{=S}\,u_2 = f_2 - A_{21} A_{11}^{-1} f_1.\]

Definition 11.1 (Schur-Komplement)

Die Matrix

\[S = A_{22} - A_{21}A_{11}^{-1}A_{12}\]

heisst Schur-Komplement \(S_{11}\) in \(A\).

Diese Block-Faktorisierung wird in sub-structuring Algorithmen benutzt. Dabei zerlegt man das Gebiet in \(m\times m\) Untergebiete und teilt die Unbekannten in innere und koppelnde Unbekannte auf. Nun kann die Faktorisierung der Blöcke mit den inneren Unbekannten und die Berechnung des Schur-Komplements parallel berechnet werden. Die Eliminierung der internen Unbekannten kann mit sogenannten hierarchischen sub-structuring Algorithmen (z.B. nested dissection) durchgeführt werden.

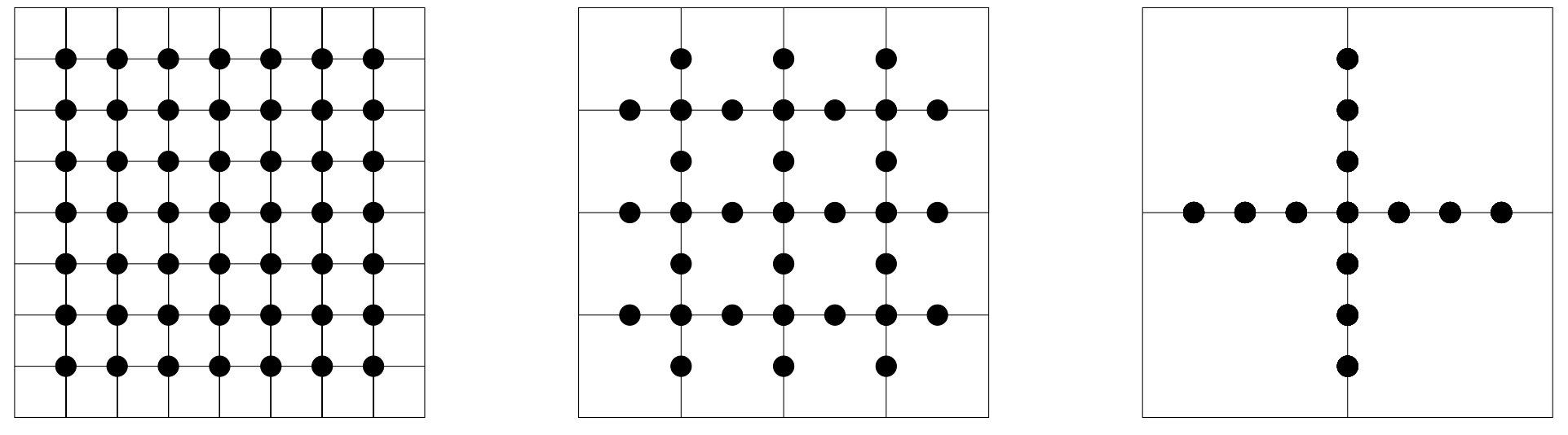
Abb. 11.1 Hierarchische Elimination

Hierarchische Elimination funktioniert bei strukturierten Gitter sehr gut. Man kann sie jedoch auch unstrukturierten Gitter anwenden. In dem Fall basiert die Ordnung auf dem minimalen Grad der Kopplung. Nacheinander werden die Unbekannten mit den wenigsten Verbindungen im Matrixgraphen eliminiert.

In 2D ist eine direkte Methode mit optimaler Anordnung sehr effizient. In 3D ist die Situation für den direkten Löser schlechter.

Bemerkung

In der Praxis bedeutet das in aller Regel, dass 2D Probleme einfach mit direkten Löser berechnet werden können. Hingegen bei 3D Problemen benötigen wir zwingend einen anderen Ansatz.

Help on method Inverse in module ngsolve.la:

Inverse(...) method of ngsolve.la.SparseMatrixd instance
    Inverse(self: ngsolve.la.BaseMatrix, freedofs: pyngcore.BitArray = None, inverse: str = '') -> BaseMatrix
    
    Calculate inverse of sparse matrix
    Parameters:
    
    freedofs : BitArray
    If set, invert only the rows/columns the matrix defined by the bit array, otherwise invert the whole matrix
    
    inverse : string
    Solver to use, allowed values are:
        sparsecholesky - internal solver of NGSolve for symmetric matrices
        umfpack        - solver by Suitesparse/UMFPACK (if NGSolve was configured with USE_UMFPACK=ON)
        pardiso        - PARDISO, either provided by libpardiso (USE_PARDISO=ON) or Intel MKL (USE_MKL=ON).
                         If neither Pardiso nor Intel MKL was linked at compile-time, NGSolve will
                         look for libmkl_rt in LD_LIBRARY_PATH (Unix) or PATH (Windows) at run-time.