11.3.2. Jacobi und Gauss-Seidel - Verfahren#
Jacobi-Verfahren#
Analog zum Richardson Verfahren basiert das Verfahren auf der Fixpunkt Iteration. Ausgehend vom linearen Gleichungssystem
wird die Matrix \(A\) additiv zerlegt:
wobei \(D\) die Diagonale, \(L\) die untere Dreiecksmatrix ohne Diagonale und \(R\) die obere Dreiecksmatrix ohne Diagonale von \(A\) sei. Das Jacobi-Verfahren ist als Fixpunkt-Iteration gegeben durch
Da \(D\) diagonal ist, ist \(D^{-1}\) einfach zu berechnen es folgt
wobei die Multiplikation mit der Diagonalmatrix nicht als Matrix-Multiplikatin umgesetzt wird. Eine elementweise Vektormultiplikation ist schneller.
Das Verfahren konvergiert, falls \(2 D-A\) positiv definit ist.
Gauss-Seidel Verfahren#
Analog zum Jacobi-Verfahren gilt daher wiederum
Im Fall des Gauss-Seidel-Verfahren ist die Fixpunktiteration gegeben durch
Der Unterschied ist daher, dass hier ausgenutzt wird, dass \(L\) eine untere Dreiecksmatrix ohne Diagonale ist und daher \(x^{k+1}\) sukzessive berechnet werden kann.
Anwendung Jacobi Verfahren#
Wir wenden das Verfahren auf das Modellproblem
an.
from ngsolve import *
from netgen.geom2d import unit_square
from ngsolve.webgui import Draw
import matplotlib.pyplot as plt
from myst_nb import glue
Diskretierung der schwachen Gleichung mit FEM 1. Ordnung:
mesh = Mesh(unit_square.GenerateMesh(maxh=0.1))
V = H1(mesh, order=1, dirichlet='bottom|right|top|left')
u = V.TrialFunction()
v = V.TestFunction()
a = BilinearForm(grad(u)*grad(v)*dx+10*u*v*dx).Assemble()
f = LinearForm(1*v*dx).Assemble()
gfu = GridFunction(V)
Wir nutzen das CSR Modul von scipy um das reduzierte Problem für die freien Freiheitsgrade zu lösen.
import scipy.sparse as sp
import numpy as np
from numpy.linalg import norm
rows,cols,vals = a.mat.COO()
ind = np.arange(V.ndof)[np.array(V.FreeDofs())]
# Reduktion auf die freien Freiheitsgrade der Systemmatrix
A = sp.csr_matrix((vals,(rows,cols)))
A = A[np.ix_(ind,ind)]
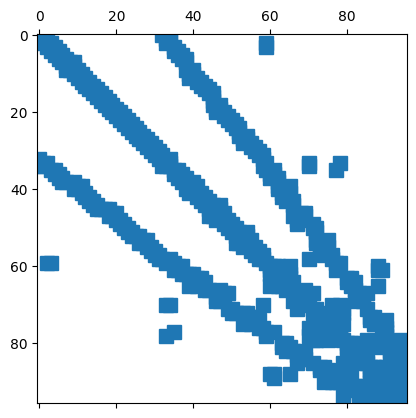
plt.spy(A)
plt.show()
# Reduktion auf die freien Freiheitsgrade der rechten Seite
fd = np.array(f.vec)[ind]
alpha = 1
d = A.diagonal()
L = -sp.tril(A,-1)
R = -sp.triu(A,1)
LR = L+R
sol = np.zeros(V.ndof)
err0 = Norm(f.vec)
its = 0
errs = []
reltol = 1e-8
maxiter = 10000
while True:
sol[ind] = LR @ sol[ind]+fd
sol[ind] /= d
err = norm(A@sol[ind]-fd)
errs.append(err)
#print ("iteration", its, "res=", err)
if err < reltol * err0 or its > maxiter: break
its = its+1
print ("needed", its, "iterations")
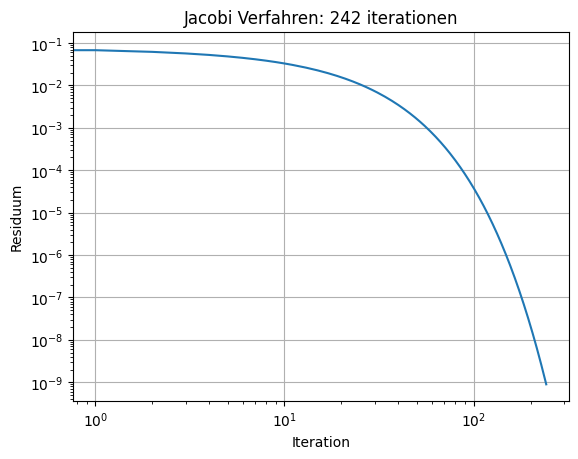
needed 242 iterations
fig, ax = plt.subplots()
ax.loglog(errs)
ax.grid()
ax.set_title('Jacobi Verfahren: '+str(its)+' iterationen')
ax.set_xlabel('Iteration')
ax.set_ylabel('Residuum')
#plt.savefig('FEM_JacobiVerfahren_fig.png')
glue("FEM_JacobiVerfahren_fig", fig, display=False)
gfu.vec[:] = sol
Draw(gfu,mesh,'u');
Anwendung Gauss-Seidel Verfahren#
In jedem Iterationsschritt wird das Gleichungssystem mit Hilfe von Rückwärtseinsetzen gelöst
from scipy.sparse.linalg import spsolve_triangular
C = sp.tril(A,format='csr')
sol = np.zeros(V.ndof)
err0 = Norm(f.vec)
its = 0
errs = []
while True:
r = R@sol[ind]+fd
sol[ind] = spsolve_triangular(C,r)
err = norm(A@sol[ind]-fd)
errs.append(err)
#print ("iteration", its, "res=", err)
if err < 1e-8 * err0 or its > 10000: break
its = its+1
print ("needed", its, "iterations")
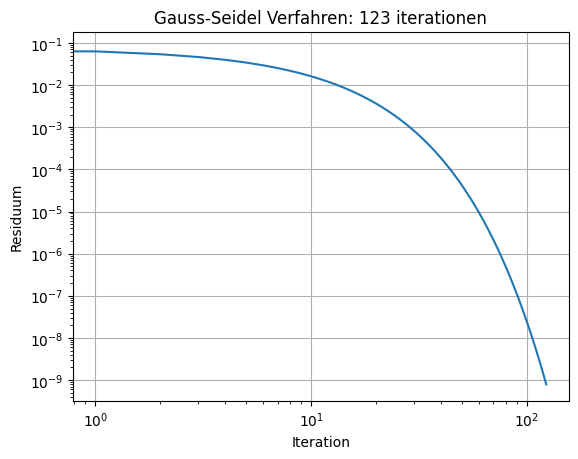
needed 123 iterations
fig2, ax = plt.subplots()
ax.loglog(errs)
ax.grid()
ax.set_title('Gauss-Seidel Verfahren: '+str(its)+' iterationen')
ax.set_xlabel('Iteration')
ax.set_ylabel('Residuum')
#plt.savefig('FEM_Gauss-SeidelVerfahren_fig.png')
glue("FEM_Gauss-SeidelVerfahren_fig", fig2, display=False)
gfu.vec[:] = sol
Draw(gfu,mesh,'u');
