11.3.1. Richardson Verfahren#
Die Theorie folgt direkt dem iFEM Jupyter-Notebook, wobei wir für das Beispiel Dirichlet Randbedingungen implementieren.
Fixpunkt Iteration#
Sei \(C\) eine reguläre Matrix und \(\alpha\in\mathbb{R}^+\) ein Dämpfungsfaktor. Dann ist das lineare Gleichungssystem äquivalent zur Fixpunktgleichung
Daraus ergibt sich die Fixpunkt Iteration, auch einfache Iteration oder Richardson Iteration genannt:
wobei der Startwert \(x_0\) gegeben ist.
Sei \(x^*\) eine Lösung von (11.1) und
der Iterationsfehler. Dann gilt für den neuen Fehler
Der neue Fehler ergibt sich durch die Iterationsmatrix oder Fehlerübergangsmatrix
als
Sei \(\|\cdot\|\) eine beliebige Vektornorm und
die zugehörige Matrixnorm (Operatornorm vgl. (4.2)). Damit gilt für den neuen Fehler (vgl. (4.3))
Hinreichend für die Konvergenz ist damit die Existenz einer Matrixnorm mit
Vorkonditionierer#
Die Matrix \(C\) wird Vorkonditionierer (Preconditioner) genannt. Sie soll zwei Eigenschaften erfüllen:
Die Matrix-Vektormultiplikation mit \(C^{-1}\cdot r\) soll billig sein.
Die Matrix \(C\) soll eine gute Approximation zu \(A\) sein.
Zur Wahl der Matrix \(C\)
Wählt man zum Beispiel \(C = \mathbb{1}\) oder etwas besser \(C = \mathop{diag} A\), dann ist die Operation \(C^{-1}\cdot r\) sehr billig. Die Approximation \(C \approx A\) kann aber schlecht sein.
Wählt man hingegen \(C = A\) und \(\alpha = 1\), dann ist die zweite Eigenschaft best-möglich erfüllt:
\[M = \mathbb{1} - \alpha C^{-1} A = \mathbb{1} - A^{-1}A = 0.\]Es gilt daher \(\|M\| = 0\).
Die Invertierung von \(C\) ist jetzt aber genau das ursprüngliche Problem.
Ziel ist es Vorkonditionierer mit beiden Eigenschaften zu finden.
Richardson Iteration#
Im Richardson Verfahren wird die Matrix \(C=\mathbb{1}\) gesetzt. Damit folgt für die Fehlerübergangsmatrix
Für die Überprüfung der Konvergenz gibt es zwei Möglichkeiten:
den Konvergenzradius zu überprüfen
\[\rho(\mathbb{1} - \alpha A) = \max_{\lambda\in\sigma(\mathbb{1} - \alpha A)} |\lambda| < 1\]eine geeignete Norm \(\|\cdot\|\) finden, so dass die Matrixnorm
\[|\!|\!|\mathbb{1} - \alpha A|\!|\!|:=\sup_{x\in\mathbb{R}^n}\frac{\|(\mathbb{1} - \alpha A) x\|}{\|x\|} < 1\]erfüllt ist.
Optimieren des Dämpfungsfaktors#
Sei \(A\) symmetrisch und positiv definit. Damit sind die Eigenwerte \(\sigma(A) = \{\lambda_i\in\mathbb{R}\}\) mit \(0<\lambda_1 \le \lambda_2 \ldots \le \lambda_n\).
Die Eigenwerte der Fehlerübergangsmatrix \(M = \mathbb{1} - \alpha\,A\) sind in dem Fall gegeben durch \(\{1-\alpha\, \lambda_i\}\). Wenn wir daher
wählen, folgt \(\rho(M) < 1\) und damit eine konvergente Itertation.
Der Spektralradius von \(M\) ist gegeben durch
Das Maximum ist minimiert, wenn wir \(\alpha\) optimal wählen, daher
Somit sei
was zur optimalen Konvergenzrate
führt, wobei mit \(\kappa(A)\) die Konditionszahl \(\kappa(A) = \lambda_{\max}(A) / \lambda_{\min}(A)\) bezeichnet sei.
Nach \(N\) Iterationen ist der Fehler um den Faktor
reduziert. Um die Fehlerreduktion \(\epsilon\) zu erreichen, sind
Iterationen notwendig.
Anwendung auf Modellproblem#
Wir wenden das Verfahren auf das Modellproblem
an.
from netgen.geom2d import unit_square
from ngsolve import *
from ngsolve.webgui import Draw
import matplotlib.pyplot as plt
from myst_nb import glue
Diskretierung der schwachen Gleichung mit FEM 1. Ordnung:
mesh = Mesh(unit_square.GenerateMesh(maxh=0.1))
V = H1(mesh, order=1, dirichlet='bottom|right|top|left')
u = V.TrialFunction()
v = V.TestFunction()
a = BilinearForm(grad(u)*grad(v)*dx+10*u*v*dx).Assemble()
f = LinearForm(1*v*dx).Assemble()
gfu = GridFunction(V)
Wir nutzen das CSR Modul von scipy um das reduzierte Problem für die freien Freiheitsgrade zu lösen.
import scipy.sparse as sp
import numpy as np
from numpy.linalg import norm
Für die reduzierte Systemmatrix folgt
rows,cols,vals = a.mat.COO()
ind = np.arange(V.ndof)[np.array(V.FreeDofs())]
# Reduktion auf die freien Freiheitsgrade der Systemmatrix
A = sp.csr_matrix((vals,(rows,cols)))
A = A[np.ix_(ind,ind)]
plt.spy(A)
plt.show()
# Reduktion auf die freien Freiheitsgrade der rechten Seite
fd = np.array(f.vec)[ind]
Eine Approximation der Dämpfung wird mit Hilfe von ein paar Potenziterationen bestimmt:
hv = np.random.rand(ind.shape[0])
hv /= norm(hv)
for k in range(20):
hv2 = A@hv
rho = norm(hv2)
print(rho)
hv = 1/rho*hv2
1.93892201500378
4.035376374773378
4.391698016287348
4.537850601281457
4.632750753289792
4.708700926551877
4.775311720432426
4.835756943570336
4.891018048080095
4.941275873037939
4.9864812644106795
5.02661571053674
5.061795316336084
5.092286001475633
5.118472911718596
5.140813353082259
5.159791060375444
5.175880311802537
5.189522081405155
5.201110965264451
Richardson Verfahren anwenden
alpha = 1 / rho
sol = np.zeros(V.ndof)
err0 = norm(fd)
its = 0
errs = []
reltol = 1e-8
maxiter = 10000
while True:
r = fd - A * sol[ind]
err = norm(r)
errs.append(err)
#print ("iteration", its, "res=", err)
sol[ind] += alpha * r
if err < reltol * err0 or its > maxiter: break
its = its+1
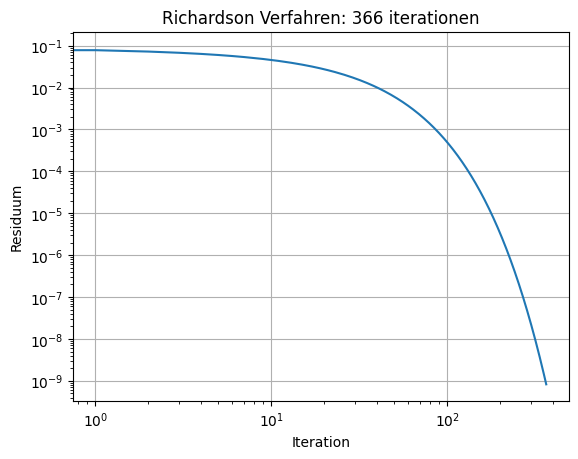
print ("needed", its, "iterations")
needed 361 iterations
Für die Abschätzung der Anzahl notwendiger Iterationen erhalten wir:
import scipy.sparse.linalg as spl
np.linalg.cond(A.todense())*np.abs(np.log(1e-8))
np.float64(382.75172899276646)
Achtung, diese Berechnung funktioniert nur für wenig Freiheitsgrade.
fig, ax = plt.subplots()
ax.loglog(errs)
ax.grid()
ax.set_title('Richardson Verfahren: '+str(its)+' iterationen')
ax.set_xlabel('Iteration')
ax.set_ylabel('Residuum')
#plt.savefig("FEM_RichardsonVerfahren_fig.png")
glue("FEM_RichardsonVerfahren_fig", fig, display=False)
Schreiben wir die Lösung wieder zurück in die GridFunction von ngsolve können wir die Lösung visualisieren:
gfu.vec[:] = sol
Draw(gfu,mesh,'u');