5.2. Sobolevräume

Mit den Sobolevräumen kommt nun die Ableitung von Elemente aus dem \(L_2(\Omega)\) ins Spiel. Wir definieren den Sobolevraum \(H^k(\Omega)\) wie folgt

Definition 5.3 (Sobolevraum \(H^k(\Omega)\))

Unter dem Sovolevraum \(H^k(\Omega)\) versteht man den linearen Raum aller linearen Funktionale \(F\) auf \(C_0^\infty(\Omega)\), für die \(F\) und sämtliche Ableitungen \(D^pF\) der Ordnung \(|p|\le m\) zu \(L_2(\Omega)\) gehören:

\[H^k(\Omega) := \{F\in L_2(\Omega) | D^p F \in L_2(\Omega), |p|\le k\}.\]

Mit \(x = (x_1, \ldots, x_n)^T \in \mathbb{R}^n\), dem Multiindex \(p = (p_1, \ldots, p_n)\), \(p_i\in \mathbb{N}_0\) für \(i=1,\ldots, n\) und

\[D^p = \left(\frac{\partial}{\partial x_1}\right)^{p_1} \ldots \left(\frac{\partial}{\partial x_n}\right)^{p_n},\]

sowie \(|p| = p_1 + \ldots + p_n\).

Nicht klar ist an dieser Stelle, was \(D^p F\) zu bedeuten hat, da \(F\) ein beschränktes lineares Funktional ist. Der klassische Ableitungsbegriff genügt nicht der in der Definition benutzten Ableitung, da dieser für Funktionale verallgemeinert werden muss.

Betrachten wir das Ganze mit Hilfe eines eindimensionalen Gebietes \(\Omega = [0,1]\) und für Funktionale \(F_u \in L_2([0,1])\), welche durch Funktionen \(u\in C^1([0,1])\) induziert sind:

\[F_u \varphi = \int_0^1 u(t) \varphi(t) dt\quad \text{für}\ \varphi\in C_0^\infty([0,1]).\]

Die Ableitung \(\frac{\partial}{\partial x} F_u\) definieren wir wie folgt:

\[\frac{\partial}{\partial x} F_u := F_{\frac{\partial u}{\partial x}}\]

Mit der Definition und partieller Integration erhalten wir

\[\begin{split}\begin{split}\frac{\partial}{\partial x} F_u = F_{\frac{\partial u}{\partial x}} & = \int_0^1 \frac{\partial u}{\partial x}(x) \varphi(x) dx \\ & = \underbrace{\frac{\partial}{\partial x} (u(x) \varphi(x)) \Big|_0^1}_{=0, \text{da}\ \varphi(0)=\varphi(1) = 0!} - \int_0^1 u(x) \frac{\partial \varphi}{\partial x}(x) dx\\ & = - \int_0^1 u(x) \frac{\partial \varphi}{\partial x}(x) dx.\end{split}\end{split}\]

Wir erhalten somit

\[\frac{\partial}{\partial x} F_u = - F_u (\frac{\partial \varphi}{\partial x})\quad\text{für}\quad \varphi \in C_0^\infty([0,1]).\]

Oder für mehrdimensionale Gebiete \(\Omega\)

\[\frac{\partial}{\partial x} F_u = - F_u (\frac{\partial \varphi}{\partial x})\quad\text{für}\quad \varphi \in C_0^\infty(\Omega).\]

Damit können wir eine verallgemeinerte Ableitung definieren, welche auch auf Funktionen \(u(x)\), welche selber nicht im klassischen Sinne differenzierbar sind, anwendbar ist:

Definition 5.4 (Verallgemeinerte Ableitung (generalized derivative))

Für \(u\in L_2(\Omega)\) definieren wir \(g \in L_2(\Omega)\) als die verallgemeinerte Ableitung \(D^pu\) von \(u\) wobei

(5.1)\[\int_\Omega g(x) \varphi(x) dx = (-1)^{|p|} \int_\Omega u(x) D^p\varphi dx\quad \forall\ \varphi\in C_0^\infty(\Omega).\]

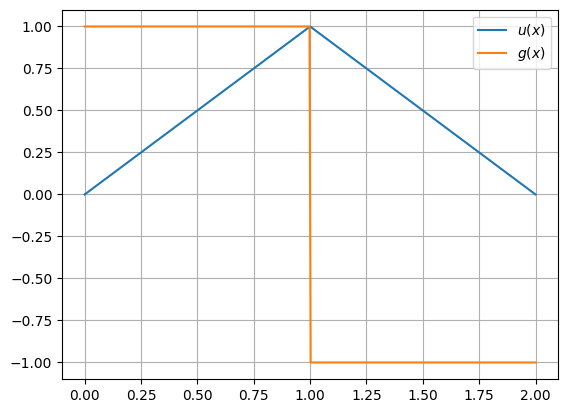
Beispiel: Ein Beispiel einer Funktion die schwach, aber nicht klassisch differenzierbar ist, ist \(u:[0,2] \to \mathbb{R}\) mit

\[\begin{split}u(x) = \begin{cases} x\quad \text{für}\ 0 \le x \le 1\\ 2-x\quad \text{für}\ 1 < x \le 2.\end{cases}\end{split}\]

Die schwache Ableitung \(g(x) := D^1u(x)\) ist die stückweise definierte Ableitung

\[\begin{split}g(x) = \begin{cases} 1\quad \text{für}\ 0 \le x \le 1\\ -1\quad \text{für}\ 1 < x \le 2\end{cases}\end{split}\]

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

xp = np.linspace(0,2,400)
yp = np.zeros_like(xp)
yp[xp<1] = xp[xp<1]
yp[1<=xp] = 2-xp[1<=xp] 
dyp = np.zeros_like(xp)
dyp[xp<1] = 1
dyp[1<=xp] = -1 

plt.plot(xp,yp,label=r'$u(x)$')
plt.plot(xp,dyp,label=r'$g(x)$')
plt.legend()
plt.grid()
plt.show()

Für alle \(v\in C_0^\infty[0,1]\) gilt

\[\begin{split}\begin{split} -\int_0^2 u(x)v'(x) dx & = - \int_0^1 x v'(x) dx - \int_1^2 (2-x) v'(x) dx \\ & = \int_0^1 \left(\frac{d}{dx}x\right) v(x) dx - \big[x v(x)\big]_0^1 + \int_1^2 \left(\frac{d}{dx}2-x\right) v(x) dx - \big[(2-x) v(x)\big]_1^2\\ & = \int_0^1 1 v(x) dx - 1 v(1) + 0 + \int_1^2 (-1) v(x) dx - 0 + 1 v(1)\\ & = \int_0^2 g(x) v(x) dx. \end{split}\end{split}\]

Eine äquivalente oft benutzte Definition der Sobolevräume (leicht allgemeinere) baut auf den lokal integrierbaren Funktionen auf \(\Omega\) auf, gegeben durch

\[L_1^{\text{loc}}(\Omega) = \{u | u_K\in L_1(K)\ \forall\ \text{kompakten Teilmengen}\ K\subset\Omega\}.\]

Der Raum \(L_1^{\text{loc}}\) beinhaltet Funktionen, welche sich sehr schlecht in der Nähe des Randes \(\partial\Omega\) verhalten können.

Beispiele:

• \(e^{e^{1/x}}\) ist in \(L_1^{\text{loc}}(0,1)\).

• Ist \(\Omega\) unbeschränkt, dann ist die Funktion 1 in \(L_1^{\text{loc}}(\Omega)\), aber nicht in \(L_1\). Ist zum Beispiel \(\Omega = \mathbb{R}^n\), dann gilt

\[\int_{\mathbb{R}^n} 1 dx = \infty.\]

Definition 5.5 (Sobolev Räume \(W_p^k(\Omega)\))

Sei \(k\in\mathbb{N}_0\) und \(1 \le p < \infty\), dann definieren wir die Sobolev Normen mit

\[\|u\|_{W_p^k(\Omega)} := \left(\sum_{|\alpha|\le k} \int_\Omega |D^\alpha u(x)|^p dx \right)^{1/p}\]

und die Sobolev Räume mit

\[W_p^k(\Omega) = \big\{u\in L_1^{\text{loc}}(\Omega) | \|u\|_{W_p^k(\Omega)} < \infty\big\}.\]

Ohne Beiweis gilt der Satz

Theorem 5.2

Die Sobolev Räume \(W_p^k(\Omega)\) sind Banach Räume. Der Sobolev Raum \(W_2^k(\Omega) = H^k(\Omega)\) ist ein Hilbertraum.

Beispiel: Wir werden primär den Sobolev Raum \(W_2^1(\Omega) = H^1(\Omega)\) benutzen. Hier gilt für die Norm

\[\|u\|_{H^1(\Omega)} := \left(\sum_{|\alpha|\le 1} \int_\Omega |D^\alpha u(x)|^2 dx \right)^{1/2}\]

und das Skalarprodukt

\[(u,v)_{H^1(\Omega)} = \sum_{|\alpha|\le 1} (D^\alpha u,D^\alpha v)_{L_2} = \sum_{|\alpha|\le 1} \int_\Omega D^\alpha u(x) D^\alpha v(x) dx\]

Siehe auch

Beispiel zur \(H_1\) Norm und Skalarprodukt.