11.3.4. CG - Verfahren#
Die Theorie folgt direkt dem iFEM Jupyter-Notebook, wobei wir für das Beispiel Dirichlet Randbedingungen implementieren.
Die Gradientenmethode ist eine Verbesserung der Richardson-Methode, da sie die spektralen Schranken nicht explizit benötigt. Das Chebyshev-Verfahren (nicht behandelt, vgl. iFEM Jupyter-Notebook Chebyshev) ist ebenso eine Verbesserung des Richardson-Verfahrens, welches die Anzahl der Iterationen von \((\log \varepsilon^{-1}) \, \kappa\) auf \((\log \varepsilon^{-1}) \, \sqrt{\kappa}\) reduziert. Die Methode der konjugierten Gradienten kombiniert beide Vorteile.
Alle erwähnten Methoden benötigen eine Matrix-Vektor-Multiplikation mit der Systemmatrix \(A\) und eine Anwendung des Vorkonditionierungs \(C^{-1}\) pro Iteration, sowie einige Vektoraktualisierungen. Die Gradientenmethode und die konjugierte Gradientenmethode benötigen Skalarprodukte.
Die Idee hinter der CG-Methode ist die Minimierung der Ritz-Funktion
im Krylov-Raum
In jeder Iteration vergrößern wir den zu minimierenden Raum und berechnen den neuen Minimierer. Dies kann effizient durch die Berechnung einer orthogonalen Basis für \({\mathcal K}^n\) durchgeführt werden.
Da jede Polynom-Iteration (wie die Chebyshev-Methode) Schritte \(x^n \in {\mathcal K}^n\) erzeugt, erhalten wir Fehlerschätzungen für die CG-Methode unmittelbar aus der Chebyshev-Methode.
Lösen des Minimierungsproblems#
Angenommen \(V^n\subset {\mathbb R}^N\) sei ein \(n\)-dimensionaler Unterraum, welcher von den Basisvektoren \(p_1, \ldots, p_n\) aufgespannt wird. Sei \(P \in {\mathbb R}^{N \times n}\) gegeben durch die Basisvektoren \(p_k\) als Spaltenvektoren. Wir lösen nun das Minimierungsproblem über dem Unterraum \(V^n\)
Da jedes \(x \in V^n\) als \(x = P y\) mit \(y \in {\mathbb R}^n\) geschrieben werden kann, kann das Minimierungsproblem als
umgeschrieben werden. Die Lösung ist gegeben durch
welche durch Lösen eines niederdimensionalen (\(n \times n\)-dimensionalen) linearen Systems berechnet werden kann. Die original Lösung \(x\) ist gegeben durch
Wenn die Vektoren \(p_i\) \(A\)-orthogonal sind (auch \(A\)-konjugiert genannt), d.h.
dann ist die Matrix \(P^T A\, P\) diagonal, und das Minimierungsproblem kann sehr leicht gelöst werden:
Vergrössert man den Raum \(V^n\) auf \(V^{n+1}\), indem man einen weiteren Vektor \(p_{i+1}\) hinzufügt, der orthogonal zu allen bisherigen \(p_1, \ldots , p_n\) ist, dann kann der Minimierer \(x_{n+1}\) auf \(V^{n+1}\) kostengünstig aus dem Minimierer \(x^n\) auf \(V^n\) aktualisiert werden:
Erweitern des Krylov-Raums#
Nehmen wir an, wir haben den Krylov-Raum \({\mathcal K}^n\) und wir haben den Minimierer \(x_n \in {\mathcal K}^n\) berechnet.
Dann ist der (negative) Gradient von \(f(x) = \tfrac{1}{2} x^T A x - b^T x\) gegeben durch
\({\mathbb R}^N\)-orthogonal zu \({\mathcal K}^n\). Es gilt daher
Wenn \(r_n = 0\) ist, ist das Problem gelöst.
Da \(r_n\ \) \({\mathbb R}^N\)-orthogonal zu \({\mathcal K}^n\) ist, gilt für
Letzteres folgt aus
Da \(x_n\) in \({\mathcal K}^n\) liegt und \(w_n\) durch eine weitere Anwendung von \(C^{-1}\) und \(A\) erhalten wird, erhalten wir \(w_n \in {\mathcal K}^{n+1}\). Zusammen mit der \(C\)-Orthogonalität haben wir
Wir konstruieren nun eine \(A\)-orthogonale Basis mit Hilfe der Gram-Schmidt-Orthogonalisierung:
Hier offenbart sich der Kern der CG-Methode. Für die Skalarprodukte im Zähler gilt
Da \(r^n \; \bot \; {\mathcal K}^n\) und \(C^{-1} A p_i \in {\mathcal K}^{i+1}\) verschwinden diese Skalarprodukte für alle \(i \leq n-1\). Es bleibt nur der letzte Term in der Summe übrig:
Anwendung auf Modellproblem#
Wir wenden das Verfahren auf das Modellproblem
an.
from ngsolve import *
from netgen.geom2d import unit_square
from ngsolve.webgui import Draw
import matplotlib.pyplot as plt
from myst_nb import glue
import numpy as np
import matplotlib.pyplot as plt
from numpy.linalg import norm
Diskretierung der schwachen Gleichung mit FEM 1. Ordnung:
mesh = Mesh(unit_square.GenerateMesh(maxh=0.1))
V = H1(mesh, order=1, dirichlet='bottom|right|top|left')
u = V.TrialFunction()
v = V.TestFunction()
a = BilinearForm(grad(u)*grad(v)*dx+10*u*v*dx).Assemble()
f = LinearForm(1*v*dx).Assemble()
gfu = GridFunction(V)
Die Reduktion der Freiheitsgrade können wir in dem Fall direkt im Vorkonditionierer einbauen:
pre = a.mat.CreateSmoother(freedofs = V.FreeDofs())
Damit folgt für das CG-Verfahren:
w = f.vec.CreateVector()
r = f.vec.CreateVector()
p = f.vec.CreateVector()
ap = f.vec.CreateVector()
r.data = f.vec
p.data = pre*r
pi = f.vec.CreateVector()
pi.data = p
KrylovSpace = [pi]
wrn = InnerProduct(r,p)
err0 = sqrt(wrn)
errs = []
gfu.vec[:] = 0
maxit=200
tol=1e-8
its = 0
while True:
ap.data = a.mat * p
pap = InnerProduct(p, ap)
wr = wrn
alpha = wr / pap
gfu.vec.data += alpha * p
r.data -= alpha * ap
w.data = pre*r
wrn = InnerProduct(w, r)
err = sqrt(wrn)
errs.append(err)
#print ("Iteration",it,"err=",err)
if err < tol * err0 or its > 10000: break
beta = wrn / wr
p *= beta
p.data += w
pi = f.vec.CreateVector()
pi.data = p
KrylovSpace.append(pi)
its += 1
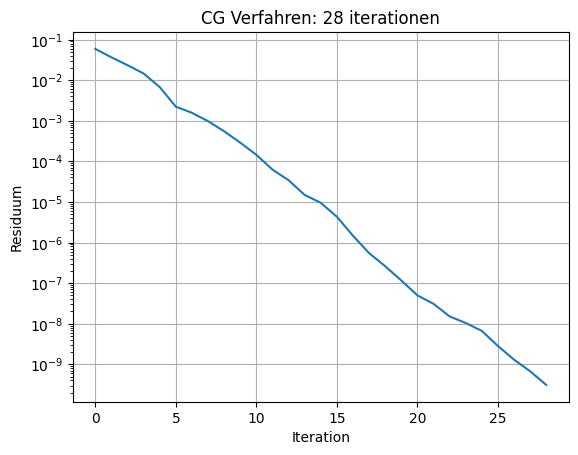
print ("needed", its, "iterations")
needed 28 iterations
fig, ax = plt.subplots()
ax.semilogy(errs)
ax.grid()
ax.set_title('CG Verfahren: '+str(its)+' iterationen')
ax.set_xlabel('Iteration')
ax.set_ylabel('Residuum')
#plt.savefig('FEM_CGVerfahren_fig.png')
glue("FEM_CGVerfahren_fig", fig, display=False)
Draw(gfu,mesh,'u');
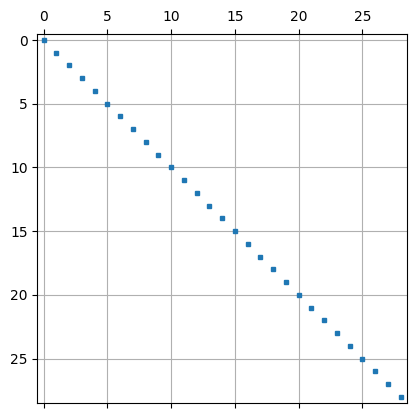
\(A\) Orthogonalität der Krylov Basis Funktionen (Vektoren)
orthoKrylov = np.array([[KrylovSpace[i].InnerProduct(a.mat*KrylovSpace[j])
for i in range(len(KrylovSpace))]
for j in range(len(KrylovSpace))])
orthoKrylov *= 1/np.diag(orthoKrylov)
plt.spy(orthoKrylov,precision=1e-2,markersize=3)
plt.grid()
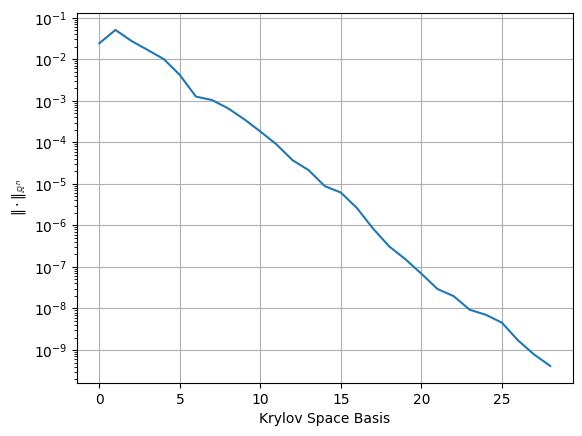
plt.semilogy([k.Norm() for k in KrylovSpace])
plt.xlabel('Krylov Space Basis')
plt.ylabel('$\|\cdot\|_{\mathbb{R}^n}$')
plt.grid()
plt.show()
gfu.vec.data = KrylovSpace[0]
Draw(gfu);
Vergleich CG - Gradienten Verfahren#
Lineares Gleichungssystem im \(\mathbb{R}^2\)
A = np.array([[3,-2],[-2,4]],dtype=np.float64)
b = np.array([7,-10],dtype=np.float64)
sol = np.array([1,-2])
A muss symmetrisch und positiv definit sein.
ews, evs = np.linalg.eig(A)
ews
array([1.43844719, 5.56155281])
Ritz Funktional ist gegeben durch
def f(x):
return 0.5*x@(A@x)-b@x
rp = np.linspace(0,2,40)
phip = np.linspace(0,2*np.pi,40)
Rp,Phip = np.meshgrid(rp,phip)
Xp = Rp.flatten()*np.sqrt(ews[0])*np.cos(Phip.flatten())
Yp = Rp.flatten()*np.sqrt(ews[1])*np.sin(Phip.flatten())
phi0 = np.arctan2(-evs[1,1],-evs[0,1])
rotmat = np.array([[np.cos(phi0),-np.sin(phi0)],[np.sin(phi0),np.cos(phi0)]])
XYvec = np.array([rotmat@xyp for xyp in np.array([Xp,Yp]).T])+sol
Xp = np.reshape(XYvec[:,0], Rp.shape)
Yp = np.reshape(XYvec[:,1], Rp.shape)
Zp = np.array([[f(np.array([Xp[i,j],Yp[i,j]]))
for j in range(len(rp))] for i in range(len(phip))])
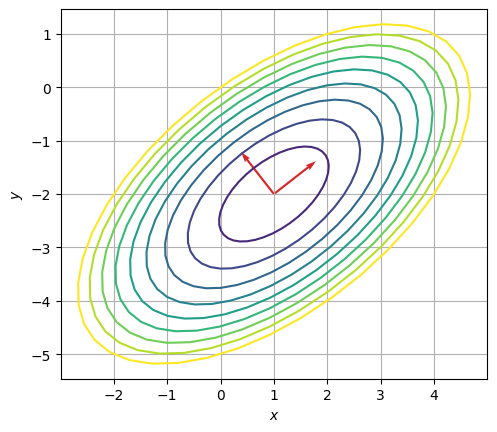
plt.contour(Xp,Yp,Zp, np.linspace(-14,0,10))
plt.quiver(np.ones(2),-2*np.ones(2),-evs[0,:],-evs[1,:],
angles='xy',scale=1,scale_units='xy', color='tab:red',
label='Eigen System', width=.005)
plt.grid()
plt.gca().set_aspect(1)
plt.xlabel(r'$x$')
plt.ylabel(r'$y$')
plt.show()
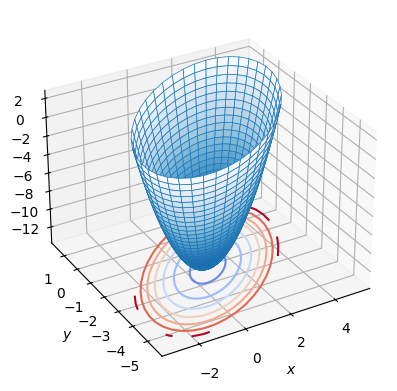
ax = plt.figure().add_subplot(projection='3d')
ax.plot_surface(Xp, Yp, Zp, linewidth=1, alpha=1, edgecolor='tab:blue' ,lw=0.5,
cmap=plt.cm.Blues_r,)
ax.contour(Xp, Yp, Zp, zdir='z', offset=-14, cmap='coolwarm')
ax.set_xlabel(r'$x$')
ax.set_ylabel(r'$y$')
ax.view_init(30, -120, 0)
plt.show()
Startwert für Gradienten und CG-Verfahren
x0 = np.array([-0.5,-5])
#x0 = np.array([0,-5])
Gradienten Verfahren#
# timeit ohne print verwenden.
sol = np.array(x0,dtype=np.float64)
xG = [np.array(sol)]
r = b-A@sol
err0 = np.linalg.norm(r)
its = 0
while True:
p = A @ r
err2 = np.dot(r,r)
err = np.sqrt(err2)
alpha = err2 / np.dot(r,p)
print ("iteration", its, "res=", err)
sol += alpha * r
xG.append(np.array(sol))
r -= alpha * p
if np.sqrt(err2) < 1e-8 * err0 or its > 10000: break
its += 1
print ("needed", its, "iterations")
xG = np.array(xG)
iteration 0 res= 9.12414379544733
iteration 1 res= 3.4148842275358424
iteration 2 res= 2.4835521654806128
iteration 3 res= 0.9295165999459604
iteration 4 res= 0.6760120726879713
iteration 5 res= 0.2530103663861413
iteration 6 res= 0.184007539189921
iteration 7 res= 0.06886831876113994
iteration 8 res= 0.050086050008101776
iteration 9 res= 0.018745656143383114
iteration 10 res= 0.013633204467914993
iteration 11 res= 0.005102485882728416
iteration 12 res= 0.003710898823802484
iteration 13 res= 0.0013888744135868948
iteration 14 res= 0.0010100904826086505
iteration 15 res= 0.00037804556074241916
iteration 16 res= 0.00027494222599448666
iteration 17 res= 0.00010290235358857979
iteration 18 res= 7.483807533714893e-05
iteration 19 res= 2.800957205600896e-05
iteration 20 res= 2.0370597858915606e-05
iteration 21 res= 7.624083409184791e-06
iteration 22 res= 5.544787933952574e-06
iteration 23 res= 2.0752422676781593e-06
iteration 24 res= 1.5092671037659337e-06
iteration 25 res= 5.648718984854972e-07
iteration 26 res= 4.1081592617127055e-07
iteration 27 res= 1.5375566827462807e-07
iteration 28 res= 1.1182230419972947e-07
iteration 29 res= 4.1851622624460305e-08
needed 29 iterations
plt.contour(Xp,Yp,Zp, np.linspace(-14,0,7),linestyles='--',linewidths=1)
plt.contour(Xp,Yp,Zp,np.array([f(xi) for xi in xG])[:10][::-1])
plt.plot(*xG.T,'.-',label='Gradienten Verfahren')
plt.quiver(np.ones(2),-2*np.ones(2),-evs[0,:],-evs[1,:],
angles='xy',scale=1,scale_units='xy', color='tab:red',
label='Eigen System', width=.005)
plt.grid()
plt.gca().set_aspect(1)
plt.xlabel(r'$x$')
plt.ylabel(r'$y$')
plt.show()
CG-Verfahren#
# timeit ohne print verwenden.
x = np.array(x0,dtype = np.float64)
r = b-A@x
p = np.array(r)
# speichern der Basis
pi = [np.array(p)]
wrn = r@p
xCG = [np.array(x)]
err0 = np.linalg.norm(r)
its = 0
while True:
ap = A@p
pap = p@ap
wr = wrn
alpha = wr/pap
x += alpha*p
xCG.append(np.array(x))
r -= alpha*ap
w = np.array(r)
wrn = w@r
err = np.sqrt(wrn)
print ("iteration", its, "res=", err)
beta = wrn/wr
p *= beta
p += w
pi.append(np.array(p))
if np.sqrt(err) < 1e-8 * err0 or its > 10000: break
its += 1
pi = np.array(pi)
print ("needed", its, "iterations")
xCG = np.array(xCG)
iteration 0 res= 3.4148842275358424
iteration 1 res= 6.661338147750939e-16
needed 1 iterations
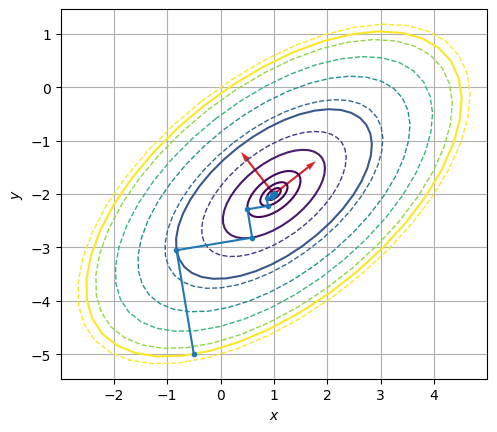
Aufgrund der Dimension des Problems, ist die Lösung in zwei Schritten exakt berechnet.
Vergleich#
xCG
array([[-0.5 , -5. ],
[-0.8245614 , -3.05263158],
[ 1. , -2. ]])
xG
array([[-0.5 , -5. ],
[-0.8245614 , -3.05263158],
[ 0.59170654, -2.81658692],
[ 0.50336234, -2.28652173],
[ 0.8888643 , -2.2222714 ],
[ 0.86481739, -2.07798997],
[ 0.96974935, -2.06050131],
[ 0.96320388, -2.02122853],
[ 0.9917659 , -2.01646819],
[ 0.98998426, -2.00577831],
[ 0.99775871, -2.00448257],
[ 0.99727376, -2.00157283],
[ 0.99938993, -2.00122014],
[ 0.99925793, -2.00042812],
[ 0.99983394, -2.00033212],
[ 0.99979801, -2.00011653],
[ 0.9999548 , -2.0000904 ],
[ 0.99994502, -2.00003172],
[ 0.9999877 , -2.00002461],
[ 0.99998503, -2.00000863],
[ 0.99999665, -2.0000067 ],
[ 0.99999593, -2.00000235],
[ 0.99999909, -2.00000182],
[ 0.99999889, -2.00000064],
[ 0.99999975, -2.0000005 ],
[ 0.9999997 , -2.00000017],
[ 0.99999993, -2.00000014],
[ 0.99999992, -2.00000005],
[ 0.99999998, -2.00000004],
[ 0.99999998, -2.00000001],
[ 0.99999999, -2.00000001]])
xCG[:,0]
array([-0.5 , -0.8245614, 1. ])
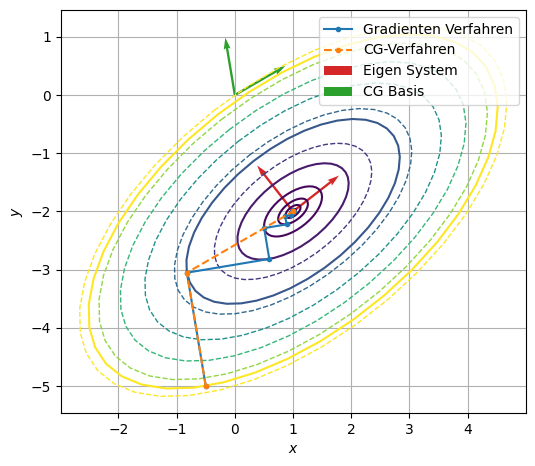
plt.figure(figsize=(6,6))
plt.contour(Xp,Yp,Zp, np.linspace(-14,0,7),linestyles='--',linewidths=1)
plt.contour(Xp,Yp,Zp,np.array([f(xi) for xi in xG])[:10][::-1])
plt.plot(*xG.T,'.-',label='Gradienten Verfahren')
plt.plot(*xCG.T,'.--',label='CG-Verfahren')
plt.quiver(np.ones(2),-2*np.ones(2),-evs[0,:],-evs[1,:],
angles='xy',scale=1,scale_units='xy', color='tab:red',
label='Eigen System', width=.005)
pin = norm(pi,axis=1)
plt.quiver(np.zeros(2),np.zeros(2),pi[:2,0]/pin[:2],pi[:2,1]/pin[:2],
angles='xy',scale=1,scale_units='xy', color='tab:green',
label='CG Basis', width=.005)
plt.gca().set_aspect(1)
plt.legend()
plt.grid()
plt.xlabel(r'$x$')
plt.ylabel(r'$y$')
plt.show()