Zweidimensionaler Fall

9.2.2. Zweidimensionaler Fall#

Eine reguläre Triangulierung \(\mathcal{T} = \{T_1, \ldots, T_M\}\) eines Gebiets \(\Omega\) ist die Zerlegung in Dreiecke \(T_i\) so, dass \(\bar{\Omega} = \cup_i T_i\) und \(T_i\cap T_j\) ist

entweder leer
oder hat eine gemeinsame Kante.

In einem erweiterten Sinne kann die Triangulierung aus verschiedenen Elemente bestehen: Dreiecke, Vierecke, (Tetraeder, Hexeder, Prismen, Pyramiden im dreidimensionalen). Die finite Elemente werden typischerweise, wie wir es im eindimensionalen gemacht haben, auf einem Referenzelement definiert. Die einzelnen Elemente der Zerlegung können mit Hilfe einer affinen Transformation und dem Referenzelement beschrieben werden.

Die Koordinaten Transformation im zweidimensionalen erfordert etwas mehr Rechenaufwand.

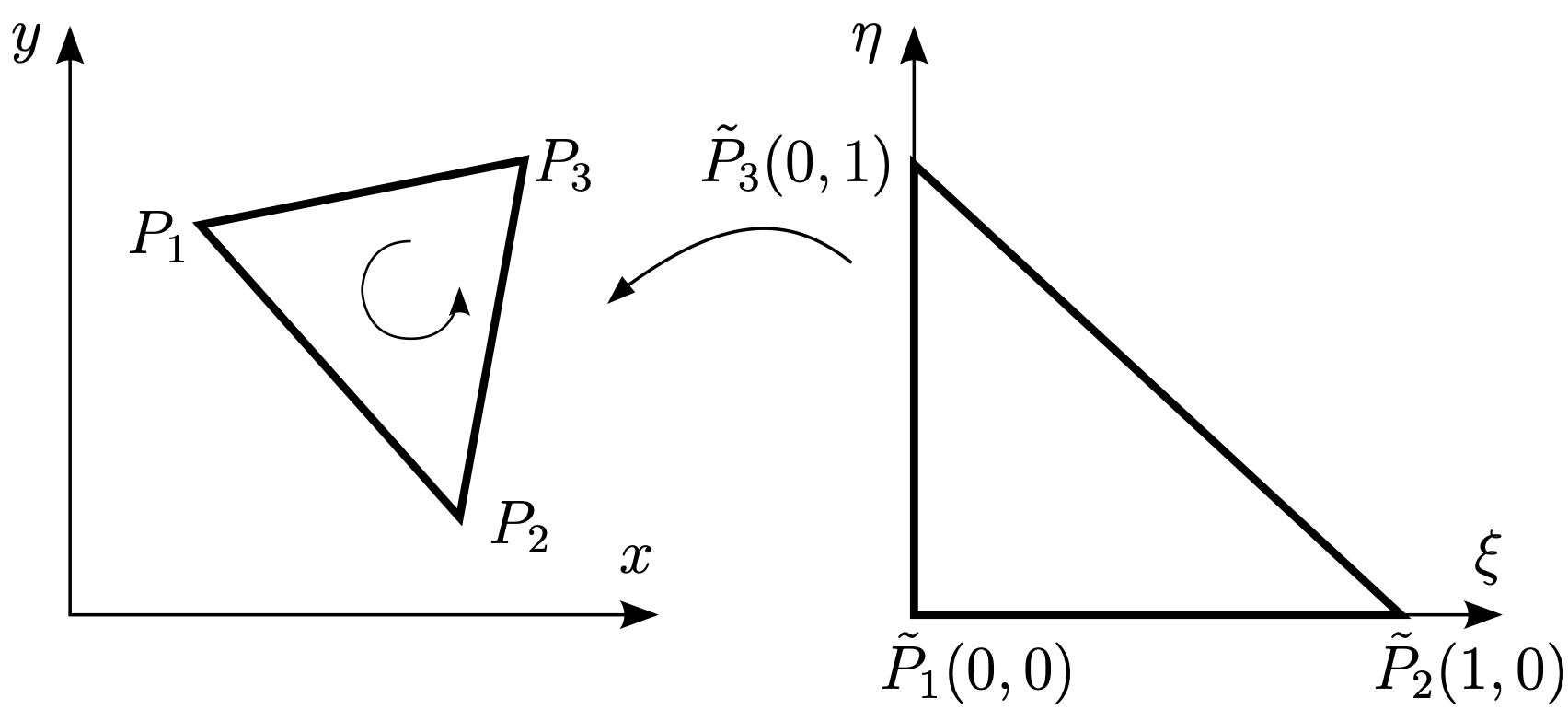
../_images/KoordinatenTransformation2d.png — Abb. 9.7 Transformation auf Einheitsdreieck in \(2D\)#

Ein Dreieck \(T_i\) in allgemeiner Lage mit den Eckpunkten \(P_1(x_1,y_1)\), \(P_2(x_2,y_2)\) und \(P_3(x_3,y_3)\), welche im Gegenuhrzeigersinn fortlaufend numeriert seien, wie dies in Abb. Abb. 9.7 erfolgte, kann mittels der linearen Transformation

\[\begin{split}\begin{split} x & = x_1 + (x_2-x_1)\, \xi + (x_3-x_1)\, \eta\\ y & = y_1 + (y_2-y_1)\, \xi + (y_3-y_1)\, \eta \end{split}\end{split}\]

bijektiv auf das Einheitsdreieck \(T\) abgebildet werden. Für das Dreieck \(T_i\) gegeben durch die drei Punkte \(\vec{p}_{i,1}, \vec{p}_{i,2}, \vec{p}_{i,3}\) definieren wir die Matrix

\[A_i = (\vec{p}_{i,2}-\vec{p}_{i,1},\ \vec{p}_{i,3}-\vec{p}_{i,1}) \in \mathbb{R}^{2\times 2}.\]

Damit können wir die Transformation wie folgt schreiben

\[\begin{split}\begin{array}{rl}\sigma_i : T & \to T_i\\ \vec{t} & \mapsto \begin{pmatrix}x\\ y\end{pmatrix} = \sigma_i(\xi,\eta) = \vec{p}_{i,1} + A_i\cdot \begin{pmatrix}\xi\\\eta\end{pmatrix}\end{array}\end{split}\]

bzw. die inverse Transformation

\[\begin{split}\begin{array}{rl}\sigma_i^{-1} : T_i & \to T\\ \vec{x} & \mapsto \begin{pmatrix}\xi\\ \eta\end{pmatrix} = \sigma_i^{-1}(x,y) = A_i^{-1}\cdot\left(\begin{pmatrix}x\\ y\end{pmatrix} - \vec{p}_{i,1}\right)\end{array} \end{split}\]

Das Flächenelement \(dx dy\) kann mit der Jacobi-Determinante \(J = \det A_i\) der Transformation durch \(dx\, dy = J\, d\xi\, d\eta\) ersetzt werden. Die Basisfunktion \(\varphi\) auf dem Element \(T_i\) kann (analog zum eindimensionalen Fall) mit Hilfe der Basisfunktion \(\tilde{\varphi}\) auf dem Referenzelement beschrieben werden. Es gilt

(9.9)#\[\varphi(\vec{x}) = \tilde{\varphi}(\sigma_i^{-1}(\vec{x})).\]

analog zu (9.7). Für die Jacobimatrix folgt mit Hilfe der Kettenregel

\[D\varphi(\vec{x}) = D\tilde{\varphi}(\sigma_i^{-1}(\vec{x}))\cdot \underbrace{D\sigma_i^{-1}(\vec{x})}_{=A_i^{-1}}\]

und damit für den Gradient

\[\nabla \varphi(\vec{x}) = D\varphi(\vec{x})^T = (D\tilde{\varphi}(\sigma_i^{-1}(\vec{x}))\cdot A_i^{-1})^T = {A_i^{-1}}^T\cdot \nabla \tilde{\varphi}(\sigma_i^{-1}(\vec{x})).\]

Für die Elementsteifigkeitsmatrix folgt somit

(9.10)#\[\int_{T_i} \nabla \varphi_j(\vec{x})\cdot \nabla \varphi_k(\vec{x}) dx dy = \int_{T} \nabla \tilde{\varphi}_j(\vec{t})\cdot C_i\cdot \nabla \tilde{\varphi}_k(\vec{t})\, J_i\, d\xi d\eta \quad \text{für}\ j,k = 0,1,\ldots, N_e\]

mit

\[C_i = {A_i^{-1}}\cdot {A_i^{-1}}^T\]

und für die Elementmassenmatrix

(9.11)#\[\int_{T_i} \varphi_j(\vec{x})\cdot \varphi_k(\vec{x}) dx dy = \int_{T} \tilde{\varphi}_j(\vec{t}) \tilde{\varphi}_k(\vec{t})\, J_i\, d\xi d\eta \quad \text{für}\ j,k = 0,1,\ldots, N_e.\]

Beispiel: Betrachten wir Basisfunktionen erster Ordnung

\[\begin{split}\begin{split} \tilde{\varphi}_0(\xi,\eta) & = 1-\xi-\eta\\ \tilde{\varphi}_1(\xi,\eta) & = \xi\\ \tilde{\varphi}_2(\xi,\eta) & = \eta\end{split}\end{split}\]

auf dem Einheitsdreieck, gegeben durch die Punkte \((0,0), (1,0), (0,1)\). In dem Fall gilt \(N_e = 2\).

# Basisfunktionen auf dem Referenzelement
def myshape(t, j):
    xi, eta = t
    if j == 0:
        return 1-xi-eta
    elif j == 1:
        return xi
    else:
        return eta

# Gradienten der Basisfunktionen auf dem Referenzelement
def Dmyshape(t, j):
    if j == 0:
        return np.array([-1,-1])
    elif j == 1:
        return np.array([1,0])
    else:
        return np.array([0,1])

Die inverse Jacobi-Matrix der Transformation ist gegeben durch

def invDsigma(p1,p2,p3):
    return np.linalg.inv(np.array([(p2-p1),(p3-p1)]).T)

Damit können wir für ein beliebiges Dreieck die Elementsteifigkeitsmatrix (9.10) wie folgt berechnen

# Berechnung der C_i Matrix und Jacobi Determinante
def CnJ(p1,p2,p3):
    A = np.array([(p2-p1),(p3-p1)]).T
    invA = np.linalg.inv(A)
    return invA@invA.T, np.linalg.det(A)

# Gebietsintegration über Einheitsdreieck
from scipy.integrate import dblquad
def quadT(f):
    return dblquad(f, 0, 1, 0, lambda x: 1-x)[0]

# Integration über Dreieck gegeben durch (1,1), (1.5,-1), (2,1.2)
Ci, Ji = CnJ(np.array([1,1]),np.array([1.5,-1]),np.array([2,1.2]))

Ai = np.array([[ quadT(lambda x,y: Dmyshape([x,y], j)@Ci@Dmyshape([x,y], k)*Ji)
           for k in range(3)] for j in range(3)])
Ai = DataFrame(Ai)
Ai.style.\
    apply(highlight_ortho).\
    set_table_attributes('style="font-size: 12px"')

	0	1	2
0	1.211905	-0.223810	-0.988095
1	-0.223810	0.247619	-0.023810
2	-0.988095	-0.023810	1.011905

Die Matrix \(C_i\) kann analytisch berechnet werden so, womit die Invertierung hinfällig wird. Für \(C_i\cdot J_i^2\) erhalten wir

\[\begin{split}\displaystyle \left[\begin{matrix}\left(p_{1 x} - p_{3 x}\right)^{2} + \left(p_{1 y} - p_{3 y}\right)^{2} & - \left(p_{1 x} - p_{2 x}\right) \left(p_{1 x} - p_{3 x}\right) - \left(p_{1 y} - p_{2 y}\right) \left(p_{1 y} - p_{3 y}\right)\\- \left(p_{1 x} - p_{2 x}\right) \left(p_{1 x} - p_{3 x}\right) - \left(p_{1 y} - p_{2 y}\right) \left(p_{1 y} - p_{3 y}\right) & \left(p_{1 x} - p_{2 x}\right)^{2} + \left(p_{1 y} - p_{2 y}\right)^{2}\end{matrix}\right]\end{split}\]

und damit

(9.12)#\[\begin{split}C_i = \frac{1}{J_i^2} \begin{pmatrix}a_i & -c_i\\ -c_i & b_i\end{pmatrix}\end{split}\]

mit

(9.13)#\[\begin{split}\begin{split} a_i & = \|\vec{p}_{i,3}-\vec{p}_{i,1}\|^2 = (p_{i,3,x}-p_{i,1,x})^2+(p_{i,3,y}-p_{i,1,y})^2\\ b_i & = \|\vec{p}_{i,2}-\vec{p}_{i,1}\|^2 = (p_{i,2,x}-p_{i,1,x})^2+(p_{i,2,y}-p_{i,1,y})^2\\ c_i & = (p_{i,2,x}-p_{i,1,x})(p_{i,3,x}-p_{i,1,x}) + (p_{i,2,y}-p_{i,1,y})(p_{i,3,y}-p_{i,1,y})\\ J_i & = (p_{i,2,x}-p_{i,1,x})(p_{i,3,y}-p_{i,1,y}) - (p_{i,3,x}-p_{i,1,x})(p_{i,2,y}-p_{i,1,y}). \end{split}\end{split}\]

Für die Elementmassenmatrix (9.11) folgt

Bi = np.array([[ quadT(lambda x,y: myshape([x,y], j)*myshape([x,y], k)*Ji)
           for k in range(3)] for j in range(3)])
Bi = DataFrame(Bi)
Bi.style.\
    apply(highlight_ortho).\
    set_table_attributes('style="font-size: 12px"')

	0	1	2
0	0.175000	0.087500	0.087500
1	0.087500	0.175000	0.087500
2	0.087500	0.087500	0.175000

Das Assembling des Gesamtsystems erfolgt mit dem Algorithmus Algorithm 9.1 und der Abbildung der Freiheitsgrade \(T\) analog zu (9.8) für den zweidimensionalen Fall

\[T: \{0,1,\ldots, n\} \times \{0,1,2\} \to \{0,1,\ldots, N\},\]

wobei \(N\) im Fall von Elemente erster Ordnung die Anzahl Knoten und \(n\) die Anzahl Elemente (Dreiecke).

Remark 9.2

Es erweist sich mathematisch wie auch Software technisch als bedeutend effizienter, die Berechnung der System Matrizen über die Triangulierung zu berechnen und die einzelnen Beiträge in der globalen Matrix aufzukummulieren. Diesen Prozess nennt man Assembling.

Allgemein können wir dies in der Form

\[A = \sum_{T \in \mathcal{T}} C_T A_T C_T^T\]

und

\[f = \sum_{T \in \mathcal{T}} C_T f_T\]

schreiben, wobei \(C_T\) die Verknüpfung zwischen lokalen und globalen Funktionen darstellt.