11.3.3. Gradienten Verfahren

Die Theorie folgt direkt dem iFEM Jupyter-Notebook, wobei wir für das Beispiel Dirichlet Randbedingungen implementieren.

Für das zu lösende lineare Gleichungssystem

\[A x = b\]

nehmen an, dass die Matrix \(A\) symmetrisch positiv definit ist. Sei die Funktion \(f\) gegeben durch

\[\begin{split}\begin{split} f : \mathbb{R}^n & \to \mathbb{R}\\ x & \mapsto f(x) = \displaystyle\frac{1}{2} x^T A x - b^T x.\end{split}\end{split}\]

Dann folgt für den Gradient und die Mess’sche Matrix

\[\begin{split}\begin{split} \nabla f(x) & = A x - b, \\ H f & = A. \end{split}\end{split}\]

Da \(A\) positiv definit ist, ist \(f\) konvex und es existiert ein eindeutiger Minimierer von

\[ \min_{x \in {\mathbb R}^n} f(x). \]

Dieser ist durch die Gleichung \(\nabla f = 0\) charakterisiert und somit Lösung des linearen System \(A x = b\). Damit ist das lineare Gleichungssystem äquivalent zum Minimierungsproblem.

Sei \(x^\ast\) der Minimierer von \(f\), dann gilt für beliebiges \(x\)

\[ f(x) = f(x^\ast) + \frac{1}{2} \| x - x^\ast \|_A^2, \]

was einfach durch Berechnung überprüft werden kann

\[\begin{split}\begin{split} f(x^\ast) + \frac{1}{2} \| x - x^\ast \|_A^2 & = \frac{1}{2} {x^\ast}^T A x^\ast - b^T x^\ast + \frac{1}{2}(x - x^\ast)^T A (x - x^\ast) \\ & = x^\ast A x^\ast - b^T x^\ast + \frac{1}{2} x^T A x - x^T A x^\ast \\ & = \frac{1}{2} x^T A x - b^T x = f(x). \end{split}\end{split}\]

Der Fehler in der Energie Norm \(\|\cdot\|_A\) steht damit in direktem Zusammenhang mit dem Abstand zum Minimum

\[f(x) - f(x^\ast) = \frac{1}{2} \| x - x^\ast \|_A^2.\]

Wenden wir nun die Gradientenmethode an: Die nächste Iteration \(x^{k+1}\) erhält man, indem man von \(x^k\) in die Richtung des negativen Gradienten geht:

\[\begin{split}\begin{split} x^{k+1} & = x^k - \alpha \nabla f(x^k) \\ & = x^k + \alpha\, r \qquad \text{mit} \qquad r = b - A x^k \end{split}\end{split}\]

Der optimale Parameter \(\alpha\) kann durch Zeilensuche ermittelt werden:

\[ \min_{\alpha \in {\mathbb R}} f(x^k + \alpha r) \]

daher

\[ \min_\alpha \frac{1}{2} (x^k + \alpha r)^T A (x^k + \alpha r) - b^T (x^k + \alpha r) \]

was auf ein Minimierungsproblem einer konvexen quadratischen Funktion in \(\alpha\) hinausläuft

\[ \min_{\alpha \in {\mathbb R}} \frac{1}{2} r^T A r \, \alpha^2 - (b-A x^k)^T r \, \alpha + \frac{1}{2} {x^k}^T A x^k - b^T x^k. \]

Der optimale Wert \(\alpha_\text{opt}\) ist gegeben durch

\[ \alpha_\text{opt} = \frac{r^T r}{r^T A r}. \]

Damit erhalten wir das Gradienten Verfahren:

Gegeben \(x^0\)
for \(k = 0, 1, 2, \ldots\)
\(\qquad r = b - A x^k\)
\(\qquad \alpha = \frac{r^T r}{r^T A r}\)
\(\qquad x^{k+1} = x^k + \alpha r\)

In dieser Version benötigt man zwei Matrix-Vektor-Produkte mit \(A\). Durch Aktualisierung des Residuums kann man das zweite Produkt vermeiden:

Algorithm 11.1 (Gradienten Verfahren)

Given \(x^0\)
\(r^0 = b - A x^0\)
for \(k = 0, 1, 2, \ldots\)
\(\qquad p = A r^k\)
\(\qquad \alpha = \frac{{r^k}^T r^k}{{r^k}^T p}\)
\(\qquad x^{k+1} = x^k + \alpha r^k\)
\(\qquad r^{k+1} = r^k - \alpha p\)

Anwendung auf Modellproblem

Wir wenden das Verfahren auf das Modellproblem

\[\begin{split}\begin{split} -\Delta u + 10\, u & = 1\quad x\in\Omega = [0,1]^2\\ u & = 0\quad x \in \partial\Omega\end{split}\end{split}\]

an.

from ngsolve import *
from netgen.geom2d import unit_square
from ngsolve.webgui import Draw
import matplotlib.pyplot as plt
from myst_nb import glue

Diskretierung der schwachen Gleichung mit FEM 1. Ordnung:

mesh = Mesh(unit_square.GenerateMesh(maxh=0.1))
V = H1(mesh, order=1, dirichlet='bottom|right|top|left')
u = V.TrialFunction()
v = V.TestFunction()
a = BilinearForm(grad(u)*grad(v)*dx+10*u*v*dx).Assemble()
f = LinearForm(1*v*dx).Assemble()
gfu = GridFunction(V)

Wir nutzen das CSR Modul von scipy um das reduzierte Problem für die freien Freiheitsgrade zu lösen.

import scipy.sparse as sp
import numpy as np
from numpy.linalg import norm

Das auf die freien Freiheitsgrade reduzierte Systemmatrix kann wie folgt berechnet werden:

rows,cols,vals = a.mat.COO()
ind = np.arange(V.ndof)[np.array(V.FreeDofs())]

# Reduktion auf die freien Freiheitsgrade der Systemmatrix
A = sp.csr_matrix((vals,(rows,cols)))
A = A[np.ix_(ind,ind)]
# Reduktion auf die freien Freiheitsgrade der rechten Seite
fd = np.array(f.vec)[ind]

Für das Gradienten Verfahren folgt somit

sol = np.zeros(V.ndof)
r = np.array(fd)
err0 = norm(r)
errs = []
its = 0
while True:
    p = A @ r
    err2 = np.dot(r,r)
    err = sqrt(err2)
    errs.append(err)
    alpha = err2 / np.dot(r,p)
    
    #print ("iteration", its, "res=", err)
    sol[ind] += alpha * r
    r -= alpha * p
    if err < 1e-8 * err0 or its > 10000: break
    its += 1
print ("needed", its, "iterations")

needed 190 iterations

fig, ax = plt.subplots()
ax.loglog(errs)
ax.grid()
ax.set_title('Gradienten Verfahren: '+str(its)+' iterationen')
ax.set_xlabel('Iteration')
ax.set_ylabel('Residuum')
#plt.savefig('FEM_GradientenVerfahren_fig.png')
glue("FEM_GradientenVerfahren_fig", fig, display=False)

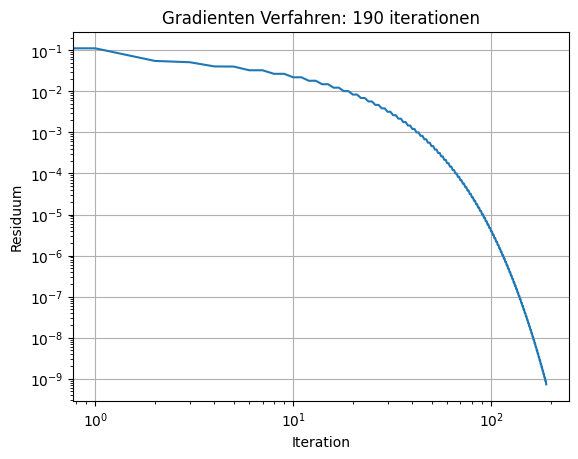
Es ist zu sehen, dass die Gradientenmethode ähnlich schnell wie die Richardson-Iteration konvergiert, jedoch ohne die Notwendigkeit eines gut gewählten Relaxationsparameters \(\alpha\).

Der Vergleich mit der Richardson-Iteration erlaubt es auch, die Fehlerreduktion der Gradientenmethode abzuschätzen. Sei

\[ \tilde x^{k+1} = x^k - \alpha_\text{Rich} (b - A x^k) \]

ein Schritt des Richardson Verfahren. Dann gilt

\[ \| x^{k+1} - x^\ast \|_A^2 = 2 \, (f(x^{k+1}) - f(x^\ast)) \leq 2 \, ( f (\tilde x^{k+1}) - f(x^\ast) ) = \| \tilde x^{k+1} - x^\ast \|_A^2 \]

Ein Schritt der Gradientenmethode reduziert den Fehler (gemessen in der Energienorm) mindestens so stark wie ein Schritt der Richardson-Methode.

gfu.vec[:] = sol
Draw(gfu,mesh,'u')

BaseWebGuiScene